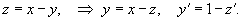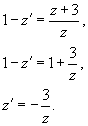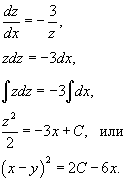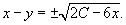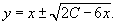|
|
|
|
Однородные уравнения
|
|
Определение однородного дифференциального уравнения
Дифференциальное уравнение первого порядка
называется однородным, если правая часть удовлетворяет соотношению
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
Однородное дифференциальное уравнение можно также записать в виде
или через дифференциалы:
где P(x,y) и Q(x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
|
|
Пример 1
|
|
Решить дифференциальное уравнение 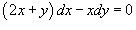 .
Решение.
Нетрудно заметить, что многочлены P(x,y) и Q(x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным.
Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда
Подставляя это в дифференциальное уравнение, получаем
Следовательно,
Разделим обе части уравнения на x:
Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0 действительно является одним из решений нашего уравнения.
Интегрируем последнее выражение:
где C − постоянная интегрирования.
Возвращаясь к старой переменной y, можно записать:
Таким образом, уравнение имеет два решения:
|
|
Пример 2
|
|
Решить дифференциальное уравнение 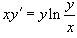 .
Решение.
Заметим, что корень x = 0 не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме:
Как видно, уравнение является однородным.
Сделаем замену y = ux. Следовательно,
Подставляем полученное выражение в дифференциальное уравнение:
Разделим обе части на x ≠ 0:
В результате мы получаем уравнение с разделяющимися переменными:
На следующем шаге проинтегрируем левую и правую части уравнения:
Следовательно,
Постоянную C здесь можно записать как ln C1 (C1 > 0). Тогда
Таким образом, мы получили два решения:
Если C1 = 0, то ответом является функция y = xe. Легко убедиться, что эта функция будет также и решением дифференциального уравнения. В самом деле, подставляя
в дифференциальное уравнение, находим:
Таким образом, все решения дифференциального уравнения можно представить одной формулой:
где C − произвольное действительное число.
|
|
Пример 3
|
|
Решить дифференциальное уравнение 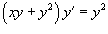 .
Решение.
Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде:
Сделаем подстановку y = ux. Тогда y' = u'x + u. Подставляя y и y' в исходное уравнение, получаем:
Разделим обе части уравнения на ux2. Заметим, что корень x =0 не является решением, но можно убедиться, что корень u = 0 (или y = 0) будет одним из решений данного дифференциального уравнения.
В результате получаем:
Интегрируя, находим общее решение:
Учитывая, что 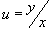 , последнее выражение можно записать в форме
Обратная функция x(y) имеет явный вид:
Поскольку C − произвольное число, знак "минус" перед этой константой можно заменить на знак "плюс". Тогда получаем:
Таким образом, дифференциальное уравнение имеет решения:
|
|
Пример 4
|
|
Решить дифференциальное уравнение 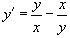 .
Решение.
Из вида правой части уравнения следует, что x ≠ 0 и y ≠ 0. Можно сделать подстановку: y = ux, y' = u'x + u, которая приводит к уравнению с разделяющимися переменными:
Интегрируя данное уравнение, получаем:
Переобозначим 2 C просто как постоянную C. Следовательно,
Итак, общее решение записывается в виде:
|
|
Пример 5
|
|
Найти общее решение дифференциального уравнения 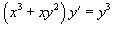 .
Решение.
Как видно, данное уравнение является однородным. Поэтому, воспользуемся подстановкой y = ux, y' = u'x + u. В результате уравнение преобразуется в уравнение с разделяющимися переменными:
Разделим обе части на x3. (Заметим, что корень x = 0 не является решением).
Теперь можно проинтегрировать последнее уравнение:
Так как u = y/x, то решение записывается в виде:
Отсюда следует, что
Переобозначим для краткости: eC = C1, (C1 > 0). Тогда решение в неявной форме определяется уравнением:
где постоянная C1 > 0.
|
|
Пример 6
|
|
Решить уравнение 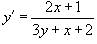 .
Решение.
Видно, что числитель и знаменатель в правой части соответствуют пересекающимся прямым. Поэтому данное дифференциальное уравнение можно преобразовать в однородное путем соответствующего преобразования координат. Пусть новые и старые координаты связаны соотношениями:
Константы α и β мы определим позже. Подставляя указанные соотношения в уравнение, получаем:
В новых координатах дифференциальное уравнение принимает вид:
Данное уравнение будет однородным, если коэффициенты α и β будут удовлетворять системе уравнений
Решая данную систему уравнений относительно α и β, находим:
При указанных значениях α и β дифференциальное уравнение записывается следующим образом:
Мы получили однородное уравнение. Далее делаем замену: Y = uX, где u − некоторая функция X. Следовательн, dY = Xdu + udX. В итоге мы имеем:
Разделим числитель и знаменатель в правой части на X. Можно проверить, что X = 0 или x = X + α = −1/2 не является решением дифференциального уравнения.
Простые преобразования приводят к следующему результату:
Разложим квадратичную функцию в числителе дроби в правой части на произведение одночленов:
Следовательно,
Тогда
Разделяя переменные, можно записать:
Интегрируем полученное уравнение:
Теперь преобразуем подынтегральное выражение в левой части. Воспользуемся методом неопределенных коэффициентов и разложим подынтегральное выражение на сумму рациональных дробей:
Следовательно,
Таким образом, дифференциальное уравнение записывается в следующем виде:
После интегрирования обеих частей получаем:
где постоянная C является положительным действительным числом.
Перепишем решение через переменные X и Y:
Далее удобно обозначить: 5lnC = lnC1, где C1 − произвольное положительное число. Таким образом, решение можно записать в виде:
Теперь мы можем вернуться к первоначальным переменным x,y. Так как
то получаем:
Правую часть можно снова несколько упростить:
Тогда окончательное общее решение исходного дифференциального уравнения выражается следующей неявной формулой:
где постоянная C3 − любое число, не равное нулю.
|
|
Пример 7
|
|
Найти общее решение дифференциального уравнения 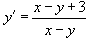 .
Решение.
Можно заметить, что уравнения прямых в числителе и знаменателе в правой части соответствуют параллельным прямым. Поэтому, сделаем следующую замену переменных:
В результате дифференциальное уравнение принимает вид:
Как видно, мы получили простое уравнение с разделяющимися переменными. Решая его, находим ответ:
Из последнего выражения можно вывести явную функцию y(x):
Таким образом,
|
|
|
|
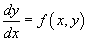
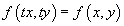
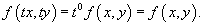
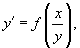
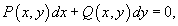
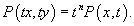
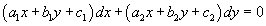
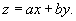
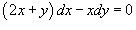 .
.
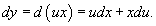
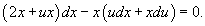
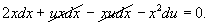
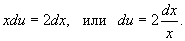
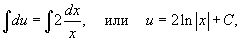
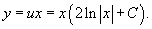
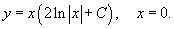
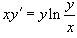 .
.
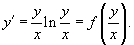
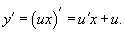
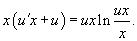
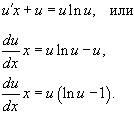
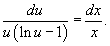
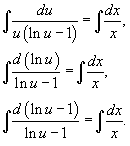
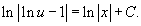
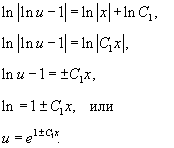
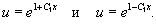
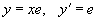
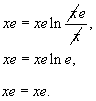
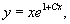
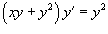 .
.
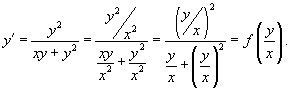
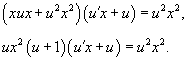
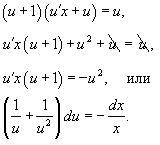
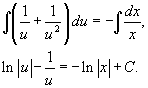
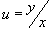 , последнее выражение можно записать в форме
, последнее выражение можно записать в форме
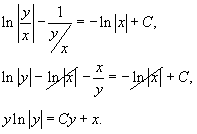
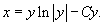
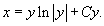
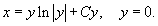
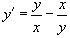 .
.
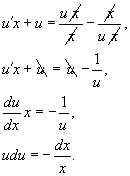
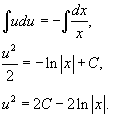
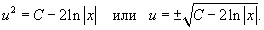
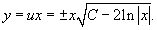
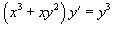 .
.
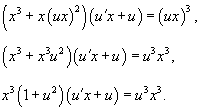
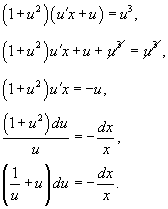
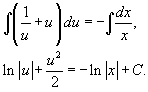
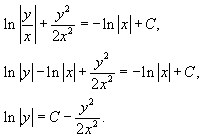
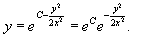
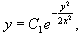
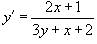 .
.
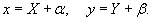
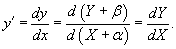
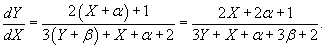
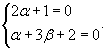
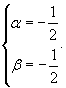
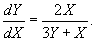
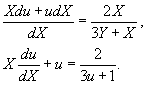
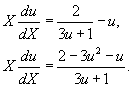
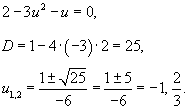
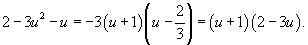
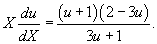
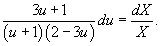
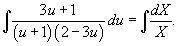
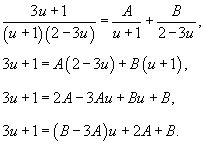
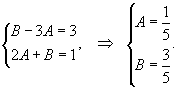
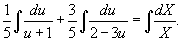
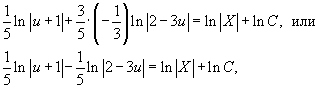
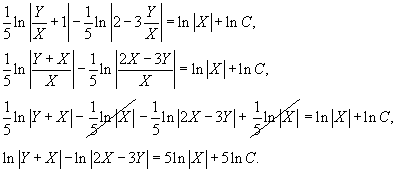
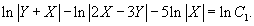
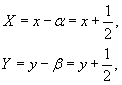
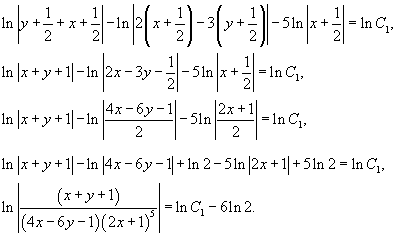
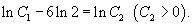
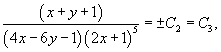
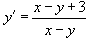 .
.