|
Геометрическая прогрессия
|
|
Последовательность чисел
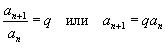 для всех членов геометрической прогрессии. Предполагается, что для всех членов геометрической прогрессии. Предполагается, что Любой член геометрической прогрессии можно вычислить по формуле: 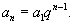 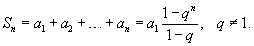 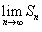 существует и конечен. существует и конечен.В противном случае прогрессия расходится. Пусть 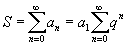 представляет собой бесконечный ряд геометрической прогрессии. Данный ряд сходится к представляет собой бесконечный ряд геометрической прогрессии. Данный ряд сходится к 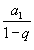 , если знаменатель , если знаменатель |
|
Пример 1
|
|
Найти сумму первых 8 членов геометрической прогрессии 3, 6, 12, ...
Решение. 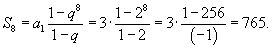 |
|
Пример 2
|
|
Найти сумму ряда
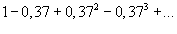 . .
Решение. 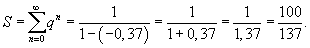 |
|
Пример 3
|
|
Найти сумму ряда
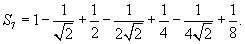 Решение. 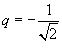 . Поскольку сумма геометрической прогрессии выражается формулой . Поскольку сумма геометрической прогрессии выражается формулой
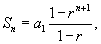 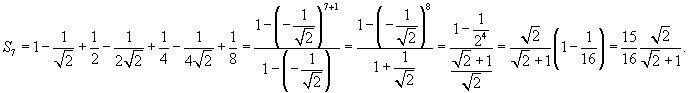 |
|
Пример 4
|
|
Выразить бесконечную периодическую дробь 0,131313... рациональным числом.
Решение. 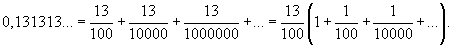 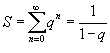 со знаменателем со знаменателем 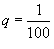 , получаем , получаем
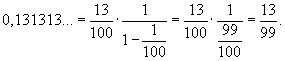 |
|
Пример 5
|
|
Показать, что
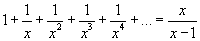 Решение. 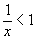 . Тогда левая часть в заданном выражении представляет собой сумму бесконечно убывающей геометрической прогрессии. Используя формулу . Тогда левая часть в заданном выражении представляет собой сумму бесконечно убывающей геометрической прогрессии. Используя формулу 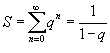 , левую часть можно записать в виде , левую часть можно записать в виде
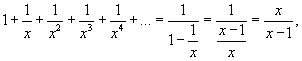 |
|
Пример 6
|
|
Решить уравнение
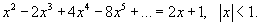 Решение. 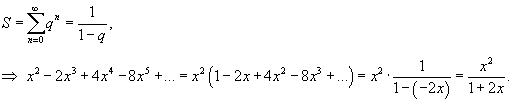 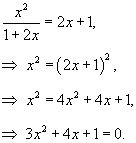 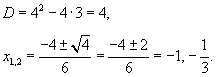 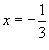 . . |
|
Пример 7
|
|
Известно, что второй член бесконечно убывающей геометрической прогрессии
Решение. 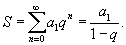 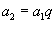 , то получаем следующую систему уравнений для определения a1 и q: , то получаем следующую систему уравнений для определения a1 и q:
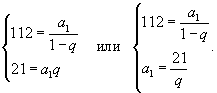 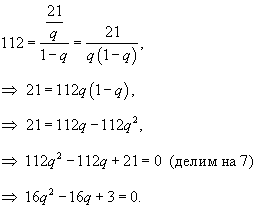 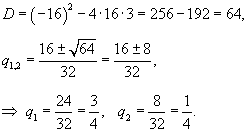 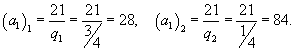 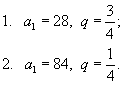 |