|
Геометрические приложения поверхностных интегралов
|
||||||
|
С помощью поверхностных интегралов вычисляются
Площадь поверхности
Пусть S является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности определяется интегралом
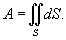 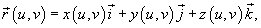 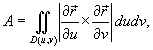 Если поверхность S задана в явном виде функцией 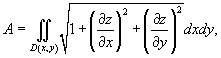
Объем тела, ограниченного замкнутой поверхностью
Предположим, что тело ограничено некоторой гладкой, замкнутой поверхностью S. Тогда объем тела определяется по формуле
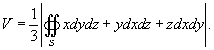 |
||||||
|
Пример 1
|
||||||
|
Вычислить площадь поверхности части параболоида
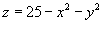 , лежащей выше плоскости xy. , лежащей выше плоскости xy.
Решение. 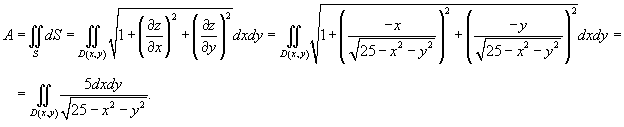 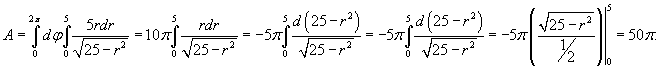 |
||||||
|
Пример 2
|
||||||
|
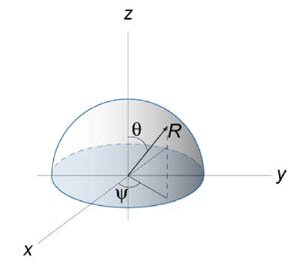
Найти площадь полусферы радиуса R.
Решение. 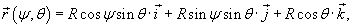 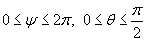 (рисунок 1). (рисунок 1).Вычислим дифференциальный элемент площади. 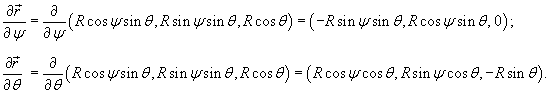 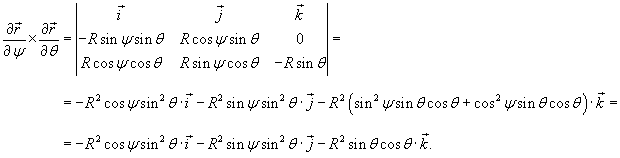 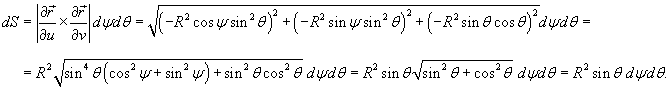 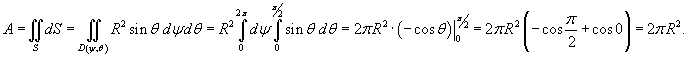
|
||||||
|
Пример 3
|
||||||
|
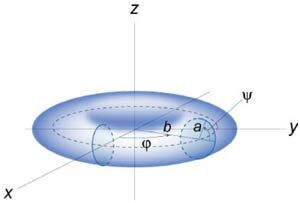
Вычислить площадь поверхности тора, заданного уравнением
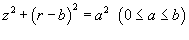 в цилиндрических координатах. в цилиндрических координатах.
Решение. 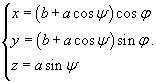 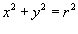 , то после подстановки получаем , то после подстановки получаем
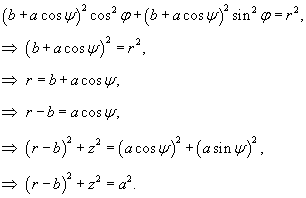 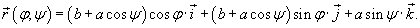 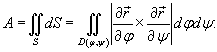 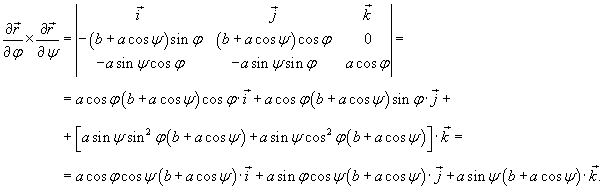 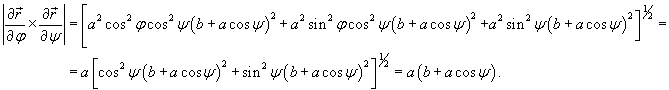 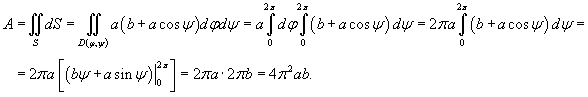 |
||||||
|
Пример 4
|
||||||
|
Вычислить объем эллипсоида
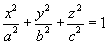 . .
Решение. 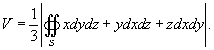 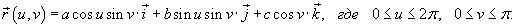 В формуле для объема векторное поле имеет координаты 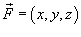 , поэтому , поэтому
 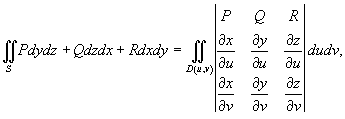  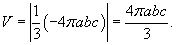 |
||||||