|
Геометрические приложения криволинейных интегралов
|
||||||
|
Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 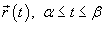 . Длина данной кривой выражается следующим криволинейным интегралом . Длина данной кривой выражается следующим криволинейным интегралом
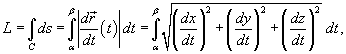 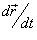 − производная, а − производная, а 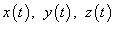 − компоненты векторной функции − компоненты векторной функции 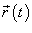 . .Если кривая C задана в плоскости, то ее длина выражается формулой 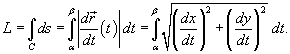 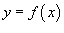 в плоскости Oxy, то длина такой кривой вычисляется по формуле в плоскости Oxy, то длина такой кривой вычисляется по формуле
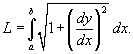 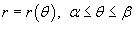 , и функция , и функция 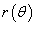 является непрерывной и дифференцируемой в интервале является непрерывной и дифференцируемой в интервале 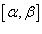 , то длина кривой определяется выражением , то длина кривой определяется выражением

Площадь области, ограниченной замкнутой кривой
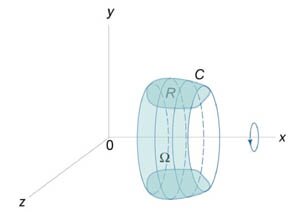
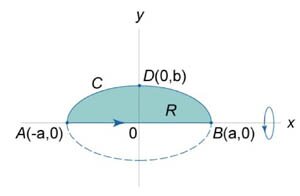
Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости Oxy (рисунок 1). Тогда площадь области R, ограниченной данной кривой, определяется формулами
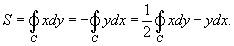 Если замкнутая кривая C задана в параметрическом виде 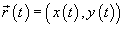 , то площадь соответствуюшей области равна , то площадь соответствуюшей области равна
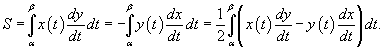
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
Предположим, что область R расположена в верхней полуплоскости 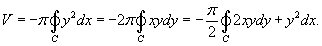 |
||||||
|
Пример 1
|
||||||
|
Найти длину кривой
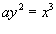 при условии при условии 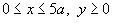 . .
Решение. 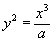 или или  . Поскольку . Поскольку 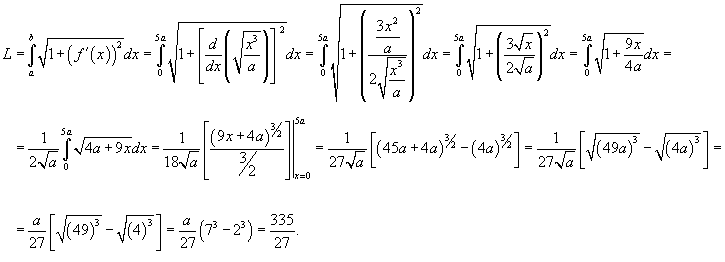
|
||||||
|
Пример 2
|
||||||
|
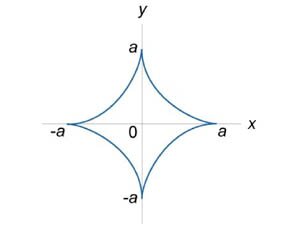
Вычислить длину астроиды
 . .
Решение. 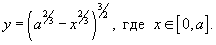 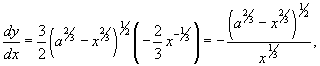 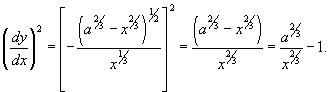 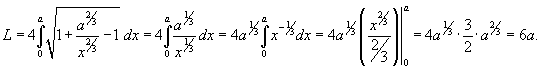 |
||||||
|
Пример 3
|
||||||
|
Найти длину пространственной кривой, заданной параметрически в виде
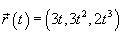 , где , где 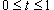 . .
Решение. 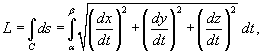 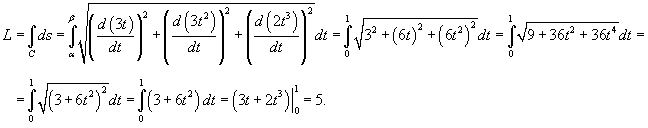 |
||||||
|
Пример 4
|
||||||
|
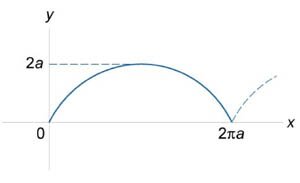
Найти длину циклоиды, заданной в параметрическом фиде вектором
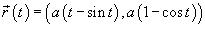 в интервале в интервале 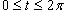 (рисунок 5). (рисунок 5).
Решение. 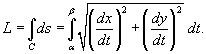 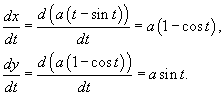 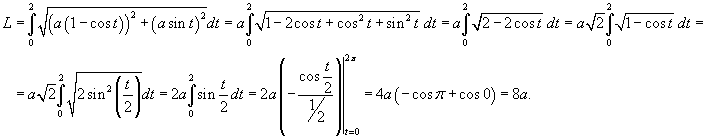
|
||||||
|
Пример 5
|
||||||
|
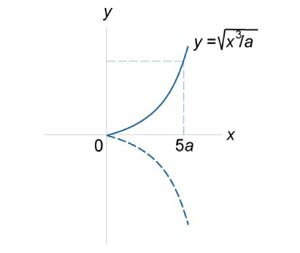
Вычислить длину параболы
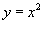 в интервале в интервале 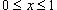 . .
Решение. 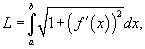 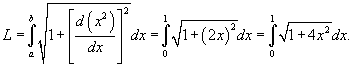 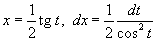 . Следовательно, . Следовательно, 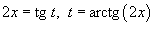 . При . При 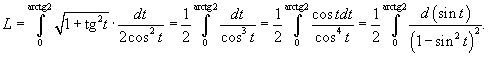 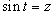 . Если . Если 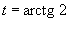 , то , то
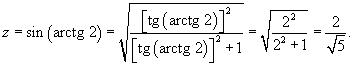 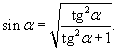 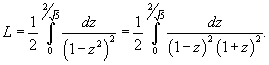 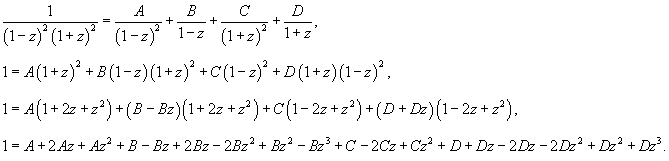 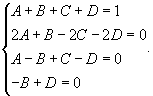 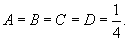 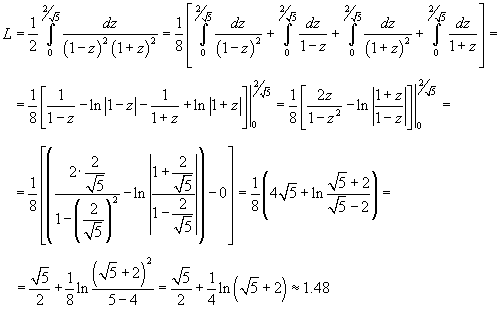 |
||||||
|
Пример 6
|
||||||
|
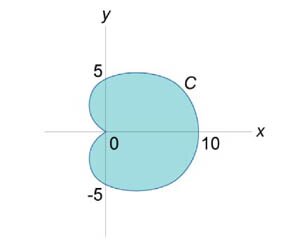
Найти длину кардиоиды, заданной в полярных координатах уравнением
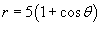 (рисунок 6). (рисунок 6).
Решение. 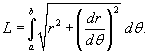 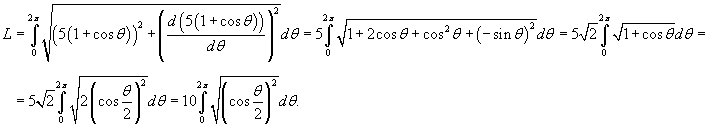 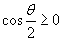 при при 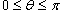 , и , и 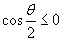 при при 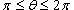 . Следовательно, . Следовательно,
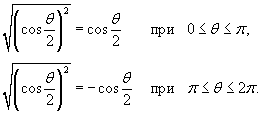 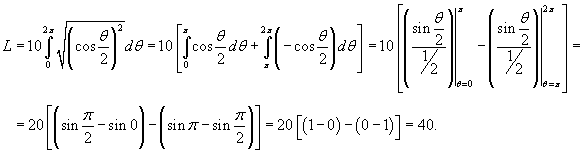
|
||||||
|
Пример 7
|
||||||
|
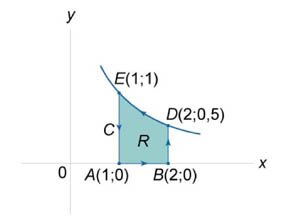
Найти площадь области, ограниченной гиперболой
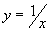 , осью Ox и вертикальными прямыми , осью Ox и вертикальными прямыми Решение. 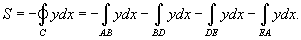 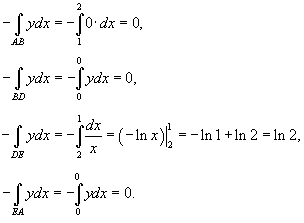 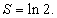 |
||||||
|
Пример 8
|
||||||
|
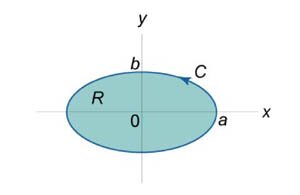
Найти площадь области, ограниченной эллипсом, заданным параметрически в виде
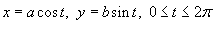 (рисунок 8). (рисунок 8).
Решение. 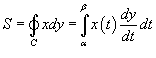 . Получаем . Получаем
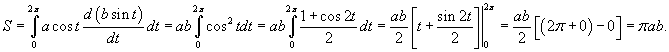 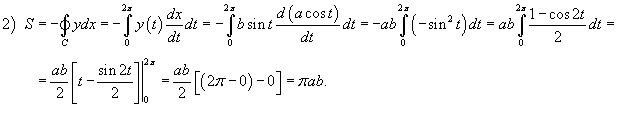 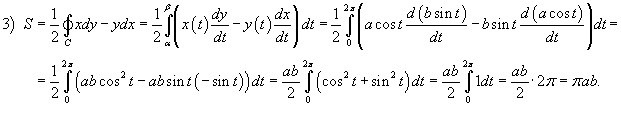
|
||||||
|
Пример 9
|
||||||
|
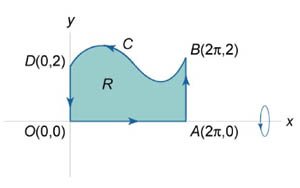
Найти объем тела, образованного вращением вокруг оси Ox области R, ограниченной кривой
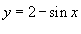 , и прямыми , и прямыми Решение. 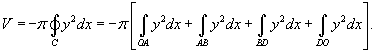 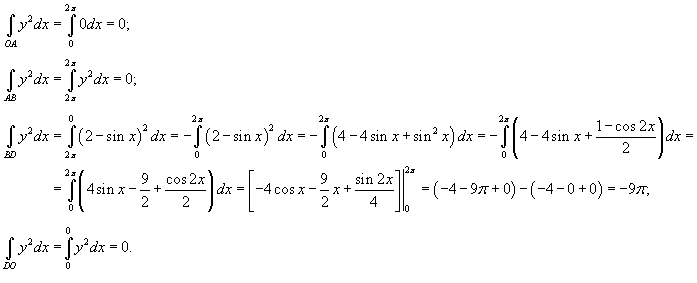 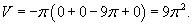 |
||||||
|
Пример 10
|
||||||
|
Найти объем эллипсоида, образованного вращением эллипса с полуосями a и b вокруг оси Оx. (рисунок 10).
Решение. 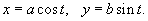 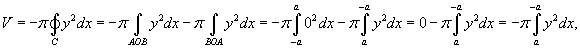 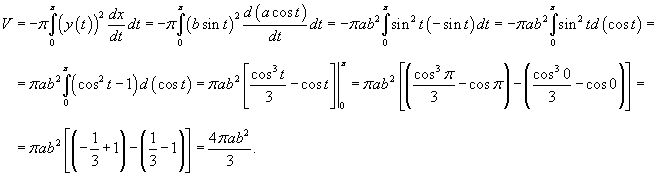 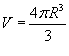 . .
|
||||||