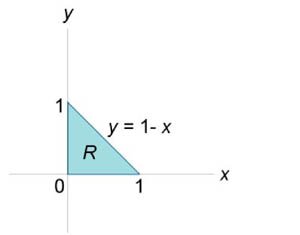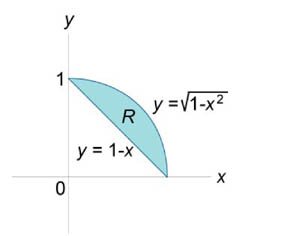|
Геометрические приложения двойных интегралов
|
||||||||||||
|
Площадь плоской фигуры
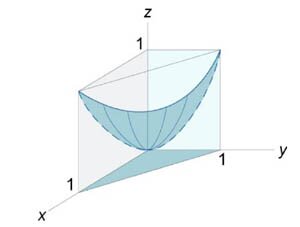
Если 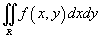 , то двойной интеграл равен площади области интегрирования R. , то двойной интеграл равен площади области интегрирования R.Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде 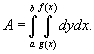 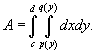
Объем тела
Если 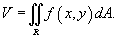 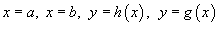 , объем тела равен , объем тела равен
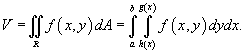 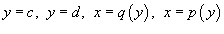 , объем соответственно равен , объем соответственно равен
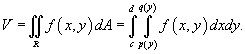 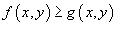 , то объем цилиндрического тела между поверхностями , то объем цилиндрического тела между поверхностями 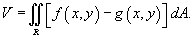
Площадь поверхности
Предположим, что поверхность задана функцией 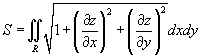 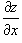 и и 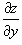 непрерывны всюду в области R. непрерывны всюду в области R.
Площадь и объем в полярных координатах
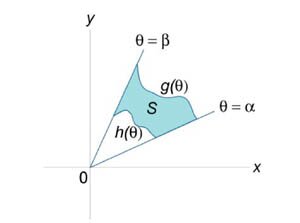
Пусть S является областью, ограниченной линиями 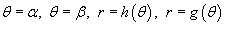 (рисунок 3). Тогда площадь этой области определяется формулой (рисунок 3). Тогда площадь этой области определяется формулой
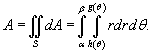
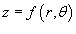 с основанием S, выражается в полярных координатах в виде с основанием S, выражается в полярных координатах в виде
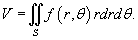 |
||||||||||||
|
Пример 1
|
||||||||||||
|
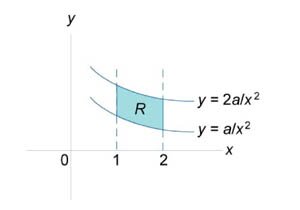
Найти площадь области R, ограниченной гиперболами
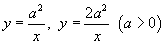 и вертикальными прямыми и вертикальными прямыми 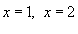 . .
Решение. 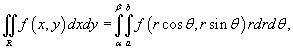 
|
||||||||||||
|
Пример 2
|
||||||||||||
|
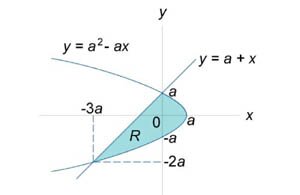
Вычислить площадь области R, ограниченной линиями
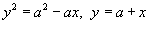 . .
Решение. 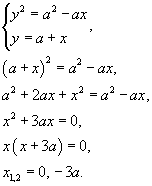 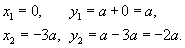 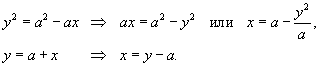 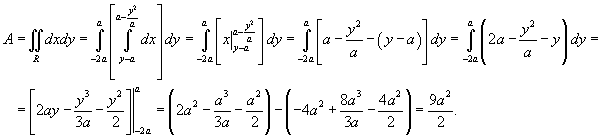 |
||||||||||||
|
Пример 3
|
||||||||||||
|
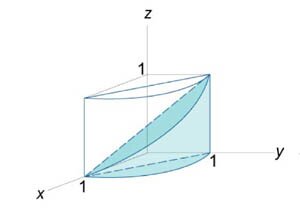
Найти объем тела в первом октанте, ограниченного плоскостями
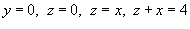 . .
Решение.
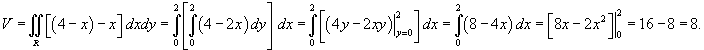 |
||||||||||||
|
Пример 4
|
||||||||||||
|
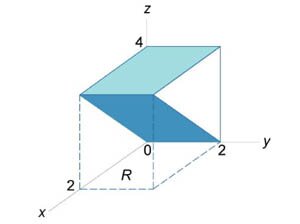
Описать тело, объем которого определяется интегралом
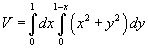 . .
Решение.
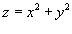 . Объем тела равен . Объем тела равен
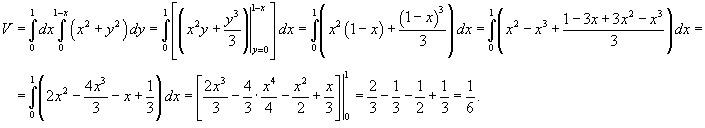 |
||||||||||||
|
Пример 5
|
||||||||||||
|
Вычислить объем тела, ограниченного поверхностями
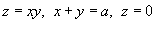 . .
Решение.
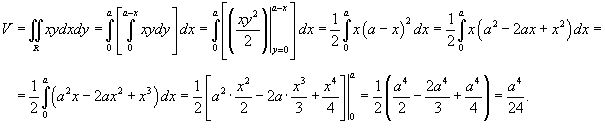 |
||||||||||||
|
Пример 6
|
||||||||||||
|
Найти объем тела, ограниченного поверхностями
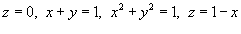 . .
Решение.
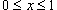 значения y изменяются от значения y изменяются от 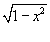 . Сверху тело ограничено плоскостью . Сверху тело ограничено плоскостью 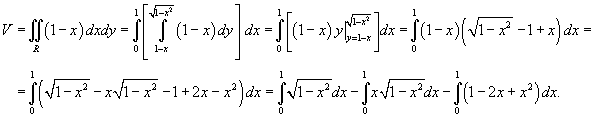 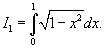 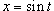 . Тогда . Тогда 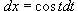 . Видно, что . Видно, что 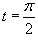 при при 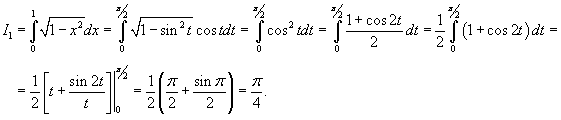 Вычислим второй интеграл 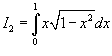 , используя замену переменной. Полагаем , используя замену переменной. Полагаем 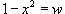 . Тогда . Тогда 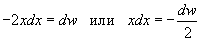 . Находим, что . Находим, что 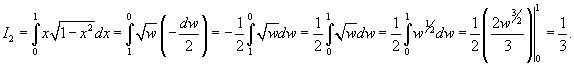 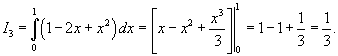 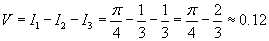 |
||||||||||||
|
Пример 7
|
||||||||||||
|
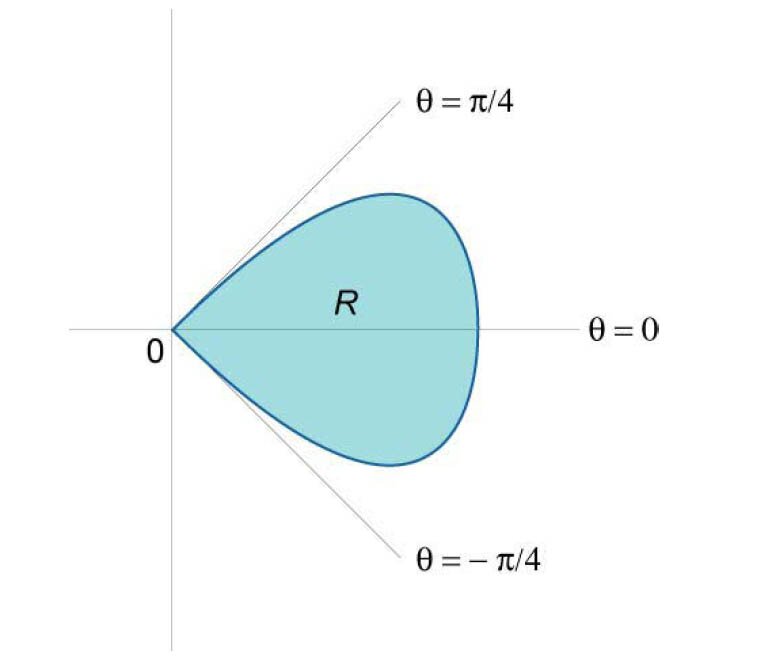
Найти площадь лепестка розы, заданной уравнением
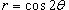 . .
Решение. 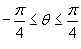 (рисунок 13). Область интегрирования имеет вид (рисунок 13). Область интегрирования имеет вид 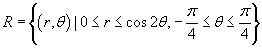 . Следовательно, площадь данной фигуры в полярных координатах равна . Следовательно, площадь данной фигуры в полярных координатах равна

|
||||||||||||
|
Пример 8
|
||||||||||||
|
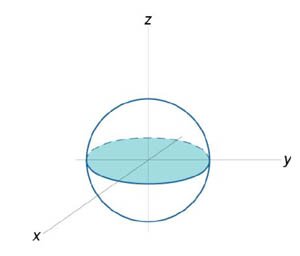
Вычислить объем единичного шара.
Решение. 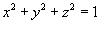 (рисунок 14). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на 2. Уравнение верхней полусферы записывается как (рисунок 14). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на 2. Уравнение верхней полусферы записывается как
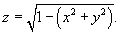 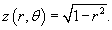 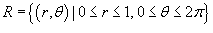 . Следовательно, объем верхнего полушара выражается формулой . Следовательно, объем верхнего полушара выражается формулой
 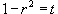 . Тогда . Тогда 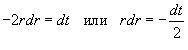 . Уточним пределы интегрирования: . Уточним пределы интегрирования: 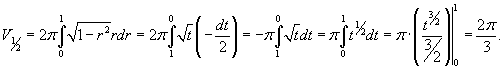 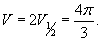 |
||||||||||||
|
Пример 9
|
||||||||||||
|
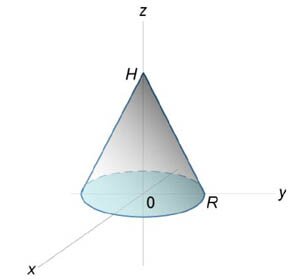
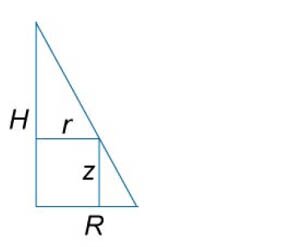
Используя полярные координаты, найти объем конуса высотой H и радиусом основания R (рисунок 15).
Решение.
 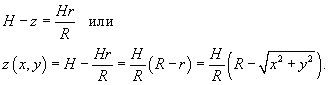  |
||||||||||||
|
Пример 10
|
||||||||||||
|
Вычислить площадь cферы радиуса a.
Решение.  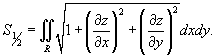 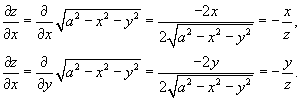 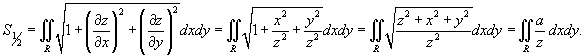 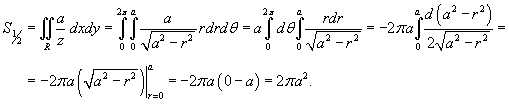 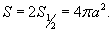 |
||||||||||||