|
Разложение в ряд Фурье непериодических функций
|
||||||
|
Разложение в ряд Фурье в интервале [−L, L]
Рассмотрим кусочно-непрерывную 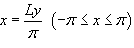 , преобразуем ее в функцию , преобразуем ее в функцию
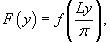 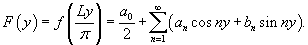 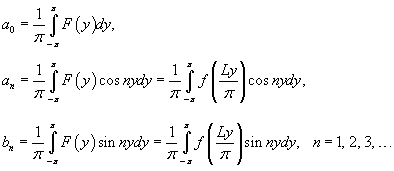 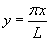 , получим следующие выражения для ряда Фурье исходной функции , получим следующие выражения для ряда Фурье исходной функции 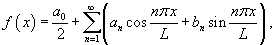 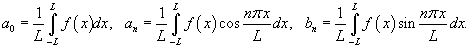
Разложение в ряд Фурье в интервале [a,b]
Если функция 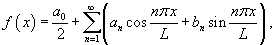 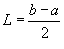 , а коэффициенты вычисляются следующим образом: , а коэффициенты вычисляются следующим образом:
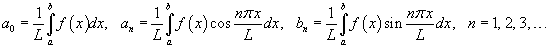
Четные и нечетные функции
Разложение в ряд Фурье четной функции, определенной в интервале 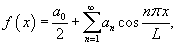 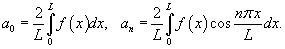 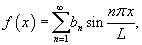 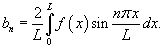 |
||||||
|
Пример 1
|
||||||
|
Найти разложение в ряд Фурье функции
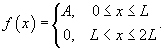 Решение. 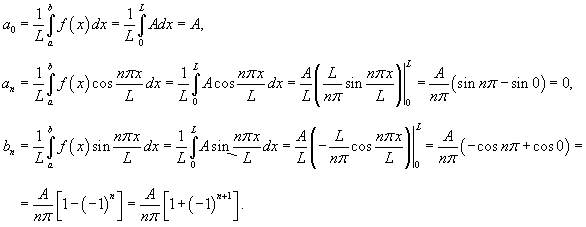  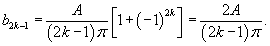 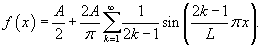
|
||||||
|
Пример 2
|
||||||
|
Найти разложение в ряд Фурье функции:
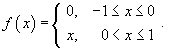 Решение. 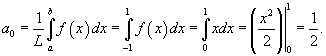 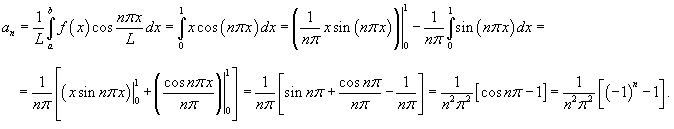 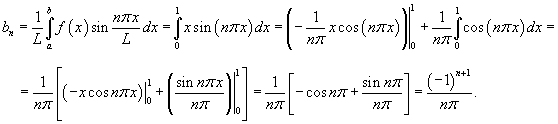 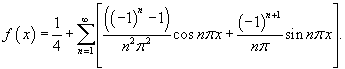 |
||||||
|
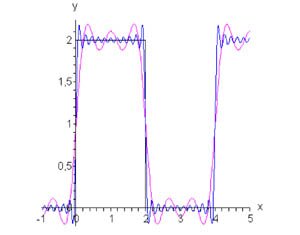
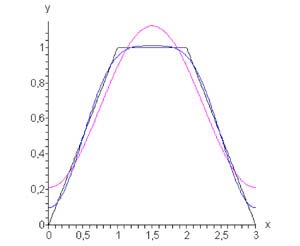
Пример 3
|
||||||
|
Найти разложение в ряд Фурье трапециевидной волны, заданной функцией
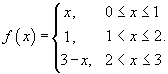 Решение. 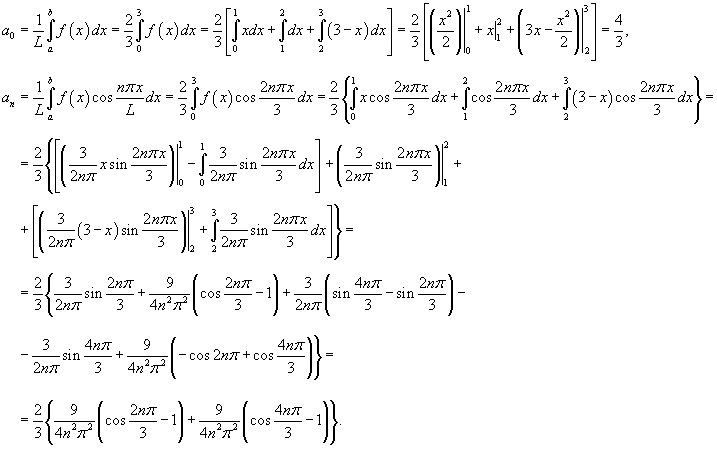 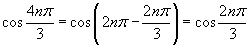 , то получаем , то получаем
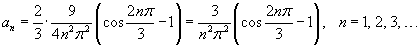 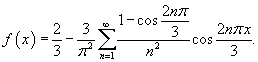
|
||||||
|
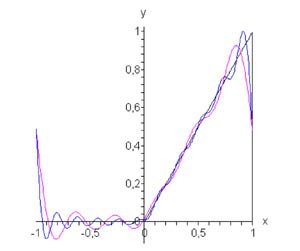
Пример 4
|
||||||
|
Найти разложение в ряд Фурье функции
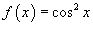 . .
Решение. 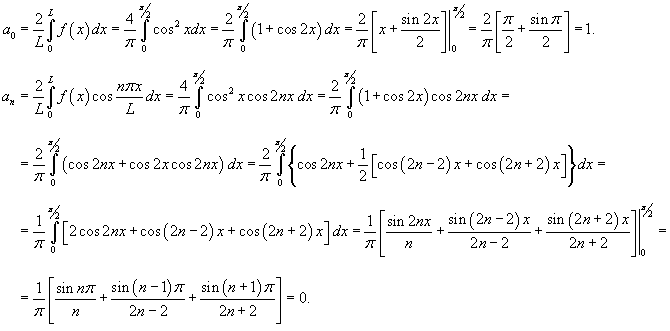 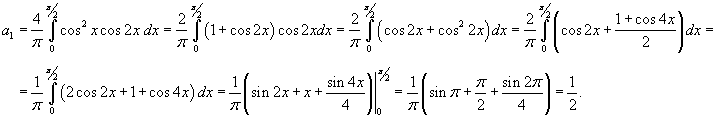 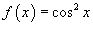 имеет вид имеет вид
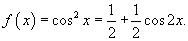 |
||||||