Вытекание жидкости из сосуда

Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей, в 1643 году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок 1) описывается формулой: где h − высота уровня жидкости над отверстием, g − гравитационная постоянная. Такая же формула описывает скорость тела, свободного падающего с высоты h в поле тяжести Земли в вакууме.

В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому, формула Торричелли часто записывается с дополнительным множителем φ: 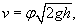где коэффициент φ близок к 1. Значения параметра φ для отверстий различной формы и размера можно найти в гидравлических справочниках. Вытекание жидкости из тонкой длинной трубки (рисунок 2) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.

Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть 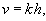где k − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.

Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого). Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус которого равен R. Предположим, что жидкость вытекает через малое отверстие радиуса a на дне сосуда (рисунок 3). Скорость жидкости описывается формулой Торричелли: где z − высота жидкости над отверстием. Тогда поток жидкости определяется выражением: Здесь πa² соответствует площади отверстия, через которое вытекает жидкость, а знак "минус" означает, что уровень жидкости уменьшается по мере ее вытекания из резервуара.

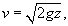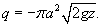Уравнение баланса жидкости в резервуаре описывается следующим образом: 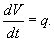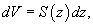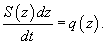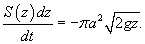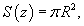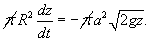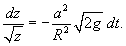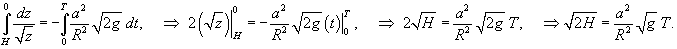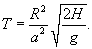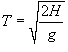Поскольку изменение объема dV можно выразить как то мы получаем дифференциальное уравнение Подставим функцию q(z) в это уравнение: Поперечное сечение S(z) цилиндрического сосуда не зависит от высоты z и равно где R − радиус основания цилиндра. Тогда В результате получаем уравнение с разделяющимися переменными: Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет H, и за время T он уменьшается до 0: Отсюда следует выражение для полного времени вытекания жидкости T: Интересно, что в предельном случае a = R (когда площади отверстия и самого цилиндра равны), полученная формула преобразуется в известную формулу , которая определяет время падения материального тела с высоты H. Зависимость времени T от высоты H схематически показана на рисунке 4.

Аналогично можно описать вытекание жидкости и из сосуда другой формы.

   Пример 1

Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания T. Радиус верхнего основания конического сосуда равен R, а радиус нижнего основания a. Начальная уровень жидкости составляет H (рисунок 5). Изменение уровня жидкости на высоте z описывается дифференциальным уравнением где S(z) − площадь поперечного сечения сосуда на высоте z, а q(z) − поток жидкости, зависящий от высоты z.

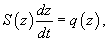Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать: 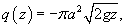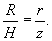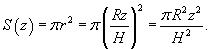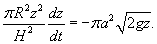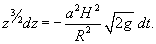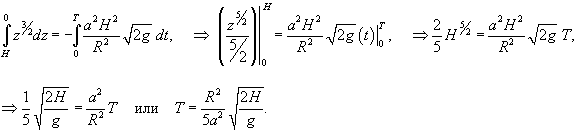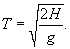где a − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник (рисунок 6 выше). Из подобия треугольников следует, что Следовательно, площадь поверхности жидкости на высоте z будет равна Подставляя S(z) и q(z) в дифференциальное уравнение, имеем: После простых преобразований получаем следующее дифференциальное уравнение: Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения H до нуля за время T: Здесь мы снова видим аналогию с падением материального тела с высоты H в гравитационном поле Земли. Как известно, время падения описывается формулой: Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых значениях H, R и a время вытекания жидкости из конического сосуда ровно в 5 раз меньше, чем из цилиндра (хотя объем конического сосуда меньше лишь в 3 раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?

   Пример 2

Исследовать вытекание жидкости из тонкой трубки радиусом R и высотой H, считая трубку полностью заполненной жидкостью. Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте z в следующей форме: В данном случае площадь поперечного сечения S(z) является константой и поток жидкости, вытекающей из сосуда, определяется формулой: где k зависит от размера отверстия, смачиваемости и других параметров.

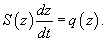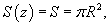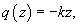В результате получаем простое дифференциальное уравнение: 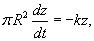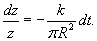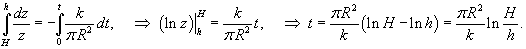или после разделения переменных: Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты H до h за время от 0 до t: Зависимость времени t от отношения H/h показана схематически на рисунке 8. Данная кривая аналогична зависимости времени T от высоты H для широкого цилиндрического сосуда, для которого справедлив закон Торричелли. Интересно, что в данной простой модели время вытекания жидкости t формально стремится к бесконечности при h → 0.