|
Первые интегралы
|
|
Определение производной Ли и первого интеграла системы
Рассмотрим систему n-го порядка
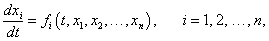 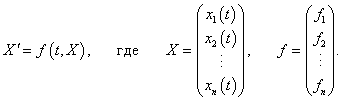 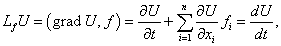 Введенная производная по направлению векторного поля (производная Ли) является обобщением понятия производной по постоянному направлению, которая широко используется при исследовании функций нескольких переменных. Если непостоянная функция 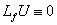 В случае автономных систем (когда правые части уравнений fi не зависят явно от переменной t), первый интеграл определяется более простым выражением: 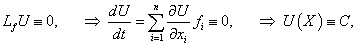 Как видно, первый интеграл остается постоянным вдоль любого решения X(t). Другими словами, фазовые траектории X(t) системы лежат на одной из поверхностей уровня первого интеграла U(X). В случае системы второго порядка это будут линии уровня первого интеграла. Предположим, что для автономной системы порядка n найдено k первых интегралов: 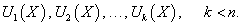 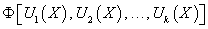 Первые интегралы 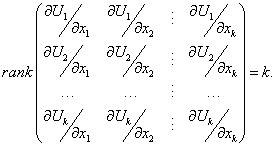
Метод интегрируемых комбинаций
Для того, чтобы найти первые интегралы, уравнения системы с помощью подходящих арифметических операций преобразуются к виду
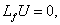
Симметричная форма системы дифференциальных уравнений
Для нахождения первых интегралов иногда удобно записать исходную систему в т.н. симметричной форме:
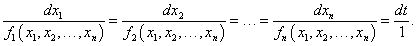 В такой записи некоторые пары отношений могут допускать интегрирование, например, методом разделения переменных. Другой способ решения системы в симметричной форме заключается в использовании свойства равных дробей 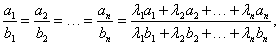 |
|
Пример 1
|
|
Решить систему уравнений
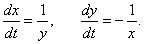
Решение.
Запишем систему в виде
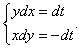 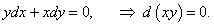 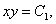 Выразим решения x(t), y(t) в явном виде. В первое уравнение подставим выражение 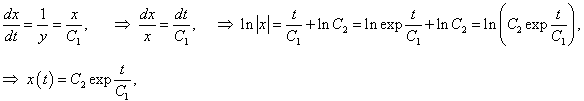 Теперь найдем выражение для y(t): 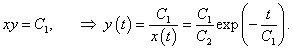 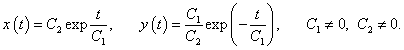 |
|
Пример 2
|
|
Решить систему уравнений
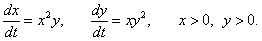
Решение.
Запишем систему в симметричной форме:
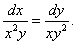 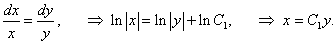 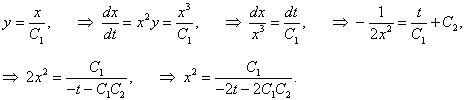 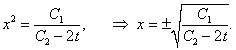 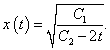 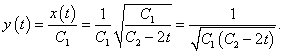 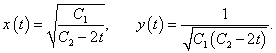 |
|
Пример 3
|
|
Найти общее решение системы дифференциальных уравнений
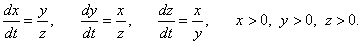
Решение.
Преобразуем уравнения системы, чтобы получить интегрируемые комбинации. Разделим второе уравнение на первое:
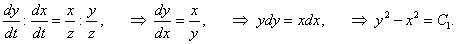 Аналогично, разделив третье уравнение на второе, найдем еще один первый интеграл: 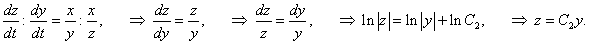 Найдем теперь решения x(t), y(t), z(t) в явном виде. Подставим выражения для x и z, соответственно, из первого и второго интеграла, в первое уравнение системы:  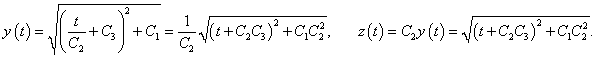 |
|
Пример 4
|
|
Найти общее решение системы с помощью первых интегралов
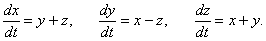
Решение.
Запишем систему уравнений в симметричной форме:
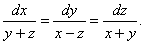 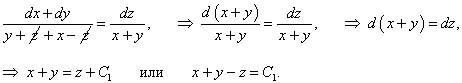 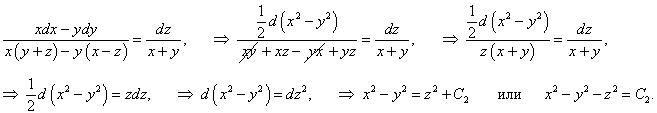 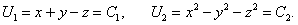 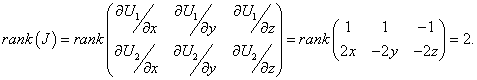 |