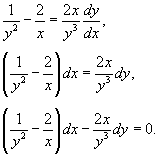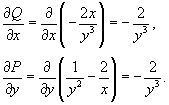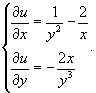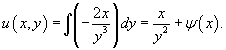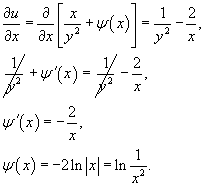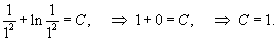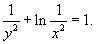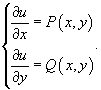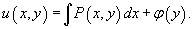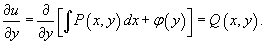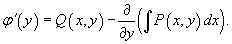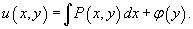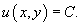|
|
|
|
Уравнения в полных дифференциалах
|
|
Определение уравнения в полных дифференциалах
Дифференциальное уравнение вида
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
Общее решение уравнения в полных дифференциалах определяется формулой
где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
Алгоритм решения уравнения в полных дифференциалах
- Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
- Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
- Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
- Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
Отсюда получаем выражение для производной неизвестной функции φ(y):
- Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
- Общее решение уравнения в полных дифференциалах записывается в виде:
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ(x).
|
|
Пример 1
|
|
Решить дифференциальное уравнение 2xydx + (x2 + 3y2)dy = 0.
Решение.
Данное уравнение является уравнением в полных дифференциалах, поскольку соответствующие частные производные равны:
Запишем следующую систему дифференциальных уравнений для определения функции u(x,y):
Интегрируя первое уравнение по x, получаем:
Подставляем выражение для u(x,y) во второе уравнение:
Интегрируя последнее уравнение, находим неизвестную функцию φ(y):
так что общее решение данного уравнения в полных дифференциалах имеет вид:
где C − произвольная постоянная.
|
|
Пример 2
|
|
Найти решение дифференциального уравнения (6x2 − y +3)dx + (3y2 − x − 2)dy = 0.
Решение.
Проверим, является ли данное уравнение уравнением в полных дифференциалах:
Как видно, мы имеем уравнение в полных дифференциалах. Запишем систему уравнений для определения функции u(x,y):
проинтегрируем первое уравнение по переменной x, полагая, что y является константой. В результате получаем:
Здесь мы ввели непрерывную дифференцируемую функцию φ(y) вместо постоянной C.
Подставим функцию u(x,y) во второе уравнение:
Получаем уравнение для производной φ'(y):
Интегрируя, находим функцию φ(y):
Таким образом, функция u(x,y) определяется формулой
Следовательно, общее решение уравнения описывается следующим неявным выражением:
где C − произвольное действительное число.
|
|
Пример 3
|
|
Решить дифференциальное уравнение e ydx + (2y + xe y)dy = 0.
Решение.
Сначала проверим, что данное уравнение будет являться уравнением в полных дифференциалах:
Видно, что 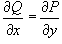 . Найдем далее функцию u(x,y) из системы уравнений:
Следовательно,
Теперь продифференцируем это выражение по переменной y и приравняем к 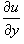 . В результате получим выражение для производной φ'(y):
Таким образом мы находим φ(y) и всю функцию u(x,y):
Следовательно, общее решение дифференциального уравнения записывается в виде:
|
|
Пример 4
|
|
Решить уравнение (2xy − sin x)dx + (x2 - cos y)dy = 0.
Решение.
Данное уравнение является уравнением в полных дифференциалах, поскольку
Найдем функцию u(x,y) из системы двух уравнений:
Интегрируя первое уравнение по переменной x, получаем:
Подставляя во второе уравнение, имеем:
Следовательно,
Тогда функция u(x,y) определятся выражением
а общее решение дифференциального уравнения описывается неявной формулой
|
|
Пример 5
|
|
Решить уравнение 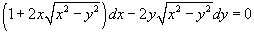
Решение.
Сначала выясним, имеем ли мы дело с уравнением в полных дифференциалах:
Как видно, 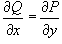 . Следовательно, это уравнение в полных дифференциалах. Найдем функцию u(x,y), удовлетворяющую системе уравнений:
Интегрируем первое уравнение:
где φ(y) − некоторая неизвестная функция, зависящая от y. Мы определим ее позже.
Подставим результат во второе уравнение системы:
Интегрируя последнее выражение, находим функцию φ(y):
где C − константа.
Таким образом, общее решение данного дифференциального уравнения описывается уравнением:
|
|
Пример 6
|
|
Решить дифференциальное уравнение 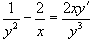 с начальным условием y(1) = 1.
Решение.
Проверим, что уравнение является уравнением в полных дифференциалах, предварительно преобразовав его в стандартную форму:
Частные производные будут равны
Следовательно, мы имеем дело с уравнением в полных дифференциалах. Поэтому, далее запишем следующую систему уравнений для определения функции u(x,y):
В данном случае удобнее проинтегрировать второе уравнение по переменной y:
Теперь продифференцируем это выражение по переменной x:
Итак, общее решение дифференциального уравнения в неявном виде определятся выражением:
Найдем теперь частное решение, удовлетворяющее начальному условию y(1) = 1. Подставляя начальные значения, определяем постоянную C:
Следовательно, частное решение данной задачи Коши имеет вид:
|
|
|
|
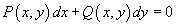
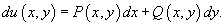
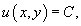
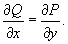
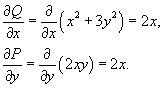
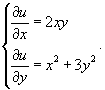
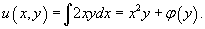
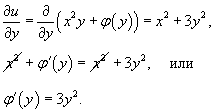
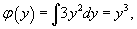
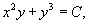
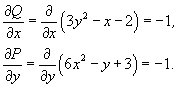
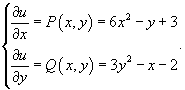
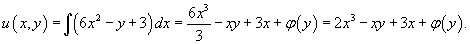
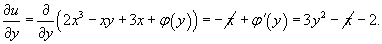
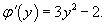
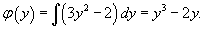

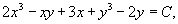
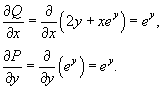
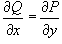 . Найдем далее функцию
. Найдем далее функцию 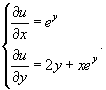
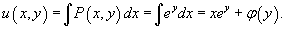
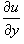 . В результате получим выражение для производной
. В результате получим выражение для производной 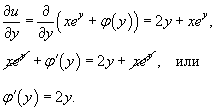
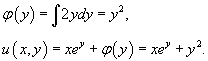
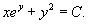
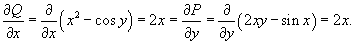
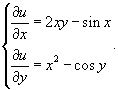
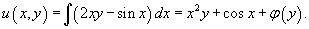
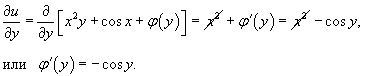
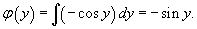
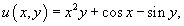
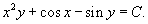
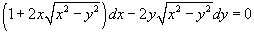
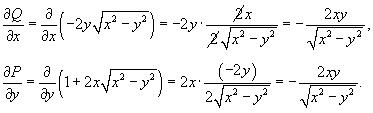
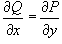 . Следовательно, это уравнение в полных дифференциалах. Найдем функцию
. Следовательно, это уравнение в полных дифференциалах. Найдем функцию 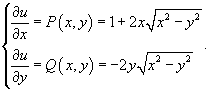
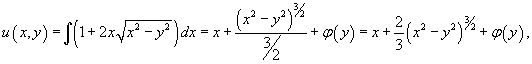
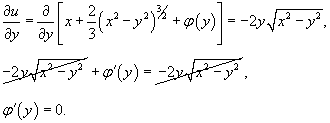
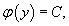
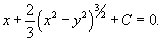
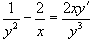 с начальным условием
с начальным условием