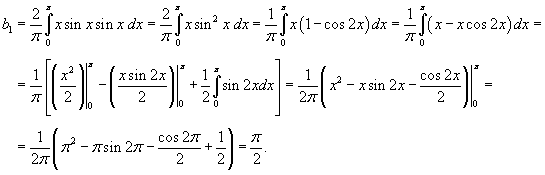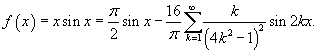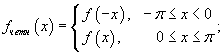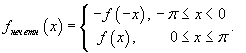|
|
|
|
Четные и нечетные продолжения
|
|
Предположим, что f (x) является кусочно-непрерывной функцией, заданной в интервале [0, π]. Чтобы найти разложение данной функции в ряд Фурье, нужно продолжить ее и построить в интервале [−π, π]. Это можно сделать двумя способами:
- можно построить четное продолжение f (x):
- или построить нечетное продолжение f (x):
В случае четной функции разложение в ряд Фурье описывается выражением
где
В случае нечетной функции, соответственно, получаем
где коэффициенты разложения равны
Понятие четного и нечетного продолжения функции можно ввести и для непериодической функции. Пусть функция f (x) определена в интервале [0, L]. Используя четное продолжение данной функции на интервал [− L, L], получим следующую формулу разложения в ряд Фурье:
где
В случае нечетного продолжения соответствующая формула имеет вид
где коэффициенты bn равны
|
|
Пример 1
|
|
Разложить по четным гармоникам функцию
Решение.
Разложить функцию по четным гармоникам − это значит построить четное продолжение заданной функции. Соответствующий ряд Фурье будет иметь вид
Вычислим коэффициенты a0 и an:
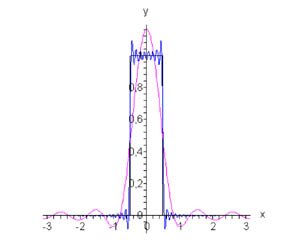
Таким образом, разложение ступенчатой функции в ряд Фурье по четным гармоникам определяется выражением
График данной функции и Фурье аппроксимации для случаев n = 5 и n = 50 приводятся на рисунке 1.
|
|
|
|
|
Рис.1, d = 0.5, n = 5, n = 50
|
|
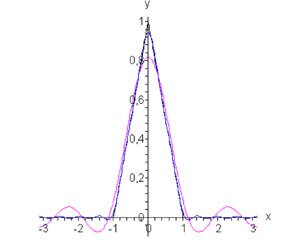
Рис.2, d = 1, n = 3, n = 10
|
|
|
Пример 2
|
|
Построить разложение в ряд Фурье по четным гармоникам для функции
Решение.
Используя четное продолжение первоначально заданной функции, можно записать
Коэффициенты Фурье a0 и an имеют значения:
Следовательно, Фурье разложение по четным гармоникам имеет вид (рисунок 2):
|
|
Пример 3
|
|
Построить нечетное продолжение функции 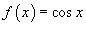 , заданной в интервале [0, π].
Решение.
Поскольку мы применяем нечетное продолжение, разложение в ряд Фурье будет иметь вид
Коэффициенты bn равны
Здесь мы учли, что
Найденное выражение для ов bn верно при n ≥ 2. Если n = 1, то получаем
Кроме того, можно заметить, что 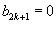 для нечетных n = 2k + 1. Для четных значений индекса n = 2k справедливо выражение
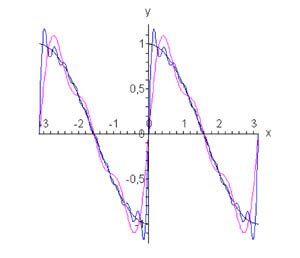
Таким образом, разложение в ряд Фурье по нечетным гармоникам имеет вид (рисунок 3):
|
|
|
|
|
Рис.3, n = 3, n = 10
|
|
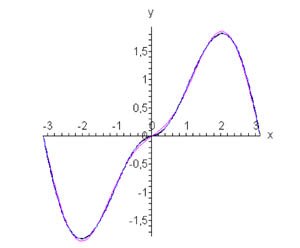
Рис.4, n = 1, n = 2
|
|
|
Пример 4
|
|
Построить нечетное продолжение функции 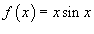 , заданной в интервале [0, π].
Решение.
Для нечетного продолжения ряд Фурье записывается в виде
Найдем коэффициенты bn:
Применяя интегрирование по частям, получаем
Поскольку
то выражение для коэффициентов bn упрощается:
Последняя формула верна при n ≥ 2. Заметим, что для четных n = 2k, 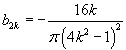 , а для нечетных n = 2k + 1, 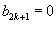 , где k = 1, 2, 3, ...
Вычислим отдельно b1:
Итак, разложение в ряд Фурье по нечетным гармоникам определяется формулой
На рисунке 4 (выше) показана исходная функция и ее Фурье аппроксимации при n = 1 и n = 2.
|
|
|
|
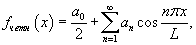
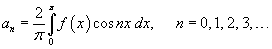
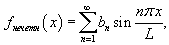
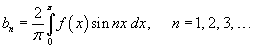
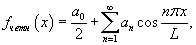
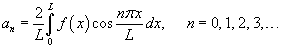
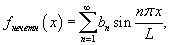
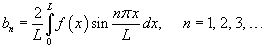
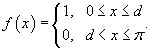
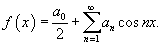
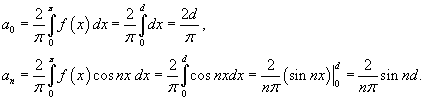
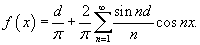

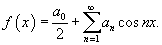
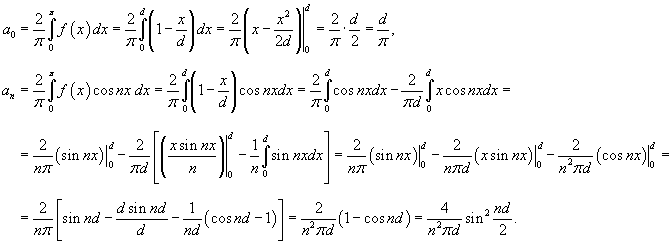
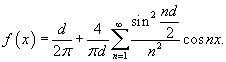
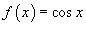 , заданной в интервале
, заданной в интервале 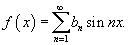
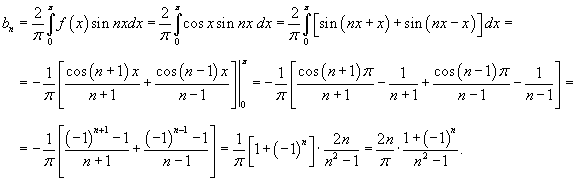
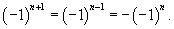
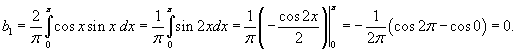
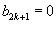 для нечетных
для нечетных 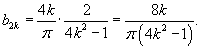
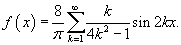
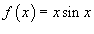 , заданной в интервале
, заданной в интервале 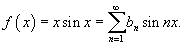
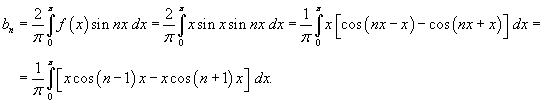
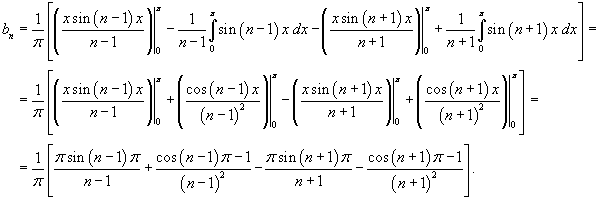
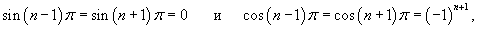
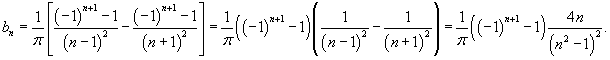
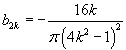 , а для нечетных
, а для нечетных 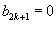 , где
, где