|
Уравнения, решаемые в квадратурах
|
||||||
|
Говорят, что дифференциальное уравнение решается в квадратурах, если его общее решение выражается через один или несколько интегралов.
Далее мы рассмотрим три типа уравнений высшего порядка, которые интегрируются в квадратурах.
Случай 1. Уравнение вида F(x, y (n)) = 0
Предположим сначала, что данное уравнение можно преобразовать в явную форму относительно производной y(n), т.е. выразить в виде
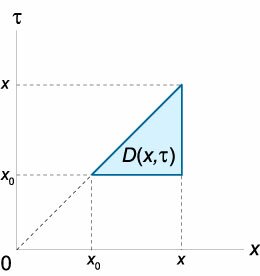
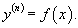 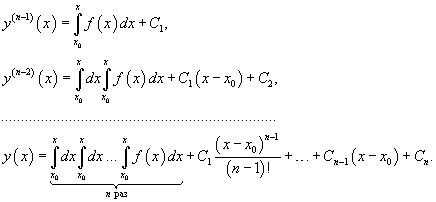 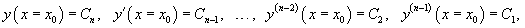 Повторный интеграл в выражении для 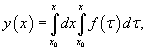 Данный повторный интеграл задан в треугольной области
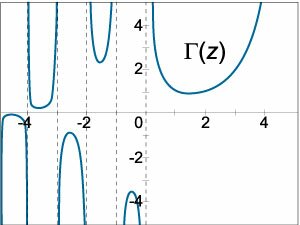
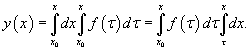 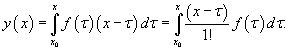 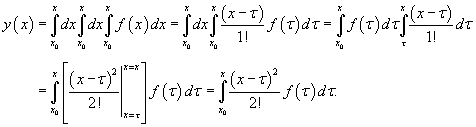 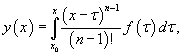 Полученное выражение представляет собой частное решение дифференциального уравнения 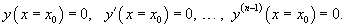 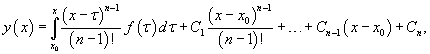 Вместо факториала 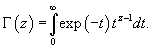 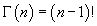 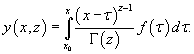 Данную формулу можно рассматривать как определение дробной производной порядка z, если исходная функция Мы рассмотрели решение явного дифференциального уравнения 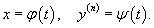 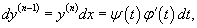 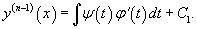 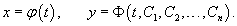
Случай 2. Уравнение вида F(y (n-1), y (n)) = 0
Рассмотрим сначала случай, когда такое уравнение можно разрешить относительно 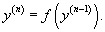 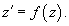 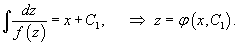 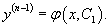 Общее неявное уравнение 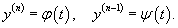 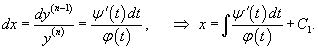 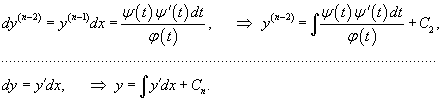
Случай 3. Уравнение вида F(y (n-2), y (n)) = 0
Предположим, что данное уравнение разрешено относительно 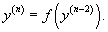 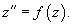 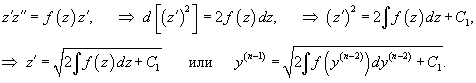 Если уравнение 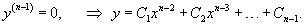 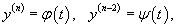 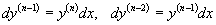 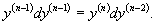 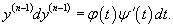 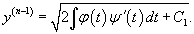 |
||||||
|
Пример 1
|
||||||
|
Найти общее решение дифференциального уравнения
Решение. 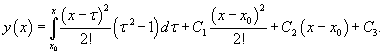 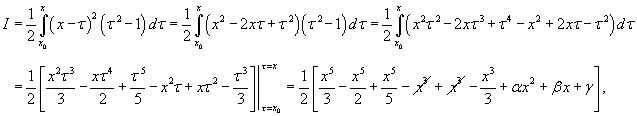 Тогда общее решение уравнения представляется в виде: 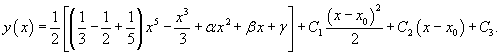 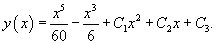 |
||||||
|
Пример 2
|
||||||
|
Найти частное решение уравнения
Решение. 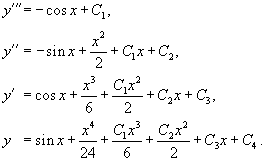 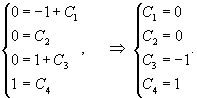 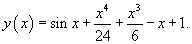 |
||||||
|
Пример 3
|
||||||
|
Найти общее решение уравнения
Решение. 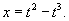 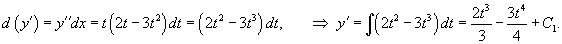 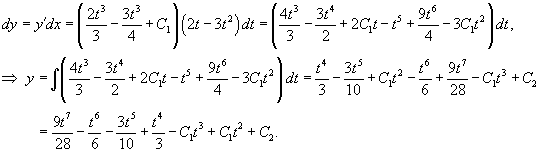 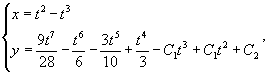 |
||||||
|
Пример 4
|
||||||
|
Найти частное решение уравнения
Решение. 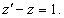 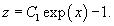 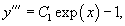 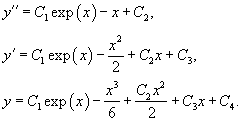 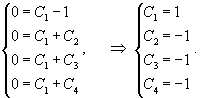 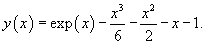 |
||||||
|
Пример 5
|
||||||
|
Найти общее решение дифференциального уравнения
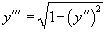 . .Решение. 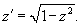 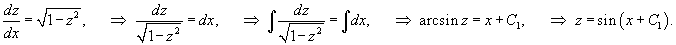 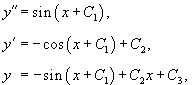 |
||||||
|
Пример 6
|
||||||
|
Построить общее решение уравнения
Решение.   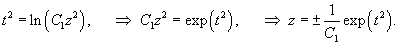 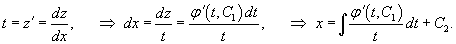 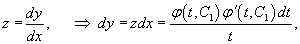 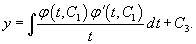 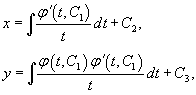 |
||||||