|
Уравнение цепной линии
|
||||||||||||
|
Цепной линией называется плоская кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной в обоих концах и провисающей под действием силы тяжести.
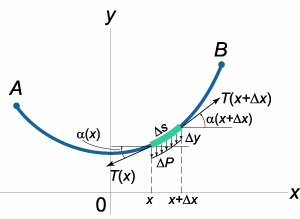
Цепная линия по форме напоминает параболу (рисунок 1). Так считалось долгое время. В начале 17 века Галилео Галилей высказал сомнение, что висящая цепь в действительности является параболой. Однако строгое доказательство и точный вывод были получены лишь полвека спустя − после того, как Исаак Ньютон и Готфрид Вильгельм Лейбниц разработали основы математического анализа. Решение задачи о цепной линии было опубликовано в 1691 году Христианом Гюйгенсом, Готфридом Вильгельмом Лейбницем и Иоганном Бернулли. Ниже мы рассмотрим вывод уравнения цепной линии и некоторые его вариации. Пусть тяжелая однородная нить подвешена в точках А, В, которые могут находиться на разной высоте (рисунок 2).
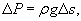 Условия равновесия выделенного элемента длиной 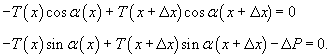 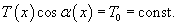 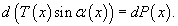 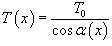 , то получаем , то получаем
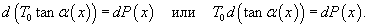 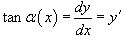 , так что уравнение равновесия записывается в дифференциальном виде как , так что уравнение равновесия записывается в дифференциальном виде как
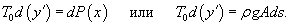 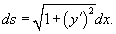 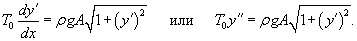 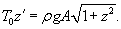 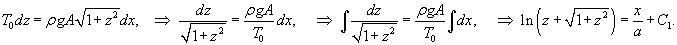 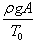 через 1/a. через 1/a.Касательная к цепной линии в нижней точке параллельна оси Ox. Следовательно, 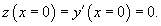 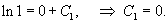 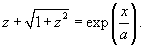 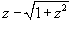 . Получаем: . Получаем:
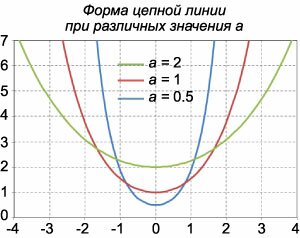
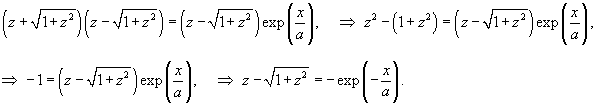 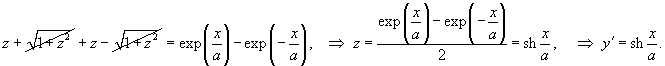 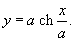 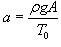 , зависимость от которого показана на рисунке 3. , зависимость от которого показана на рисунке 3.
В архитектуре и строительстве арки в форме перевернутой цепной линии (такие как арка Сааринена в Сент-Луисе, показанная на рисунке 4) обладают высокой устойчивостью благодаря тому, что внутренние силы сжатия идеально скомпенсированы и не вызывают прогиба. Цепная линия обладает еще одним интересным свойством. При вращении цепной линии вокруг оси Ox образуется поверхность, которая называется катеноидом. Катеноид представляет собой минимальную поверхность, т.е. любой ее участок будет по площади меньше, чем всякая другая поверхность, ограниченная тем же контуром. В частности, мыльная пленка между двумя окружностями, стремясь минимизировать свободную энергию, принимает форму катеноида. |
||||||||||||
|
Пример 1
|
||||||||||||
|
Определить форму каната подвесного моста.
Решение. 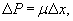 Тогда условие равновесия дифференциального элемента каната ds можно записать в виде 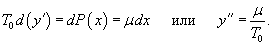 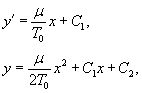 Таким образом, канат подвесного моста принимает форму не цепной линии, а параболы. Так выглядит, например, знаменитый мост "Золотые Ворота" в Сан-Франциско (рисунок 5).
|
||||||||||||
|
Пример 2
|
||||||||||||
|
Определить форму неоднородной цепной линии равного сопротивления.
Решение. В этом случае условия равновесия произвольного элемента нити (рисунок 1) записываются в виде  Из первого уравнения выразим T: 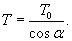 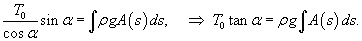 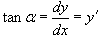 . Поэтому можно записать: . Поэтому можно записать:
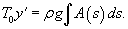 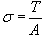 , то в правую часть уравнения подставим выражение , то в правую часть уравнения подставим выражение 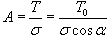 . Тогда наше уравнение принимает вид: . Тогда наше уравнение принимает вид:
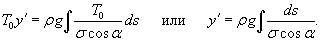 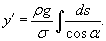 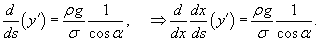 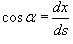 , то имеем следующее дифференциальное уравнение: , то имеем следующее дифференциальное уравнение:
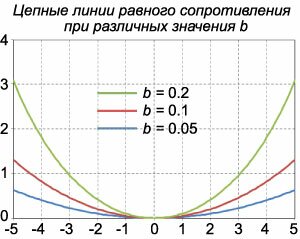
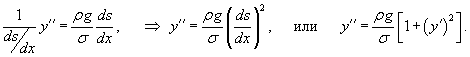 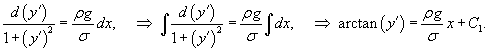 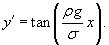 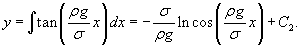 Итак, форма цепной линии равного сопротивления определяется функцией 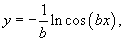 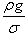 . График этой функции при различных значениях b представлен на рисунке 6. . График этой функции при различных значениях b представлен на рисунке 6.
|
||||||||||||