|
Двойные интегралы в прямоугольной области
|
|
Пусть область интегрирования R представляет собой прямоугольник
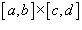 . Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде: . Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:
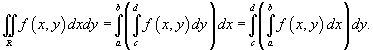 В частном случае, когда подынтегральная функция  |
|
Пример 1
|
|
Вычислить двойной интеграл
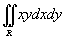 в области в области 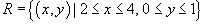 . .
Решение.  |
|
Пример 2
|
|
Вычислить двойной интеграл
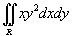 , заданный в области , заданный в области  . .
Решение. 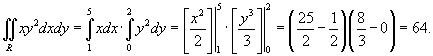 |
|
Пример 3
|
|
Вычислить интеграл
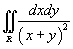 , заданный в области , заданный в области 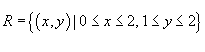 . .
Решение. 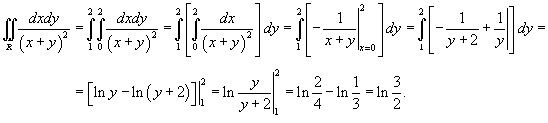 |
|
Пример 4
|
|
Вычислить интеграл
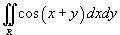 в области в области 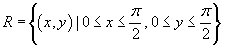 . .
Решение. 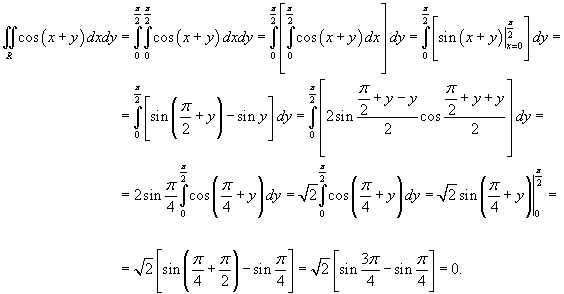 |
|
Пример 5
|
|
Вычислить интеграл
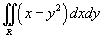 , заданный в области , заданный в области 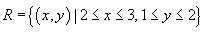 . .
Решение. 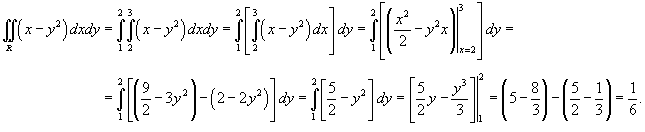 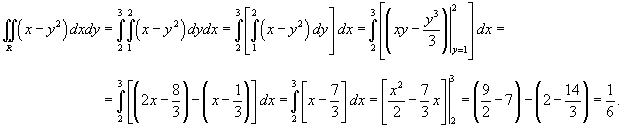 |