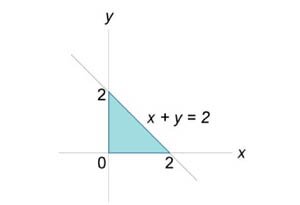|
Двойные интегралы в произвольной области
|
||||||
|
Пусть область интегрирования R типа I (элементарная относительно оси Oy) ограничена графиками функций
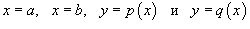 . При этом выполняются неравенства . При этом выполняются неравенства 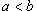 и и 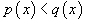 для всех для всех 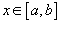 . Тогда двойной интеграл по области R выражается через повторный по формуле . Тогда двойной интеграл по области R выражается через повторный по формуле
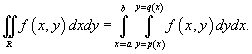 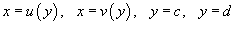 при условии, что при условии, что 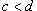 и и 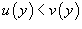 для всех для всех 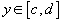 . Тогда двойной интеграл, заданный в области R, выражается через повторный интеграл по формуле . Тогда двойной интеграл, заданный в области R, выражается через повторный интеграл по формуле
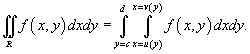 |
||||||
|
Пример 1
|
||||||
|
Вычислить интеграл
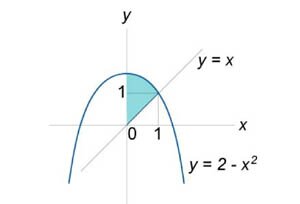
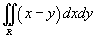 . Область интегрирования R ограничена графиками функций . Область интегрирования R ограничена графиками функций 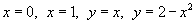 . .
Решение. 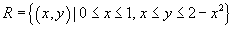 и относится к типу I (рисунок 1). Выразим двойной интеграл через повторный: и относится к типу I (рисунок 1). Выразим двойной интеграл через повторный:
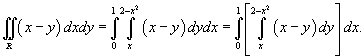 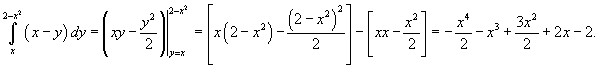 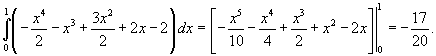
|
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
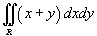 . Область интегрирования R ограничена прямыми . Область интегрирования R ограничена прямыми 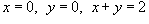 . .
Решение. 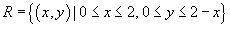 (рисунок 2) и является областью I типа (элементарной относительно оси Oy). Преобразуя двойной интеграл в повторный, получаем: (рисунок 2) и является областью I типа (элементарной относительно оси Oy). Преобразуя двойной интеграл в повторный, получаем:
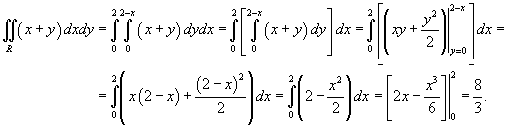 |
||||||
|
Пример 3
|
||||||
|
Вычислить интеграл
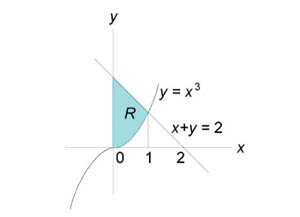
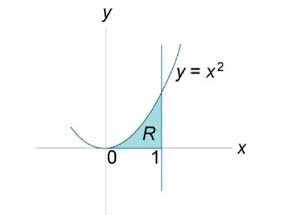
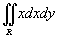 , в котором область интегрирования R ограничена графиками функций , в котором область интегрирования R ограничена графиками функций 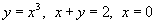 . .
Решение. 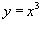 и линейная функция и линейная функция 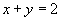 пересекаются в точке (1,1). Следовательно, двойной интеграл равен пересекаются в точке (1,1). Следовательно, двойной интеграл равен
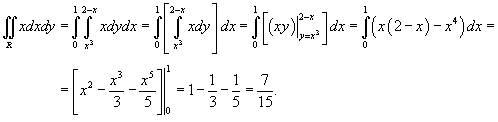
|
||||||
|
Пример 4
|
||||||
|
Найти интеграл
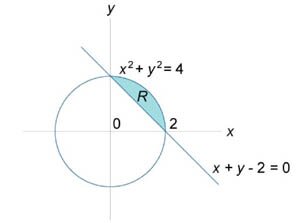
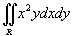 , где область R представляет собой сегмент окружности. Границы сегмента заданы уравнениями , где область R представляет собой сегмент окружности. Границы сегмента заданы уравнениями 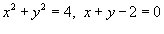 . .
Решение. 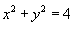 имеет радиус 2 и центр в начале координат. Область интегрирования показана на рисунке 4. Поскольку верхняя полуокружность описывается уравнением имеет радиус 2 и центр в начале координат. Область интегрирования показана на рисунке 4. Поскольку верхняя полуокружность описывается уравнением 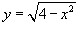 , то двойной интеграл вычисляется следующим образом: , то двойной интеграл вычисляется следующим образом:
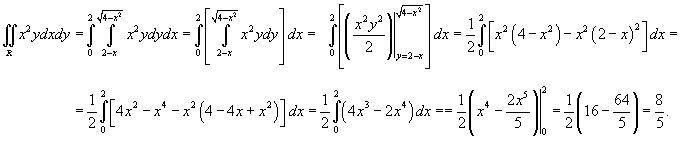 |
||||||
|
Пример 5
|
||||||
|
Найти интеграл
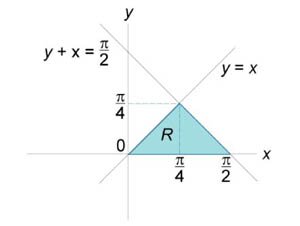
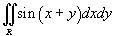 , заданный в области R, ограниченной прямыми , заданный в области R, ограниченной прямыми 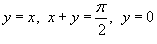 . .
Решение. 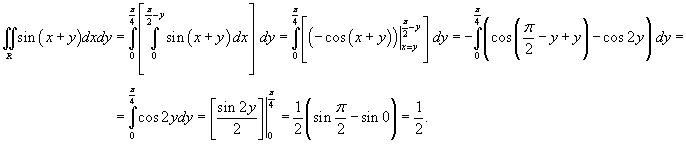
|
||||||
|
Пример 6
|
||||||
|
Найти интеграл
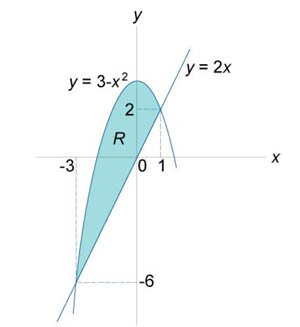
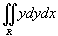 , где R ограничена прямой , где R ограничена прямой 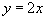 и параболой и параболой 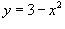 . .
Решение. 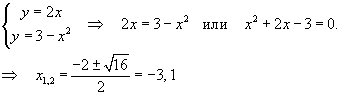 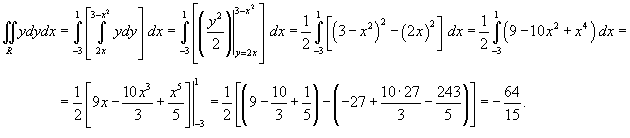 |
||||||
|
Пример 7
|
||||||
|
Найти интеграл
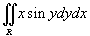 , где область R ограничена линиями , где область R ограничена линиями 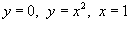 . .
Решение. 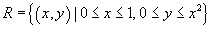 и показана ниже на рисунке 7. Двойной интеграл равен и показана ниже на рисунке 7. Двойной интеграл равен
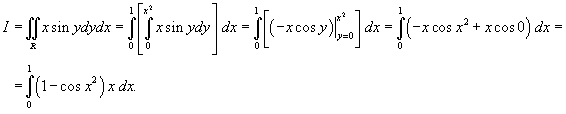 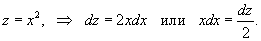 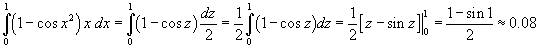
|
||||||
|
Пример 8
|
||||||
|
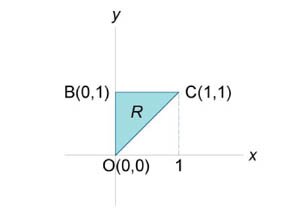
Вычислить интеграл
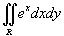 . Область интегрирования представляет собой треугольник с вершинами . Область интегрирования представляет собой треугольник с вершинами Решение. 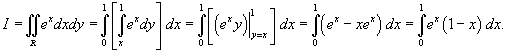 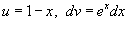 . Тогда . Тогда 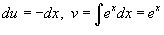 . Следовательно, . Следовательно,
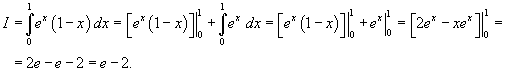 |
||||||
|
Пример 9
|
||||||
|
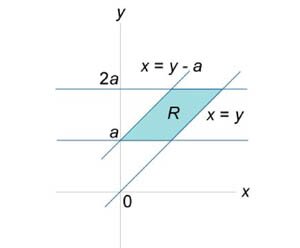
Вычислить интеграл
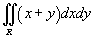 , где область R представляет собой параллелограмм со сторонами , где область R представляет собой параллелограмм со сторонами 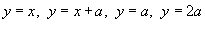 , a − некоторый параметр. , a − некоторый параметр.
Решение. 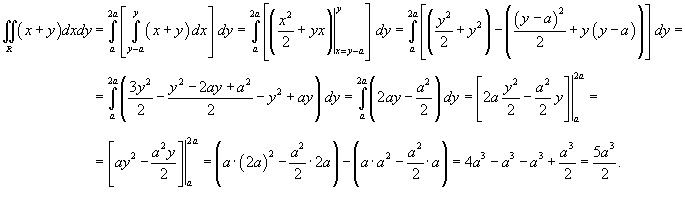
|
||||||