|
Дифференцирование и интегрирование степенных рядов
|
|
Рассмотрим степенной ряд
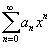 , имеющий радиус сходимости , имеющий радиус сходимости 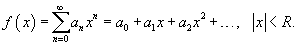 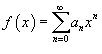 является непрерывной функцией при является непрерывной функцией при 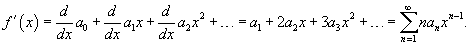 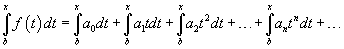 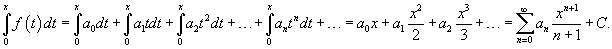 |
|
Пример 1
|
|
Показать, что
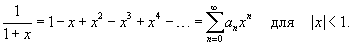
Решение.
Рассмотрим сначала следующий степенной ряд:
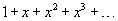 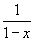 . Подставляя . Подставляя 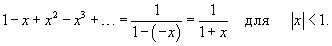 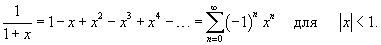 |
|
Пример 2
|
|
Найти разложение в степенной ряд для рациональной дроби
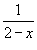 . .
Решение.
Запишем функцию в виде
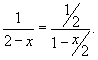 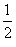 и знаменателем и знаменателем 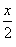 : :
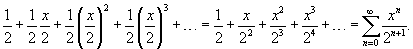 |
|
Пример 3
|
|
Найти разложение функции
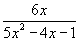 в степенной ряд. в степенной ряд.
Решение.
Сначала разложим данную функцию на сумму простейших рациональных дробей, используя метод неопределенных коэффициентов. Так как 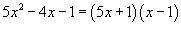 , то можно записать , то можно записать
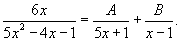 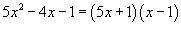 . Получаем . Получаем
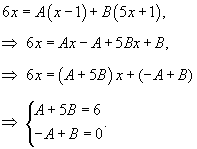 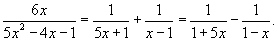 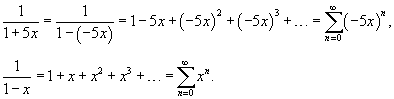 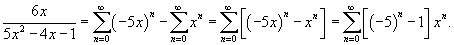 |
|
Пример 4
|
|
Найти представление в виде степенного ряда функции
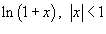 . .
Решение.
Выше в примере 1 мы получили разложение
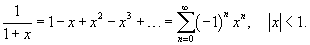 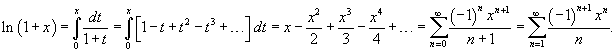 |
|
Пример 5
|
|
Разложить в степенной ряд интеграл
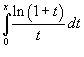 . .
Решение.
В предыдущем примере было найдено разложение логарифмической функции в ряд в виде
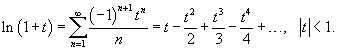 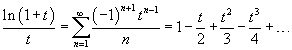 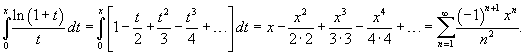 |
|
Пример 6
|
|
Разложить в степенной ряд экспоненциальную функцию
Решение. 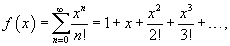 Дифференцируя его почленно, получаем 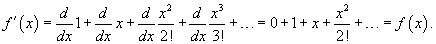 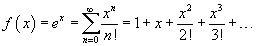 |
|
Пример 7
|
|
Разложить в степенной ряд гиперболический синус
Решение. 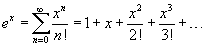 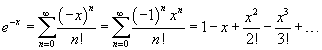 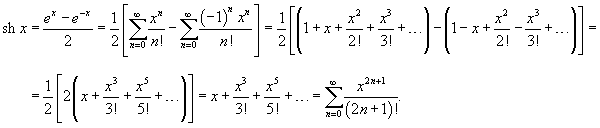 |