|
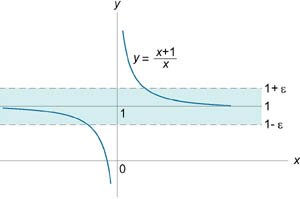
Определение предела функции
|
||||||
|
Определение предела по Коши и Гейне
Пусть функция Число L называется пределом функции 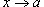 , если для каждого , если для каждого 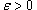 существует такое число существует такое число 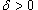 , что , что
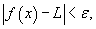 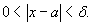 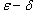 - определение или определение Коши. - определение или определение Коши.Существует также определение предела функции по Гейне, согласно которому функция  , сходящейся к точке a, последовательность , сходящейся к точке a, последовательность 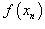 сходится к L. Определения предела функции по Коши и Гейне эквивалентны. сходится к L. Определения предела функции по Коши и Гейне эквивалентны.
Односторонние пределы
Символом 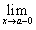 обозначается левосторонний предел, в котором переменная x, приближаясь к a, принимает значения обозначается левосторонний предел, в котором переменная x, приближаясь к a, принимает значения 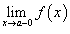 называется левосторонним пределом функции называется левосторонним пределом функции Аналогично, символом 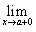 обозначается правосторонний предел, в котором переменная x, приближаясь к a, принимает значения обозначается правосторонний предел, в котором переменная x, приближаясь к a, принимает значения 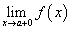 называется правосторонним пределом функции называется правосторонним пределом функции Отметим, что двусторонний предел 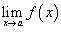 существуют лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть существуют лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть 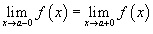 . В этом случае . В этом случае
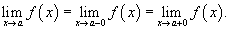 |
||||||
|
Пример 1
|
||||||
|
Используя
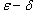 - определение предела, показать что - определение предела, показать что 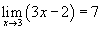 . .
Решение. 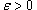 является произвольным положительным числом. Выберем является произвольным положительным числом. Выберем 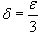 . Очевидно, что если . Очевидно, что если
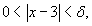 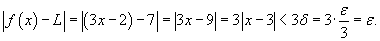 |
||||||
|
Пример 2
|
||||||
|
Используя
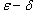 - определение предела, показать что - определение предела, показать что 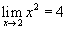 . .
Решение.  , т.е. , т.е.
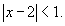 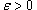 является произвольным положительным числом. Тогда можно записать следующее неравенство: является произвольным положительным числом. Тогда можно записать следующее неравенство:
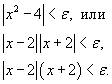 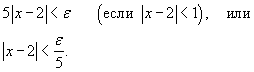 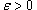 мы можем выбрать число δ такое, что мы можем выбрать число δ такое, что
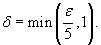 |
||||||
|
Пример 3
|
||||||
|
Используя
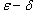 - определение предела, найти значение δ, соответствующее заданному числу ε для следующего предела - определение предела, найти значение δ, соответствующее заданному числу ε для следующего предела
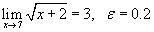 Решение.  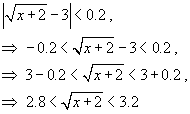 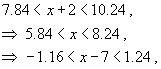 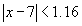 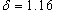 , чтобы исходное неравенство выполнялось. , чтобы исходное неравенство выполнялось. |
||||||
|
Пример 4
|
||||||
|
Доказать, что
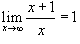 . .
Решение. 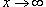 . Предположим, что . Предположим, что 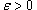 . Нам необходимо, чтобы выполнялось следующее неравенство: . Нам необходимо, чтобы выполнялось следующее неравенство:
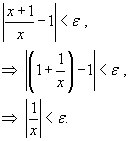 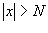 . Неравенство . Неравенство 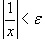 будет удовлетворено, если будет удовлетворено, если
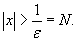 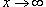 ) )
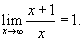
|
||||||
|
Пример 5
|
||||||
|
Доказать, что
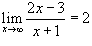 . .
Решение. 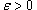 . Найдем число N - такое, что для любого . Найдем число N - такое, что для любого 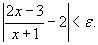 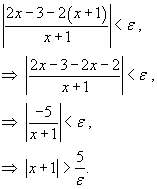 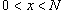 , то , то 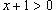 и можно просто записать и можно просто записать
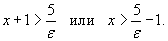 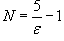 (или (или 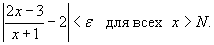 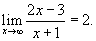 |
||||||