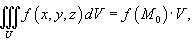|
|
|
|
Определение и свойства тройных интегралов
|
|
Определение тройного интеграла
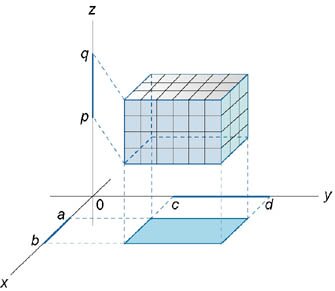
Формально определение тройного интеграла можно ввести аналогично двойному интегралу как предел суммы Римана. Начнем с простейшего случая, когда область интегрирования U имеет вид параллелепипеда 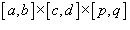 (рисунок 1).
Пусть множество чисел {x0, x1, ..., xm} разбивает отрезок [a, b] на малые интервалы, так что справедливо соотношение
Аналогично построим разбиение отрезка [c, d] вдоль оси O y и [p, q] вдоль оси O z:
Сумма Римана функции f (x,y,z) над разбиением 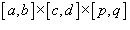 имеет вид
Здесь (ui , vj , wk) - некоторая точка в параллелепипеде (xi−1, xi)×(yi−1, yi)×(zi−1, zi), а приращения равны
Тройной интеграл от функции f (x,y,z) в параллелепипеде 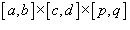 определяется как предел суммы Римана, при котором максимальное значение приращений Δxi, Δyj и Δzk стремятся к нулю:
Чтобы определить тройной интеграл в произвольной области U, выберем параллелепипед 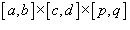 , включающий заданную область U. Введем функцию g (x,y,z), такую, что
Тогда тройной интеграл от функции функции f (x,y,z) в произвольной области U определяется в виде:
Основные свойства тройного интеграла
Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:
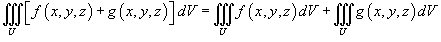
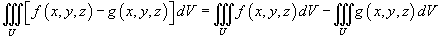
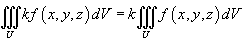 , где k - константа; , где k - константа;
- Если
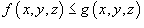 в любой точке области U, то в любой точке области U, то 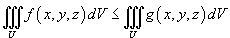 ; ;
- Если область U является объединением двух непересекающихся областей U1 и U2, то
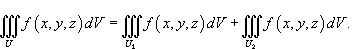 ; ;
- Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:
где V - объем области интегрирования U.
-
Теорема о среднем значении тройного интеграла.
Если функция f (x,y,z) непрерывна в области U, то существует точка M0 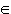 U, такая, что
где V - объем области U. U, такая, что
где V - объем области U.
|
|
Пример 1
|
|
Оценить максимальное значение тройного интеграла
где U представляет собой шар с центром в начале координат и радиусом R = 6.
Решение.
Уравнение шара имеет вид
Используя свойство 6, можно записать
где объем шара V равен
Максимальное значение M подынтегральной функции равно
Отсюда получаем верхнюю оценку тройного интеграла:
|
|
Пример 2
|
|
Оценить максимальное и минимальное значение тройного интеграла
где область U является параллелепипедом:
Решение.
Сначала вычислим объем области интегрирования U:
Оценка интеграла выглядит как
Здесь минимальное значение m подынтегральной функции равно
Соответственно, максимальное значение M составляет
Таким образом, оценка интеграла имеет вид
|
|
|
|
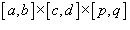 (рисунок 1).
(рисунок 1).
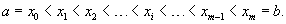
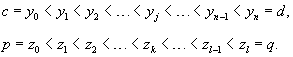
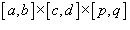 имеет вид
имеет вид
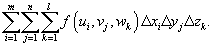
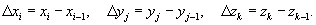
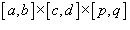 определяется как предел суммы Римана, при котором максимальное значение приращений
определяется как предел суммы Римана, при котором максимальное значение приращений 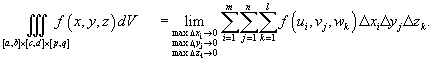
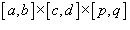 , включающий заданную область U. Введем функцию
, включающий заданную область U. Введем функцию 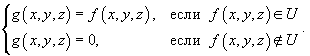
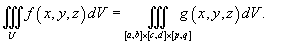
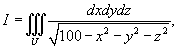
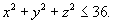
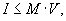
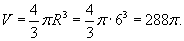
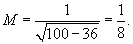
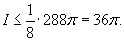
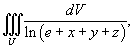
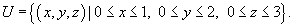
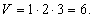
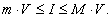
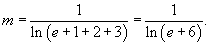
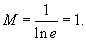
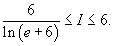
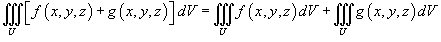
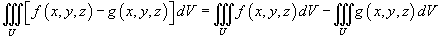
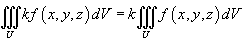 , где k - константа;
, где k - константа;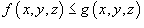 в любой точке области U, то
в любой точке области U, то 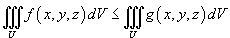 ;
;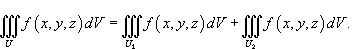 ;
;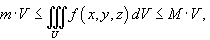
 U, такая, что
U, такая, что