|
Определение и свойства двойных интегралов
|
||||||||||||||||||
|
Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных   от функции одной переменной от функции одной переменной  выражает площадь под кривой выражает площадь под кривой
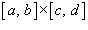 (рисунок 2). Используя ряд чисел (рисунок 2). Используя ряд чисел 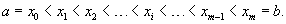 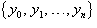 является разбиением отрезка является разбиением отрезка 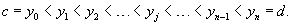 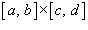 называется выражение называется выражение
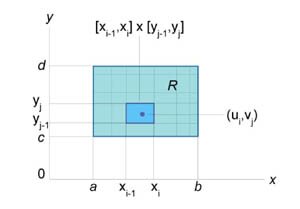
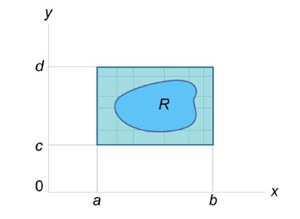
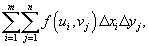 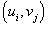 - некоторая точка в прямоугольнике - некоторая точка в прямоугольнике 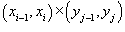 и и 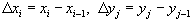 . .Двойной интеграл от функции 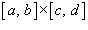 определяется как предел суммы Римана, при котором максимальные значения определяется как предел суммы Римана, при котором максимальные значения 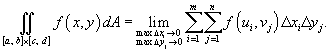 Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник 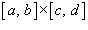 , покрывающий область R (рисунок 3), и введем функцию , покрывающий область R (рисунок 3), и введем функцию 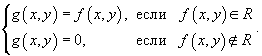 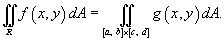
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:
|
||||||||||||||||||
|
Пример
|
||||||||||||||||||
|
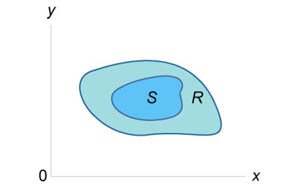
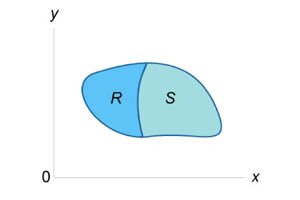
Пусть R и S являются непересекающимися областями (рисунок 5). Известны значения двойных интегралов:
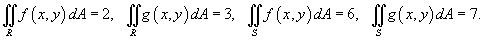 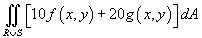 . .
Решение. 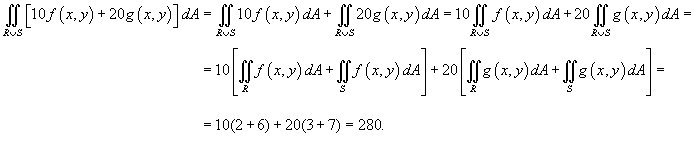 |
||||||||||||||||||



 , где k - константа;
, где k - константа; в области R, то
в области R, то  ;
; в области R и
в области R и  (рисунок 4), то
(рисунок 4), то  ;
; .
. означает объединение этих двух областей.
означает объединение этих двух областей.