|
Кривизна плоских кривых
|
||||||
|
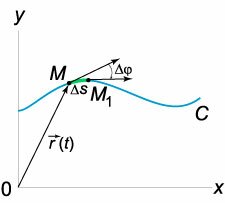
Пусть плоская кривая C задана параметрически радиус-вектором
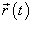 . При движении произвольной точки M вдоль кривой C ее касательная меняет направление (рисунок 1). . При движении произвольной точки M вдоль кривой C ее касательная меняет направление (рисунок 1).
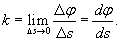 Если кривая задана своим радиусом вектором 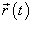 , ее кривизна определяется формулой , ее кривизна определяется формулой
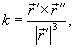 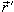 , , 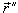 − первая и вторая производные радиус-вектора. В этой формуле в числителе записано векторное произведение векторов − первая и вторая производные радиус-вектора. В этой формуле в числителе записано векторное произведение векторов 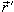 и и 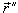 . .При параметрическом задании координат кривой 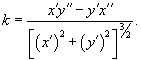 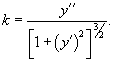 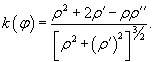 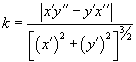 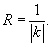 |
||||||
|
Пример 1
|
||||||
|
Определить радиус кривизны прямой.
Решение. Абсолютное значение кривизны вычисляется по формуле 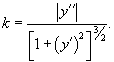 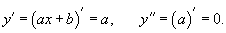 |
||||||
|
Пример 2
|
||||||
|
Определить уравнение переходной кривой железнодорожного пути.
Решение. 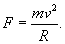 Пусть переходная кривая соответствует дуге OP (рисунок 3), длина которой равна L. При движении точки M вдоль этой кривой радиус кривизны изменяется пропорционально пройденному пути s: 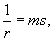 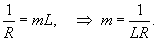 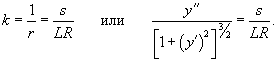 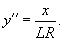 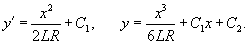 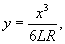 |
||||||
|
Пример 3
|
||||||
|
Найти кривую, у которой радиус кривизны является постоянной величиной.
Решение. 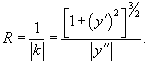 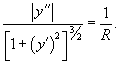 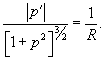 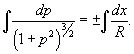 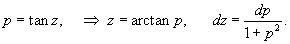 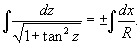 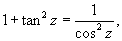 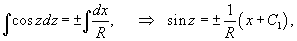 Перейдем обратно к переменной p, учитывая соотношение  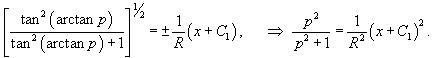 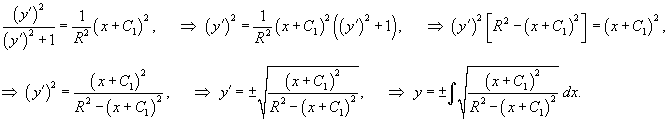 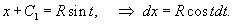 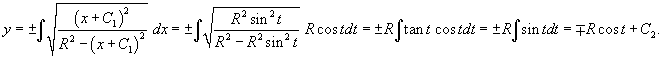 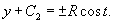 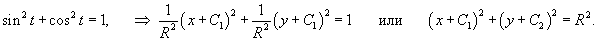 |
||||||