|
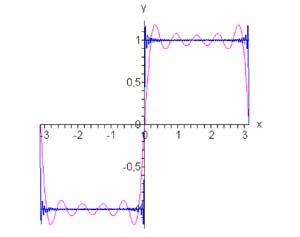
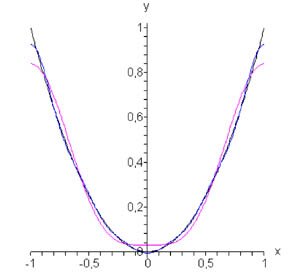
Комплексная форма рядов Фурье
|
||||||
|
Пусть функция
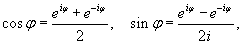 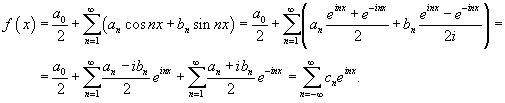 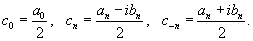 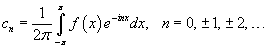 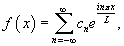 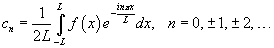 |
||||||
|
Пример 1
|
||||||
|
Используя комплексную форму записи, найти разложение в ряд Фурье функции
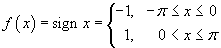 Решение. 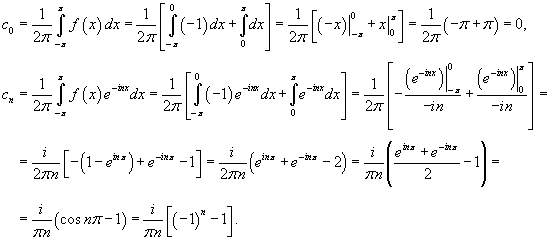 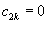 . .Если 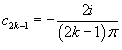 . .Следовательно, разложение в ряд Фурье в комплексной форме имеет вид: 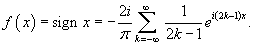 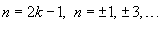 . Тогда . Тогда
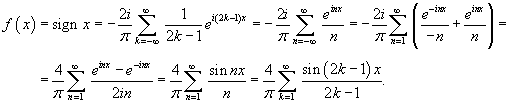
|
||||||
|
Пример 2
|
||||||
|
Найти разложение в ряд Фурье в комплексной форме для функции
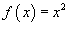 , заданной в интервале , заданной в интервале Решение. 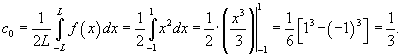 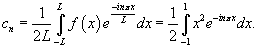 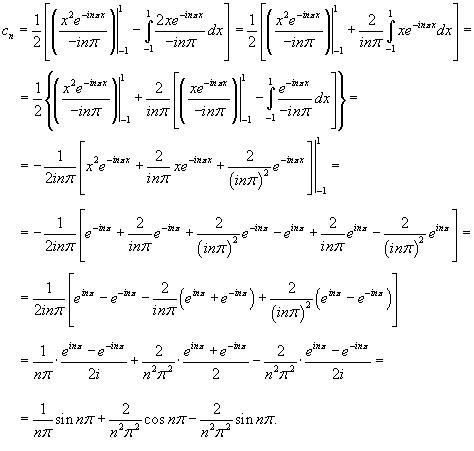 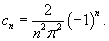 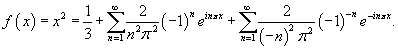 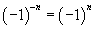 , можно окончательно записать , можно окончательно записать
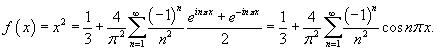 |
||||||
|
Пример 3
|
||||||
|
Используя комплексную форму записи, найти ряд Фурье для функции
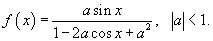 Решение. 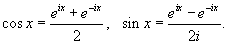 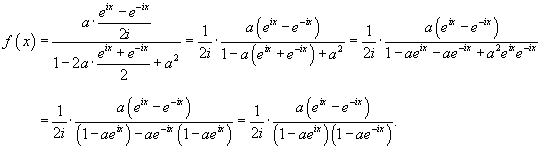 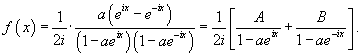 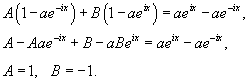 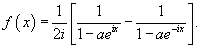 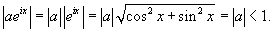 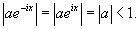 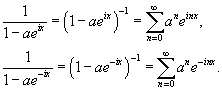 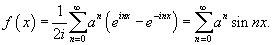 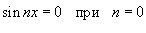 , то окончательный ответ будет , то окончательный ответ будет
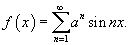 |
||||||