Дифференциальное уравнение Чебышева

Дифференциальное уравнение вида где |x| < 1, а n − действительное число, называется уравнением Чебышева в честь знаменитого российского математика Пафнутия Чебышева.

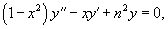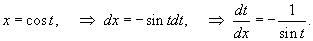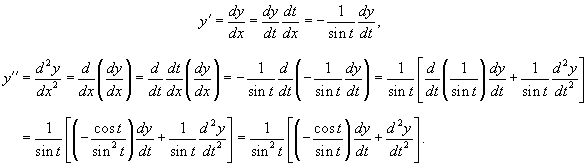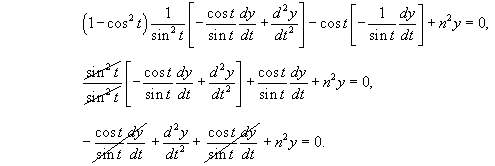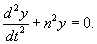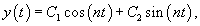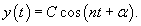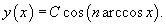
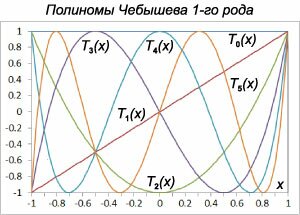
Это уравнение можно преобразовать в более простую форму с помощью подстановки x = cos t. Действительно, в этом случае мы получаем: Следовательно, Подставим выражения для производных в дифференциальное уравнение: В результате дифференциальное уравнение принимает более компактный вид: Общее решение последнего уравнения определяется формулой которую можно записать также в форме Здесь C₁, C₂, C и α − произвольные действительные числа. Для простоты можно положить α = 0. Тогда общее решение исходного уравнения Чебышева будет описываться выражением В этой формуле n означает любое действительное число. В случае, когда n − целое число, данная формула описывает полиномы Чебышева первого рода. Полиномом Чебышева первого рода называется функция где |x| ≤ 1 и n = 0,1,2,3,.... Далее мы покажем, что указанную функцию можно представить в виде алгебраического многочлена. Для n = 0 и n = 1 имеем Полагая x = cos t, можно записать: Поскольку то мы получаем следующую систему рекуррентных соотношений для полиномов Чебышева первого рода: Теперь можно легко вычислить полиномы Чебышева более высокого порядка: и так далее... 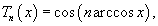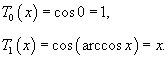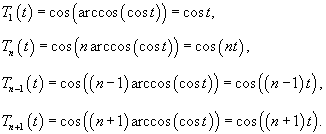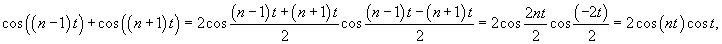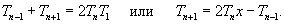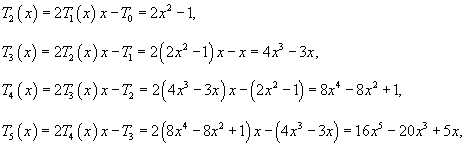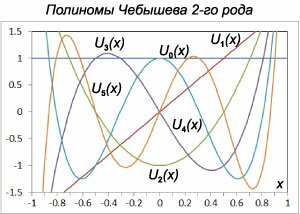Полиномы Чебышева второго рода также можно определить с помощью рекуррентных соотношений: Полиномы Чебышева второго рода являются решениями дифференциального уравнения Чебышева вида Графики полиномов Чебышева первого и второго рода показаны, соответственно, на рисунках 1 и 2.

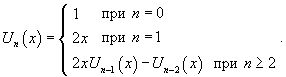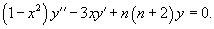
   Пример 1

Найти общее решение уравнения  (1 − x²)y'' − xy' + 2y = 0 при |x| < 1. Данное уравнение является уравнением Чебышева с дробным параметром n = √2. Его общее решение можно записать в тригонометрической форме: где C₁, C₂ − произвольные постоянные. Заметим, что в данном случае решение не выражается через полиномы Чебышева из-за дробного параметра √2.

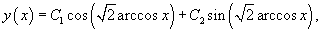   Пример 2

Найти общее решение дифференциального уравнения  (1 − x²)y'' − xy' + 4y = 0 при |x| < 1. Здесь мы имеем дело с уравнением Чебышева с параметром n =2. Поэтому можно прямо записать общее решение в форме: где C₁, C₂ − произвольные постоянные.

Это решение можно выразить через полиномы Чебышева первого рода. Поскольку 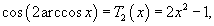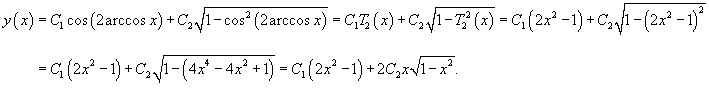то получаем окончательный ответ в следующем виде: