|
Замена переменных в двойных интегралах
|
||||||
|
Для вычисления двойного интеграла
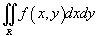 иногда удобнее перейти в другую систему координат. иногда удобнее перейти в другую систему координат.Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции. В новой системе координат вычисление двойного интеграла значительно упрощается. Замена переменных в двойном интеграле описывается формулой 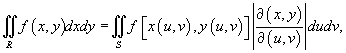 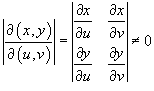 представляет собой так называемый якобиан преобразования представляет собой так называемый якобиан преобразования  , а S − образ области интегрирования R, который можно найти с помощью подстановки , а S − образ области интегрирования R, который можно найти с помощью подстановки 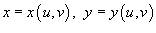 в определение области R. Отметим, что в приведенной выше формуле в определение области R. Отметим, что в приведенной выше формуле 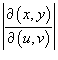 означает абсолютное значение соответствующего определителя. означает абсолютное значение соответствующего определителя.Предполагая, что преобразование координат 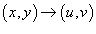 является взаимно-однозначным, обратное соотношение описывается якобианом является взаимно-однозначным, обратное соотношение описывается якобианом
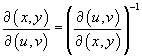 Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:
|
||||||
|
Пример 1
|
||||||
|
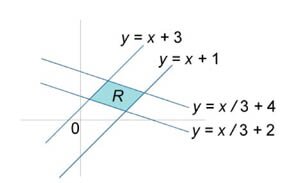
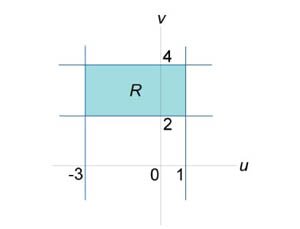
Вычислить двойной интеграл
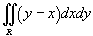 , в котором область определения R ограничена прямыми , в котором область определения R ограничена прямыми 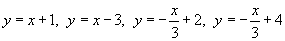 . .
Решение.  , получаем , получаем
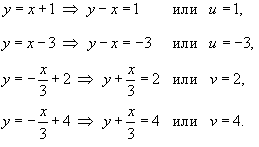
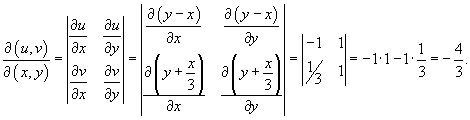 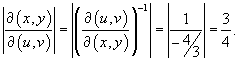 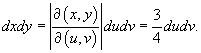 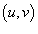 интеграл вычисляется намного легче: интеграл вычисляется намного легче:
 |
||||||
|
Пример 2
|
||||||
|
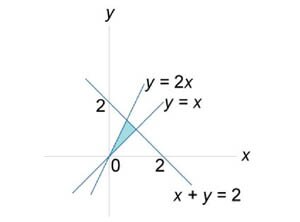
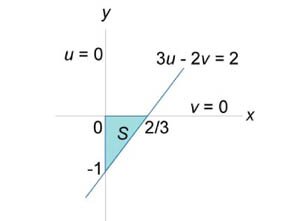
Вычислить двойной интеграл
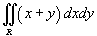 , в котором область интегрирования R ограничена прямыми линиями , в котором область интегрирования R ограничена прямыми линиями 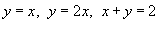 . .
Решение. 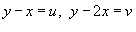 . Выразим . Выразим 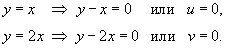
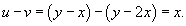 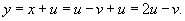 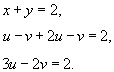 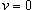 , то , то 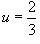 . Соответственно, если . Соответственно, если 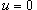 , то , то 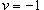 . Область S имеет вид прямоугольного треугольника (рисунок 4 выше). . Область S имеет вид прямоугольного треугольника (рисунок 4 выше).Уравнение стороны 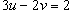 можно переписать в виде можно переписать в виде
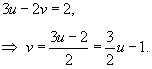 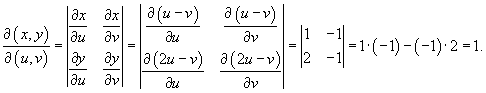 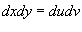 и двойной интеграл становится равным и двойной интеграл становится равным
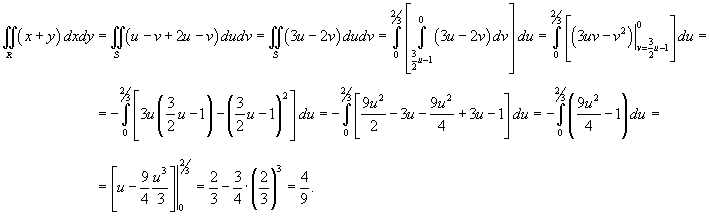 |
||||||
|
Пример 3
|
||||||
|
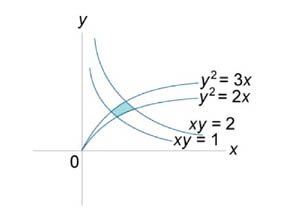
Вычислить интеграл
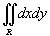 , где область R ограничена параболами , где область R ограничена параболами 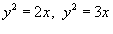 и гиперболами и гиперболами 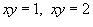 . .
Решение.
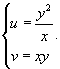 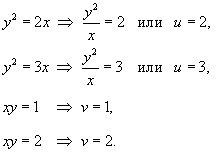 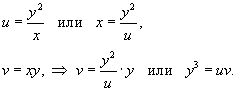 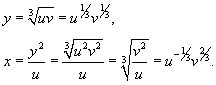 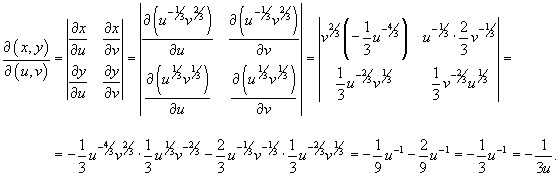 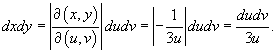 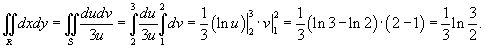 |
||||||
|
Пример 4
|
||||||
|
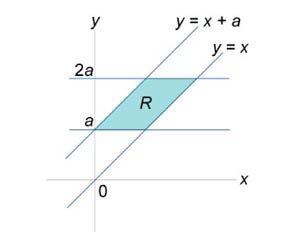
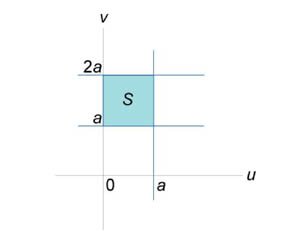
Вычислить интеграл
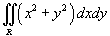 , где область R ограничена прямыми , где область R ограничена прямыми 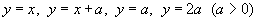 . .
Решение.
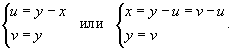 Найдем образ S области R в новых координатах 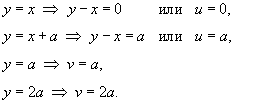 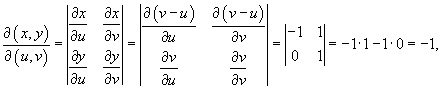 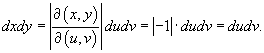 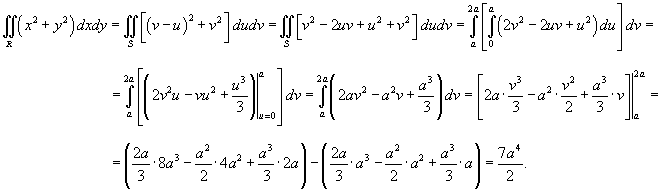 |
||||||
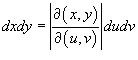 ;
;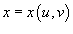 и
и 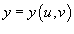 .
.