|
Прогиб балки
|
||||||||||||
|
Балкой называют конструктивный элемент, способный выдерживать большие нагрузки на изгиб. В случае малых прогибов форму балки можно описать линейным дифференциальным уравнением 4-го порядка.
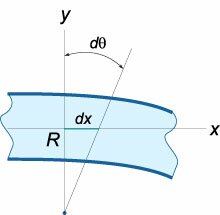
Рассмотрим вывод данного уравнения. При изгибе балки между двумя смежными сечениями, отстоящими друг от друга на расстоянии dx, образуется угол dθ (рисунок 1).
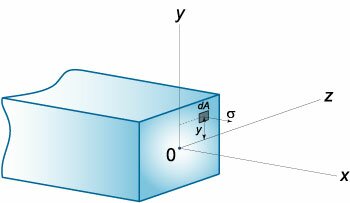
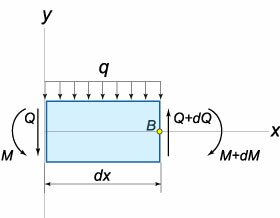
Из геометрии рисунка 1 следует, что 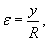 Величина нормального напряжения σ в сечении будет также зависеть от координаты y. Ее можно оценить по закону Гука: 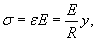 Изгибающий момент 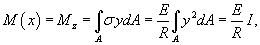 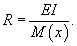 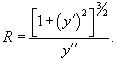 
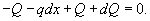 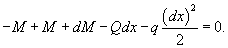  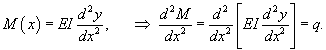 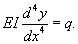 |
||||||||||||
|
Пример 1
|
||||||||||||
|
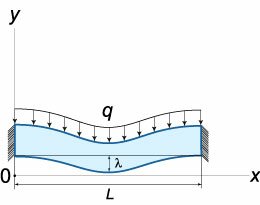
Определить прогиб балки, жестко закрепленной с обоих концов и нагруженной равномерно распределенной силой (рисунок 4).
Решение. Уравнение прогиба балки имеет вид:  При жестком закреплении концов балки справедливы следующие граничные условия: 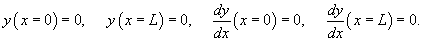 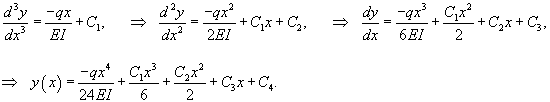 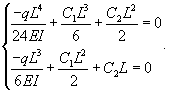 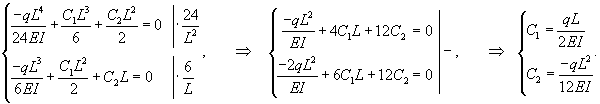 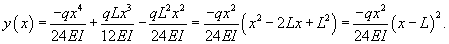 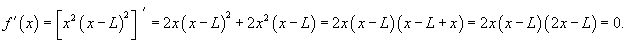 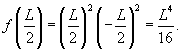 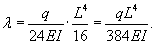 |
||||||||||||
|
Пример 2
|
||||||||||||
|
Тонкий цилиндрический вал длиной L вращается с угловой скоростью ω. При какой скорости ω может произойти разрушение вала? Модуль упругости материала E, масса вала M, радиус сечения a.
Решение.
При вращении вала на него действует центробежная сила, которая пропорциональна отклонению y от оси вращения. При увеличении в некоторой точке деформации y центробежная сила в этой точке также будет возрастать, что приведет к дальнейшему искривлению вала. Неустойчивость такого рода возникает при определенных частотах и может привести к разрушению вала.Исследуем эту задачу с помощью дифференциального уравнения. Базовое уравнение, описывающее деформацию вала, записывается в виде: 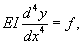 На элемент вала dx действует центробежная сила, равная 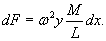 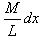 соответствует массе элемента dx, y − прогиб вала, равный радиусу вращения элемента dx. В результате наше дифференциальное уравнение принимает вид: соответствует массе элемента dx, y − прогиб вала, равный радиусу вращения элемента dx. В результате наше дифференциальное уравнение принимает вид:
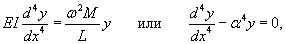 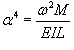 . .Итак, мы получили красивое линейное дифференциальное уравнение четвертого порядка. Найдем корни характеристического уравнения. 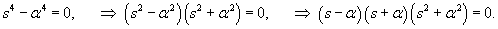 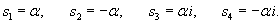 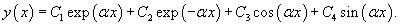
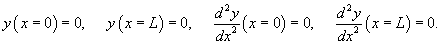 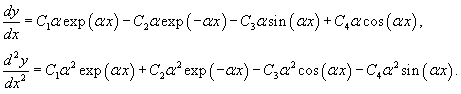 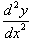 в граничные условия, получаем в граничные условия, получаем
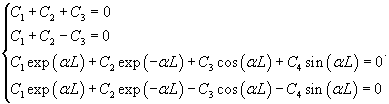 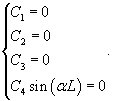 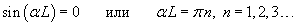 Итак, при  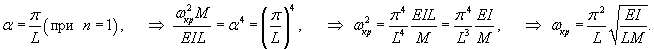 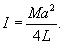 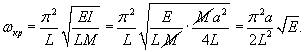 |
||||||||||||