|
Барометрическая формула
|
||||||
|
В данном разделе мы выведем зависимость давления газа P от высоты h над уровнем моря в гравитационном поле Земли.
Возьмем произвольную цилиндрическую колонну газа с площадью сечения S и высотой h. Тогда вес выделенного объема газа будет равен 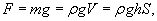 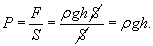 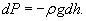
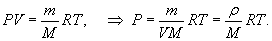 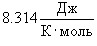 , M − молярная масса, которая для воздуха равна , M − молярная масса, которая для воздуха равна 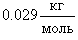 . Отсюда следует, что плотность определяется формулой . Отсюда следует, что плотность определяется формулой
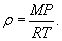 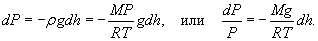 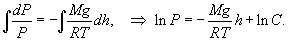 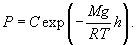 Таким образом, зависимость атмосферного давления от высоты выражается формулой: 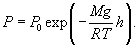 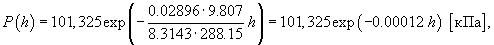 Если давление определяется в миллиметрах ртутного столба (мм рт.ст.), то барометрическая формула принимает вид: 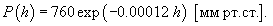 |
||||||
|
Пример 1
|
||||||
|
Определить на какой высоте при стандартных условиях давление воздуха в два раза ниже, чем на уровне моря?
Решение. 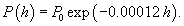 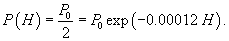 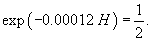 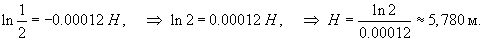 |
||||||
|
Пример 2
|
||||||
|
Найти давление воздуха в шахте на глубине 1 км при температуре 40 градусов Цельсия.
Решение. 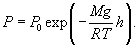 После несложных вычислений находим: 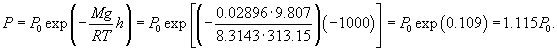 |
||||||

