|
Определение ряда Фурье и типичные примеры
|
||||||
Определение ряда Фурье
Говорят, что функция \(f\left( x \right)\) имеет период \(P,\) если \(f\left( {x + P} \right) = f\left( x \right)\) для всех значений \(x.\) Пусть период функции \(f\left( x \right)\) равен \(2\pi.\) В этом случае достаточно рассмотреть поведение функции в интервале \(\left[ { - \pi ,\pi } \right].\)
Если \({x_0}\) − точка разрыва, то ряд Фурье сходится к значению \[\lim\limits_{\varepsilon \to 0} \frac{1}{2}\left[ {f\left( {{x_0} - \varepsilon } \right) - f\left( {{x_0} + \varepsilon } \right)} \right].\] Ряд Фурье функции \(f\left( x \right)\) представляется в виде \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left\{ {{a_n}\cos nx + {b_n}\sin nx} \right\}} ,\] где коэффициенты Фурье \({{a_0}},\) \({{a_n}}\) и \({{b_n}}\) определяются формулами \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nx dx} ,}\;\; {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nx dx} .} \] Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя \({{a_n}}\) и \({{b_n}}\) новыми переменными \({{d_n}}\) и \({{\varphi_n}}\) или \({{d_n}}\) и \({{\theta_n}},\) где \[ {{d_n} = \sqrt {a_n^2 + b_n^2} ,}\;\; {\tan {\varphi _n} = \frac{{{a_n}}}{{{b_n}}},}\;\; {\tan {\theta _n} = \frac{{{b_n}}}{{{a_n}}},} \] можно, соответственно, записать \[ {f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{d_n}\sin \left( {nx + {\varphi _n}} \right)} \;\;\text{или}\;\;} {f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{d_n}\cos\left( {nx + {\theta _n}} \right)} .} \]
Разложение в ряд Фурье четных и нечетных функций
Разложение в ряд Фурье четной функции \(f\left( x \right)\) с периодом \(2\pi\) не содержит синусов и имеет вид \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} ,\] где коэффициенты Фурье определяются выражениями \[ {{a_0} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} .} \] Аналогично, разложение в ряд Фурье нечетной функции \(f\left( x \right),\) имеющей период \(2\pi,\) содержит только синусы и имеет вид \[f\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin nx} ,\] где коэффициенты \({{b_n}}\) равны \[{b_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\sin nxdx} .\] Ниже мы рассмотрим некоторые типичные примеры разложения функций с периодом \(2\pi\) в ряд Фурье, предполагая, что такие разложения существуют и сходятся к заданной функции. |
||||||
|
Пример 1
|
||||||
|
Пусть функция \(f\left( x \right)\) имеет период \(2\pi\) и раскладывается в ряд Фурье: \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left\{ {{a_n}\cos nx + {b_n}\sin nx} \right\}} .\] Вычислить коэффициенты \({{a_0}},\) \({{a_n}}\) и \({{b_n}}.\)
Решение. В случае \(m = n\) получаем \[\require{cancel} {\int\limits_{ - \pi }^\pi {\sin nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\sin 2mx + \sin 0} \right]dx} ,}\;\; {\Rightarrow \int\limits_{ - \pi }^\pi {{\sin^2}mxdx} = \frac{1}{2}\left[ {\left. {\left( { - \frac{{\cos 2mx}}{{2m}}} \right)} \right|_{ - \pi }^\pi } \right] } = {\frac{1}{{4m}}\left[ { - \cancel{\cos \left( {2m\pi } \right)} + \cancel{\cos \left( {2m\left( { - \pi } \right)} \right)}} \right] = 0;} \] \[ {\int\limits_{ - \pi }^\pi {\cos nx\cos mxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\cos 2mx + \cos 0} \right]dx} ,}\;\; {\Rightarrow \int\limits_{ - \pi }^\pi {{\cos^2}mxdx} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{\sin 2mx}}{{2m}}} \right)} \right|_{ - \pi }^\pi + 2\pi } \right] } = {\frac{1}{{4m}}\left[ {\sin \left( {2m\pi } \right) - \sin \left( {2m\left( { - \pi } \right)} \right)} \right] + \pi = \pi .} \] Таким образом, \[ {\int\limits_{ - \pi }^\pi {f\left( x \right)\cos mxdx} = {a_m}\pi ,}\;\; {\Rightarrow {a_m} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos mxdx} ,}\;\; {m = 1,2,3, \ldots } \] Аналогично, умножая ряд Фурье на \(\sin mx\) и интегрируя почленно, получим выражение для \({{b_m}}:\) \[ {{b_m} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin mxdx} ,}\;\; {m = 1,2,3, \ldots } \] Переписывая формулы для \({{a_n}},\) \({{b_n}},\) запишем окончательные выражения для коэффициентов Фурье: \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} ,}\;\; {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} .} \] |
||||||
|
Пример 2
|
||||||
|
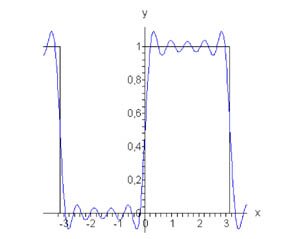
Найти разложение в ряд Фурье прямоугольной функции с периодом \(2\pi,\) определенной в интервале \(\left[ { - \pi ,\pi } \right]:\) \[ f\left( x \right) = \begin{cases} 0, & \text{если} & - \pi \le x \le 0 \\ 1, & \text{если} & 0 < x \le \pi \end{cases}. \]
Решение.
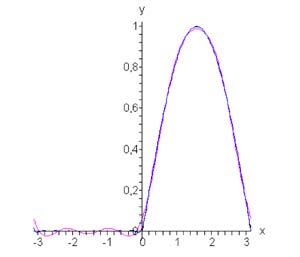
Вычислим сначала \({{a_0}}:\) \[ {{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)dx} } = {\frac{1}{\pi }\int\limits_0^\pi {1dx} } = {\frac{1}{\pi } \cdot \pi = 1.} \] Определим теперь коэффициенты Фурье при \(n \ne 0:\) \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\cos nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {1 \cdot \cos nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{\pi n}} \cdot 0 = 0,} \] \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {1 \cdot \sin nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\cos nx}}{n}} \right)} \right|_0^\pi } \right] } = { - \frac{1}{{\pi n}} \cdot \left( {\cos n\pi - \cos 0} \right) } = {\frac{{1 - \cos n\pi }}{{\pi n}}.} \] Поскольку \(\cos n\pi = {\left( { - 1} \right)^n},\) то можно записать \[{b_n} = \frac{{1 - {{\left( { - 1} \right)}^n}}}{{\pi n}}.\] Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид \[f\left( x \right) = \frac{1}{2} + \sum\limits_{n = 1}^\infty {\frac{{1 - {{\left( { - 1} \right)}^n}}}{{\pi n}}\sin nx} .\] Можно легко вычислить несколько первых членов разложения. Полагая, например, \(n = 5,\) получаем \[ {f\left( x \right) = \frac{1}{2} + \frac{{1 - \left( { - 1} \right)}}{\pi }\sin x } + {\frac{{1 - {{\left( { - 1} \right)}^2}}}{{2\pi }}\sin 2x } + {\frac{{1 - {{\left( { - 1} \right)}^3}}}{{3\pi }}\sin 3x } + {\frac{{1 - {{\left( { - 1} \right)}^4}}}{{4\pi }}\sin 4x } + {\frac{{1 - {{\left( { - 1} \right)}^5}}}{{5\pi }}\sin 5x + \ldots } = {\frac{1}{2} + \frac{2}{\pi }\sin x } + {\frac{2}{{3\pi }}\sin 3x } + {\frac{2}{{5\pi }}\sin 5x + \ldots } \] На рисунке \(1\) представлены график данной функции и ее аппроксимация рядом Фурье при \(n = 10.\)
|
||||||
|
Пример 3
|
||||||
|
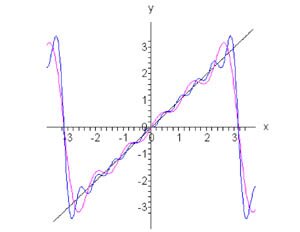
Найти разложение в ряд Фурье для пилообразной функции, определенной в интервале \(\left[ { - \pi ,\pi } \right]\) и имеющей период \(2\pi.\)
Решение. Поскольку функция нечетная (рисунок \(2\)), то \({a_0} = {a_n} = 0.\) \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {x\sin nxdx} .} \] Для вычисления последнего интеграла используем формулу интегрирования по частям: \[\int\limits_{ - \pi }^\pi {udv} = \left. {\left( {uv} \right)} \right|_{ - \pi }^\pi - \int\limits_{ - \pi }^\pi {vdu} .\] Пусть \(u = x,\;dv = \sin nxdx.\) Тогда \(du = dx,\;v = \int {\sin nxdx} = - \large\frac{{\cos nx}}{n}\normalsize,\) и интеграл будет равен \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {x\sin nxdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\cos nx}}{n}} \right)} \right|_{ - \pi }^\pi - \int\limits_{ - \pi }^\pi {\left( { - \frac{{\cos nx}}{n}} \right)dx} } \right] } = {\frac{1}{\pi }\left[ {\left( { - \frac{{\pi \cos n\pi }}{n} + \frac{{\left( { - \pi } \right)\cos \left( { - n\pi } \right)}}{n}} \right) + \frac{1}{n}\int\limits_{ - \pi }^\pi {\cos nxdx} } \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \left. {\left( {\frac{{\sin nx}}{n}} \right)} \right|_{ - \pi }^\pi } \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \frac{1}{n}\left( {\sin n\pi - \sin \left( { - n\pi } \right)} \right)} \right] } = {\frac{1}{{n\pi }}\left[ { - 2\pi \cos n\pi + \frac{{2\sin n\pi }}{n}} \right] } = {\frac{2}{{n\pi }}\left[ {\frac{{\sin n\pi }}{n} - \pi \cos n\pi } \right].} \] Подставляя \(\sin n\pi = 0\) и \(\cos n\pi = {\left( { - 1} \right)^n}\) для всех натуральных значений \(n,\) получаем \[ {{b_n} = \frac{2}{{n\pi }}\left( { - \pi {{\left( { - 1} \right)}^n}} \right) } = { - \frac{2}{n}{\left( { - 1} \right)^n} } = {\frac{2}{n}{\left( { - 1} \right)^{n + 1}}.} \] Следовательно, разложение в ряд Фурье прилообразной волны имеет вид (рисунок \(2\) выше) \[x = \sum\limits_{n = 1}^\infty {\frac{2}{n}{{\left( { - 1} \right)}^{n + 1}}\sin nx} .\] |
||||||
|
Пример 4
|
||||||
|
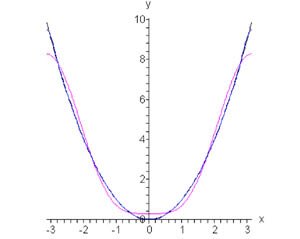
Предположим, что \(f\left( x \right)\) является периодической функцией с периодом \(2\pi.\) Пусть \(f\left( x \right) = {x^2}\) для \(x \in \left[ { - \pi ,\pi } \right].\) Найти разложение Фурье для заданной параболической функции.
Решение.
|
||||||
|
Пример 5
|
||||||
|
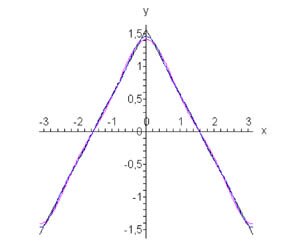
Найти ряд Фурье для треугольной волны \[ f\left( x \right) = \begin{cases} \frac{\pi }{2} + x, & \text{если} & - \pi \le x \le 0 \\ \frac{\pi }{2} - x, & \text{если} & 0 < x \le \pi \end{cases}, \] определенной в интервале \(\left[ { - \pi ,\pi } \right].\)
Решение. Так как функция \(f\left( x \right)\) четная, то коэффициенты Фурье \({b_n}\) равны нулю. Таким образом, окончательное разложение треугольной волны в ряд Фурье выглядит следующим образом (см. рис. \(4\)): \[f\left( x \right) = \frac{4}{\pi }\sum\limits_{k = 0}^\infty {\frac{{\cos \left( {2k + 1} \right)x}}{{{{\left( {2k + 1} \right)}^2}}}} .\] |
||||||
|
Пример 6
|
||||||
|
Найти разложение в ряд Фурье для функции \[ f\left( x \right) = \begin{cases} 0, & \text{если} & - \pi \le x \le 0 \\ \sin x, & \text{если} & 0 < x \le \pi \end{cases}, \] заданной в интервале \(\left[ { - \pi ,\pi } \right].\)
Решение.
|
||||||
|
Пример 7
|
||||||
|
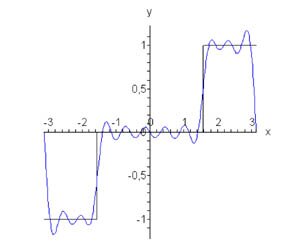
Найти ряд Фурье для функции \[ f\left( x \right) = \begin{cases} -1, & \text{если} & - \pi \le x \le - \frac{\pi }{2} \\ 0, & \text{если} & - \frac{\pi }{2} \lt x \le \frac{\pi }{2} \\ 1, & \text{если} & \frac{\pi }{2} < x \le \pi \end{cases}, \] определенной в интервале \(\left[ { - \pi ,\pi } \right].\)
Решение. Определим коэффициенты разложения \({b_n}:\) \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( x \right)\sin nxdx} } = {\frac{1}{\pi }\left[ {\int\limits_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} {\left( { - \sin nx} \right)dx} + \int\limits_{\large\frac{\pi }{2}\normalsize}^\pi {\sin nxdx} } \right] } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{\cos nx}}{n}} \right)} \right|_{ - \pi }^{ - \large\frac{\pi }{2}\normalsize} - \left. {\left( {\frac{{\cos nx}}{n}} \right)} \right|_{\large\frac{\pi }{2}\normalsize}^\pi } \right] } = {\frac{1}{{\pi n}}\left[ {\cos\left( { - \frac{{n\pi }}{2}} \right) - \cos \left( { - n\pi } \right) - \cos n\pi + \cos \frac{{n\pi }}{2}} \right] } = {\frac{1}{{\pi n}}\left[ {\cos\frac{{n\pi }}{2} - \cos n\pi - \cos n\pi + \cos \frac{{n\pi }}{2}} \right] } = {\frac{2}{{\pi n}}\left( {\cos\frac{{n\pi }}{2} - \cos n\pi } \right).} \] Таким образом, разложение в ряд Фурье определяется формулой \[f\left( x \right) = \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{1}{n}\left( {\cos\frac{{n\pi }}{2} - \cos n\pi } \right)\sin nx} .\] На рисунке \(6\) представлен график исходной прямоугольной функции и ее Фурье аппроксимации при \(n = 10.\) |
||||||