Формула Грина

Пусть в плоскости \(Oxy\) задана область \(R,\) ограниченная замкнутой, кусочно-непрерывной и гладкой кривой \(C.\) Предположим, что в некоторой области, содержащей \(R,\) задана непрерывная векторная функция \[\mathbf{F} = P\left( {x,y} \right)\mathbf{i} + Q\left( {x,y} \right)\mathbf{j}\] с непрерывными частными производными первого порядка \(\large\frac{{\partial P}}{{\partial y}}\normalsize, \large\frac{{\partial Q}}{{\partial x}}\normalsize.\) Тогда справедлива формула Грина \[ {\iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\oint\limits_C {Pdx + Qdy} ,} \] где символ \(\oint\limits_C {} \) указывает, что кривая (контур) \(C\) является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.

Если \(Q = x,\) \(P = -y,\) то формула Грина принимает вид \[S = \iint\limits_R {dxdy} = \frac{1}{2}\oint\limits_C {xdy - ydx} ,\] где \(S\) − это площадь области \(R,\) ограниченной контуром \(C.\)

Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля.

Пусть векторное поле описывается функцией \[\mathbf{F} = P\left( {x,y,z} \right)\mathbf{i} + Q\left( {x,y,z} \right)\mathbf{j} + R\left( {x,y,z} \right)\mathbf{k}.\] Ротором или вихрем векторного поля \(\mathbf{F}\) называется вектор, обозначаемый \(\text{rot}\,\mathbf{F}\) или \(\nabla \times \mathbf{F}\) и равный \[ {\text{rot}\,\mathbf{F} = \nabla \times \mathbf{F} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ {\frac{\partial }{{\partial x}}}&{\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial z}}}\\ P&Q&R \end{array}} \right| } = {{\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right)\mathbf{i} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right)\mathbf{j} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)\mathbf{k}.}} \] Формула Грина в векторной форме записывается в виде \[ {\iint\limits_R {\left( \text{rot}\,\mathbf{F} \right) \cdot \mathbf{k}\,dxdy} } = {\oint\limits_C {\mathbf{F} \cdot d\mathbf{r}} .} \] Заметим, что формула Грина вытекает из теоремы Стокса при переходе от трехмерного случая к случаю двух координат.

   Пример 1

Используя формулу Грина, вычислить интеграл \(\oint\limits_C {xydx + \left( {x + y} \right)dy} ,\) где кривая \(C\) − окружность радиуса \(R.\) Запишем компоненты векторного поля: \[P\left( {x,y} \right) = xy,\;\;Q\left( {x,y} \right) = x + y.\] С помощью формулы Грина \[ {\iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\oint\limits_C {Pdx + Qdy} } \] преобразуем криволинейный интеграл в двойной: \[ {I = \oint\limits_C {xydx + \left( {x + y} \right)dy} } = {\iint\limits_R {\left( {\frac{{\partial \left( {x + y} \right)}}{{\partial x}} - \frac{{\partial \left( {xy} \right)}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {1 - x} \right)dxdy} .} \] Переходя к полярным координатам, находим искомый интеграл: \[ {I = \int\limits_R {\left( {1 - x} \right)dxdy} } = {\int\limits_0^{2\pi } {\int\limits_0^1 {\left( {1 - r\cos \theta } \right)rdrd\theta } } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^1 {\left( {r - {r^2}\cos \theta } \right)dr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\left. {\left( {\frac{{{r^2}}}{2} - \frac{{{r^3}}}{3}\cos \theta } \right)} \right|_{r = 0}^1} \right]d\theta } } = {\int\limits_0^{2\pi } {\left( {\frac{1}{2} - \frac{{\cos \theta }}{3}} \right)d\theta } } = {\left. {\left( {\frac{\theta }{2} - \frac{{\sin \theta }}{3}} \right)} \right|_0^{2\pi } = \pi .} \]

   Пример 2

Используя формулу Грина, найти интеграл \(\oint\limits_C {\left( {x - y} \right)dx + \left( {x + y} \right)dy},\) где кривая \(C\) представляет собой окружность, заданную уравнением \({x^2} + {y^2} = {a^2}.\) Сначала запишем компоненты векторного поля \[P = x - y,\;\;Q = x + y\] и определим частные производные: \[ {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( {x + y} \right)}}{{\partial x}} = 1,}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {x - y} \right)}}{{\partial x}} = - 1.} \] Следовательно, интеграл можно записать в следующем виде \[ {I = \oint\limits_C {\left( {x - y} \right)dx + \left( {x + y} \right)dy} } = {\iint\limits_R {\left( {1 - \left( { - 1} \right)} \right)dxdy} } = {2\iint\limits_R {dxdy} .} \] В последнем равенстве двойной интеграл \(\iint\limits_R {dxdy} \) численно равен площади круга \({x^2} + {y^2} = {a^2},\) то есть \(\pi {a^2}.\) Тогда интеграл равен \[I = 2\iint\limits_R {dxdy} = 2\pi {a^2}.\]

   Пример 3

Используя формулу Грина, вычислить интеграл \(\oint\limits_C {{x^2}ydx - x{y^2}dy} .\) Кривая \(C\) представляет собой окружность \({x^2} + {y^2} = {a^2}\) (рисунок \(1\)), обход которой производится против часовой стрелки. Запишем компоненты векторного поля и их производные: \[ {P\left( {x,y} \right) = {x^2}y,}\;\; {Q\left( {x,y} \right) = - x{y^2},}\;\; {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( { - x{y^2}} \right)}}{{\partial x}} = - {y^2},}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {{x^2}y} \right)}}{{\partial y}} = {x^2}.} \] Тогда \[ {I = \oint\limits_C {{x^2}ydx - x{y^2}dy} } = {\iint\limits_R {\left( { - {y^2} - {x^2}} \right)dxdy} } = { - \iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} ,} \] где \(R\) − круг радиуса \(a\) с центром в начале координат. Переходя к полярным координатам, находим искомый интеграл: \[ {I = - \iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} } = { - \int\limits_0^{2\pi } {d\theta } \int\limits_0^a {\left( {{r^2}{{\cos }^2}\theta + {r^2}{\sin^2}\theta } \right)rdr} } = { - \int\limits_0^{2\pi } {d\theta } \int\limits_0^a {{r^3}dr} } = { - 2\pi \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^a} \right] } = { - \frac{{\pi {a^4}}}{2}.} \]

   Пример 4

Используя формулу Грина, найти интеграл \(\oint\limits_C {\left( {x + y} \right)dx - \left( {x - y} \right)dy} ,\) где кривая \(C\) представляет собой эллипс \(\large\frac{{{x^2}}}{{{a^2}}}\normalsize + \large\frac{{{y^2}}}{{{b^2}}}\normalsize = 1\) (рисунок \(2\)). Применим формулу Грина \[ {\oint\limits_C {Pdx + Qdy} } = { \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} . } \] Очевидно, здесь \[ {P = x + y,}\;\; {Q = - \left( {x - y} \right),}\;\; {\frac{{\partial Q}}{{\partial x}} = - 1,}\;\; {\frac{{\partial P}}{{\partial y}} = 1.} \] Следовательно, \[ {I = \oint\limits_C {\left( {x + y} \right)dx - \left( {x - y} \right)dy} } = {\iint\limits_R {\left( { - 1 - 1} \right)dxdy} } = { - 2\iint\limits_R {dxdy} .} \] Поскольку двойной интеграл \(\iint\limits_R {dxdy} \) численно равен площади эллипса \(\pi ab,\) то интеграл равен \[I = - 2\iint\limits_R {dxdy} = - 2\pi ab.\]

   Пример 5

С помощью формулы Грина вычислить интеграл \(\oint\limits_C {{y^2}dx + {{\left( {x + y} \right)}^2}dy}, \) где контур \(C\) представляет собой треугольник \(ABC\) с вершинами \(A\left( {a,0} \right),\) \(B\left( {a,a} \right),\) \(D\left( {0,a} \right)\) (рисунок \(3\)). В заданном криволинейном интеграле \(P = {y^2},\) \(Q = {\left( {x + y} \right)^2},\) так что \[ {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( {{{\left( {x + y} \right)}^2}} \right)}}{{\partial x}} = 2\left( {x + y} \right),}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {{y^2}} \right)}}{{\partial y}} = 2y.} \] Тогда по формуле Грина получаем \[ {I = \oint\limits_C {{y^2}dx + {{\left( {x + y} \right)}^2}dy} } = {\iint\limits_R {\left[ {2\left( {x + y} \right) - 2y} \right]dxdy} } = {2\iint\limits_R {xdxdy} .} \] Уравнение стороны \(AD\) имеет вид \(y = -x + a.\) Следовательно, полученный двойной интеграл вычисляется следующим образом: \[ {I = 2\iint\limits_R {xdxdy} } = {2\int\limits_0^a {\left[ {\int\limits_{ - x + a}^a {dy} } \right]xdx} } = {2\int\limits_0^a {\left[ {\left. y \right|_{ - x + a}^a} \right]xdx} } = {2\int\limits_0^a {\left[ {a - \left( { - x + a} \right)} \right]xdx} } = {2\int\limits_0^a {{x^2}dx} } = {2\left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^a} \right] } = {\frac{{2{a^3}}}{3}.} \]

   Пример 6

С помощью формулы Грина найти интеграл \(\oint\limits_C {\left( {y - {x^2}} \right)dx - \left( {x + {y^2}} \right)dy} .\) Контур \(C\) ограничивает сектор круга радиусом \(a,\) лежащий в первом квадранте (рисунок \(4\)). В соответствии с формулой Грина \[ {\oint\limits_C {Pdx + Qdy} } = { \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy}, } \] находим \[ {P = y - {x^2},}\;\; {Q = - \left( {x + {y^2}} \right),}\;\; {\frac{{\partial Q}}{{\partial x}} = - \frac{{\partial \left( {x + {y^2}} \right)}}{{\partial x}} = - 1,}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {y - {x^2}} \right)}}{{\partial y}} = 1.} \] Следовательно, \[ {I = \oint\limits_C {\left( {y - {x^2}} \right)dx - \left( {x + {y^2}} \right)dy} } = {\iint\limits_R {\left( { - 1 - 1} \right)dxdy} } = { - 2\iint\limits_R {dxdy} .} \] Переходя к полярным координатам, вычисляем интеграл \[ {I = - 2\iint\limits_R {dxdy} } = { - 2\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\theta } \int\limits_0^a {rdr} } = { - 2 \cdot \frac{\pi }{2} \cdot \left[ {\left. {\left( {\frac{{{r^2}}}{2}} \right)} \right|_0^a} \right] } = { - \frac{{\pi {a^2}}}{2}.} \]

   Пример 7

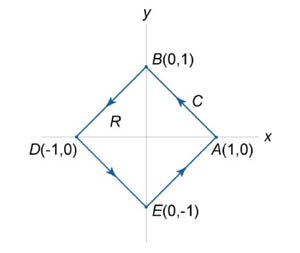
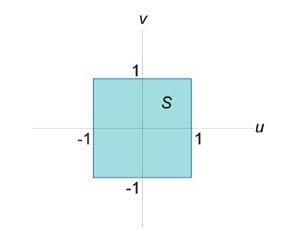
Вычислить интеграл \(\oint\limits_C {\large\frac{{dx - dy}}{{x + y}}\normalsize} \) с использованием формулы Грина. Контур интегрирования \(C\) представляет собой квадрат с вершинами в точках \(A\left( {1,0} \right),\) \(B\left( {0,1} \right),\) \(D\left( {-1,0} \right),\) \(E\left( {0,-1} \right)\) (рисунок \(5\)). В соответствии с формулой Грина запишем \[ {P = \frac{1}{{x + y}},}\;\; {Q = - \frac{1}{{x + y}},}\;\; {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( { - \frac{1}{{x + y}}} \right)}}{{\partial x}} = \frac{1}{{{{\left( {x + y} \right)}^2}}},}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {\frac{1}{{x + y}}} \right)}}{{\partial y}} = - \frac{1}{{{{\left( {x + y} \right)}^2}}}.} \] Следовательно, \[ {I = \oint\limits_C {\frac{{dx - dy}}{{x + y}}} } = {\iint\limits_R {\left( {\frac{1}{{{{\left( {x + y} \right)}^2}}} + \frac{1}{{{{\left( {x + y} \right)}^2}}}} \right)dxdy} } = {2\iint\limits_R {\frac{{dxdy}}{{{{\left( {x + y} \right)}^2}}}} .} \] Найдем уравнения сторон квадрата: \[AB:y = - x + 1,\] \[BD:y = x + 1,\] \[DE:y = - x - 1,\] \[EA:y = x - 1.\] Далее удобно ввести новые переменные. Пусть \(u = y + x,\) \(v = y - x.\) Уравнения сторон квадрата записываются через новые переменные \(u\) и \(v\) в виде \[y = - x + 1,\;\; \Rightarrow y + x = 1,\;\; \Rightarrow u = 1,\] \[y = x + 1,\;\; \Rightarrow y - x = 1,\;\; \Rightarrow v = 1,\] \[y = - x - 1,\;\; \Rightarrow y + x = - 1,\;\; \Rightarrow u = - 1,\] \[y = x - 1,\;\; \Rightarrow y - x = - 1,\;\; \Rightarrow v = - 1.\] Как видно, образ \(S\) первоначальной области интегрирования \(R\) является "более симпатичным" квадратом (рисунок \(6\)). Найдем якобиан обратного преобразования координат: \[ {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}} } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial x}}}&{\frac{{\partial u}}{{\partial y}}}\\ {\frac{{\partial v}}{{\partial x}}}&{\frac{{\partial v}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {y + x} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y + x} \right)}}{{\partial y}}}\\ {\frac{{\partial \left( {y - x} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y - x} \right)}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} 1&1\\ { - 1}&1 \end{array}} \right| = 2.} \] Соответственно, абсолютное значение якобиана прямого преобразования равно \[ {\left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right| } = {\left| {{{\left( {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}}} \right)}^{ - 1}}} \right| = \frac{1}{2}.} \] Тогда \[dxdy = \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dudv = \frac{1}{2}dudv,\] и интеграл имеет значение \[ {I = 2\iint\limits_R {\frac{{dxdy}}{{{{\left( {x + y} \right)}^2}}}} } = {2\iint\limits_S {\frac{{\frac{1}{2}dudv}}{{{u^2}}}} } = {\iint\limits_S {\frac{{dudv}}{{{u^2}}}} } = {\int\limits_{ - 1}^1 {dv} \int\limits_{ - 1}^1 {\frac{{du}}{{{u^2}}}} } = {\left[ {\left. v \right|_{ - 1}^1} \right] \cdot \left[ {\left. {\left( { - \frac{1}{u}} \right)} \right|_{ - 1}^1} \right] } = {\left[ {1 - \left( { - 1} \right)} \right] \cdot \left[ { - 1 - \left( { - 1} \right)} \right] = - 4.} \]

   Пример 8

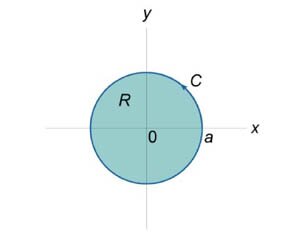
Вычислить интеграл \(\oint\limits_C {\sqrt {{x^2} + {y^2}} dx + y\left[ {xy + \ln \left( {x + \sqrt {{x^2} + {y^2}} } \right)} \right]dy} \) с помощью формулы Грина. Контур интегрирования \(C\) представляет собой окружность \({x^2} + {y^2} = {a^2}\) (рисунок \(7\)). Компоненты векторного поля и их частные производные равны \[ {P = \sqrt {{x^2} + {y^2}} ,}\;\; {Q = y\left[ {xy + \ln \left( {x + \sqrt {{x^2} + {y^2}} } \right)} \right],} \] \[ {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \sqrt {{x^2} + {y^2}} }}{{\partial y}} } = {\frac{y}{{\sqrt {{x^2} + {y^2}} }},} \] \[ {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left\{ {y\left[ {xy + \ln \left( {x + \sqrt {{x^2} + {y^2}} } \right)} \right]} \right\}}}{{\partial x}} } = {y\left( {y + \frac{{1 + \frac{{2x}}{{2\sqrt {{x^2} + {y^2}} }}}}{{x + \sqrt {{x^2} + {y^2}} }}} \right) } = {y\left( {y + \frac{{\frac{{x + \sqrt {{x^2} + {y^2}} }}{{\sqrt {{x^2} + {y^2}} }}}}{{x + \sqrt {{x^2} + {y^2}} }}} \right) } = {y\left( {y + \frac{1}{{\sqrt {{x^2} + {y^2}} }}} \right) } = {{y^2} + \frac{y}{{\sqrt {{x^2} + {y^2}} }}.} \] Тогда по формуле Грина получаем \[ {I = \oint\limits_C {\sqrt {{x^2} + {y^2}} dx + y\left[ {xy + \ln \left( {x + \sqrt {{x^2} + {y^2}} } \right)} \right]dy} } = {\iint\limits_R {\left( {{y^2} + \frac{y}{{\sqrt {{x^2} + {y^2}} }} - \frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)dxdy} } = {\iint\limits_R {{y^2}dxdy} .} \] Для вычисления двойного интеграла удобно перейти к полярным координатам. \[ {I = \iint\limits_R {{y^2}dxdy} } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^a {{r^2}{{\sin }^2}\theta \cdot rdr} } \right]d\theta } } = {\int\limits_0^{2\pi } {{{\sin }^2}\theta d\theta } \int\limits_0^a {{r^3}dr} .} \] Здесь \[ {\int\limits_0^{2\pi } {{{\sin }^2}\theta d\theta } } = {\int\limits_0^{2\pi } {\frac{{1 - \cos 2\theta }}{2}d\theta } } = {\frac{1}{2}\left[ {\left. {\left( {\theta - \frac{{\sin 2\theta }}{2}} \right)} \right|_0^{2\pi }} \right] } = {\frac{1}{2} \cdot 2\pi = \pi ,} \] \[ {\int\limits_0^a {{r^3}dr} } = {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^a } = {\frac{{{a^4}}}{4}.} \] Таким образом, интеграл равен \[I = \frac{{\pi {a^4}}}{4}.\]

   Пример 9

Найти площадь области \(R,\) ограниченной астроидой \(x = a\,{\cos ^3}t,\) \(y = a\,{\sin ^3}t,\) \(0 \le t \le 2\pi .\) Вычислим площадь заданной области с использованием криволинейного интеграла по формуле \({\large\frac{1}{2}\normalsize}\oint\limits_C {xdy - ydx} .\) Запишем данную формулу в параметрическом виде: \[S = \frac{1}{2}\int\limits_\alpha ^\beta {\left( {x\left( t \right)\frac{{dy}}{{dt}} - y\left( t \right)\frac{{dx}}{{dt}}} \right)dt} .\] Подставляя сюда уравнения астроиды, получаем \[ {S = \frac{1}{2}\int\limits_\alpha ^\beta {\left[ {a\,{{\cos }^3}t \cdot \frac{{d\left( {a\,{{\sin }^3}t} \right)}}{{dt}} - a\,{{\sin }^3}t \cdot \frac{{d\left( {a\,{{\cos }^3}t} \right)}}{{dt}}} \right]dt} } = {\frac{1}{2}\int\limits_0^{2\pi } {\left[ {a\,{{\cos }^3}t \cdot 3a\,{{\sin }^2}t\cos t - a\,{{\sin }^3}t \cdot 3a\,{{\cos }^2}t\left( { - \sin t} \right)} \right]dt} } = {\frac{{3{a^2}}}{2}\int\limits_0^{2\pi } {\left[ {{{\cos }^4}t\,{{\sin }^2}t + {{\sin }^4}t\,{{\cos }^2}t} \right]dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {\left[ {4\,{\sin^2}t\,{{\cos }^2}t\left( {{{\cos }^2}t + {{\sin }^2}t} \right)} \right]dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {{{\left( {\sin 2t} \right)}^2}dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {\frac{{1 - \cos 4t}}{2}dt} } = {\frac{{3{a^2}}}{{16}}\int\limits_0^{2\pi } {\left( {1 - \cos 4t} \right)dt} } = {\frac{{3{a^2}}}{{16}}\left[ {\left. {\left( {t - \frac{{\sin 4t}}{4}} \right)} \right|_0^{2\pi }} \right] } = {\frac{{3{a^2}}}{{16}} \cdot 2\pi } = {\frac{{3{a^2}\pi }}{8}.} \]

   Пример 10

Проверить формулу Грина для векторного поля \(\mathbf{F}\left( {P,Q} \right) = \left( {{x^2}{y^2},x{y^2}} \right)\) и области интегрирования \(R,\) имеющей форму круга радиусом \(2\) с центром в начале координат. Вычислим сначала криволинейный интеграл для данного векторного поля. Контуром интегрирования будет служить соответствующая окружность − граница области \(R.\) \[{I_1} = \oint\limits_C {Pdx + Qdy} = \oint\limits_C {{x^2}{y^2}dx + x{y^2}dy} .\] Используя параметрические уравнения окружности \[ {x = 2\cos t,}\;\; {y = 2\sin t,}\;\; {0 \le t \le 2\pi ,} \] получаем \[ {{I_1} = \int\limits_0^{2\pi } {\left[ {{{\left( {2\cos t} \right)}^2} \cdot {{\left( {2\sin t} \right)}^2} \cdot \frac{{d\left( {2\cos t} \right)}}{{dt}} + 2\cos t \cdot {{\left( {2\sin t} \right)}^2} \cdot \frac{{d\left( {2\sin t} \right)}}{{dt}}} \right]dt} } = {\int\limits_0^{2\pi } {\left[ {16\,{{\cos }^2}t\,{{\sin }^2}t \cdot \left( { - 2\sin t} \right) + 8\cos t\,{{\sin }^2}t \cdot 2\cos t} \right]dt} } = {\int\limits_0^{2\pi } {\left[ {16\,{{\cos }^2}t\,{{\sin }^2}t\left( {1 - 2\sin t} \right)} \right]dt} } = {4\int\limits_0^{2\pi } {{{\left( {\sin 2t} \right)}^2}\left( {1 - \sin 2t} \right)dt} } = {4\int\limits_0^{2\pi } {\frac{{1 - \cos 4t}}{2} \cdot \left( {1 - \sin 2t} \right)dt} } = {2\int\limits_0^{2\pi } {\left( {1 - \cos 4t - \sin 2t + \sin 2t\cos 4t} \right)dt} } = {2\int\limits_0^{2\pi } {\left[ {1 - \cos 4t - \sin 2t + \frac{1}{2}\left( {\sin 6t + \sin \left( { - 2t} \right)} \right)} \right]dt} .} \] Здесь мы воспользовались тригонометрической формулой \[ {\sin \alpha \cos \beta } = {\frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right)} \right].} \] Таким образом, криволинейный интеграл \({I_1}\) равен \[ {{I_1} = \int\limits_0^{2\pi } {\left( {2 - 2\cos 4t - 3\sin 2t + \sin 6t} \right)dt} } = {\left. {\left( {2t - \frac{{\sin 4t}}{2} + \frac{{3\cos 2t}}{2} - \frac{{\cos 6t}}{6}} \right)} \right|_0^{2\pi } } = {\left( {4\pi + \frac{3}{2} - \frac{1}{6}} \right) - \left( {\frac{3}{2} - \frac{1}{6}} \right) } = {4\pi .} \] Теперь вычислим двойной интеграл: \[ {{I_2} = \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {\frac{{\partial \left( {x{y^2}} \right)}}{{\partial x}} - \frac{{\partial \left( {{x^2}{y^2}} \right)}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {{y^2} - 2y{x^2}} \right)dxdy} .} \] В полярных координатах он равен \[ {{I_2} = \iint\limits_R {\left( {{y^2} - 2y{x^2}} \right)dxdy} } = {\int\limits_0^{2\pi } {\int\limits_0^2 {\left[ {{{\left( {r\sin \theta } \right)}^2} - 2r\sin \theta {{\left( {r\cos \theta } \right)}^2}} \right]rdrd\theta } } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^2 {\left( {{r^2}{{\sin }^2}\theta - 2{r^3}\sin \theta \,{{\cos }^2}\theta } \right)rdr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^2 {\left( {{r^3}{{\sin }^2}\theta - 2{r^4}\sin \theta \,{{\cos }^2}\theta } \right)dr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\left. {\left( {\frac{{{r^4}}}{4}{{\sin }^2}\theta - \frac{{2{r^5}}}{5}\sin \theta \,{{\cos }^2}\theta } \right)} \right|_{r = 0}^2} \right]d\theta } } = {\int\limits_0^{2\pi } {\left( {4{{\sin }^2}\theta - \frac{{64}}{5}\sin \theta \,{{\cos }^2}\theta } \right)d\theta } } = {4\int\limits_0^{2\pi } {{{\sin }^2}\theta d\theta } - \frac{{64}}{5}\int\limits_0^{2\pi } {\sin \theta \,{{\cos }^2}\theta d\theta } } = {4\int\limits_0^{2\pi } {\frac{{1 - \cos 2\theta }}{2}d\theta } } + {\frac{{64}}{5}\int\limits_0^{2\pi } {{{\cos }^2}\theta \,d\left( {\cos \theta } \right)} } = {2\left[ {\left. {\left( {\theta - \frac{{\sin 2\theta }}{2}} \right)} \right|_0^{2\pi }} \right] } + {\frac{{64}}{5}\left[ {\left. {\left( {\frac{{{{\cos }^3}\theta }}{3}} \right)} \right|_0^{2\pi }} \right] } = {4\pi .} \] Как видно, \({I_1} = {I_2}.\)