Решение дифференциальных уравнений с помощью рядов Фурье

Теория рядов Фурье первоначально была создана для решения дифференциальных уравнений. Поэтому, неудивительно, что ряды Фурье широко используются для поиска решений как обыкновенных дифференциальных уравнений, так и уравнений в частных производных.

В настоящем разделе мы расмотрим приложение рядов Фурье к решению некоторых обыкновенных дифференциальных уравнений, а также к решению трех наиболее популярных типов уравнений математической физики:

• Уравнение теплопроводности \({\large\frac{{\partial u}}{{\partial t}}\normalsize} = k\large\frac{{{\partial ^2}u}}{{\partial {x^2}}}\normalsize;\)

• Волновое уравнение \({\large\frac{{{\partial ^2}u}}{{\partial {t^2}}}\normalsize} = {a^2}\large\frac{{{\partial ^2}u}}{{\partial {x^2}}}\normalsize;\)

• Уравнение Лапласа \({\large\frac{{{\partial ^2}u}}{{\partial {x^2}}}\normalsize} + {\large\frac{{{\partial ^2}u}}{{\partial {y^2}}}\normalsize} = 0.\)

   Пример 1

Найти решение в виде ряда Фурье дифференциального уравнения \(y'' + 2y = 3x\) с граничными условиями \(y\left( 0 \right) = y\left( 1 \right) = 0.\) Мы будем использовать разложение по нечетным гармоникам для построения неоднородного решения уравнения с заданными граничными условиями. Опираясь на результаты примера \(3\) раздела Определение ряда Фурье и типичные примеры, можно записать правую часть уравнения в виде ряда \[3x = \frac{6}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin n\pi x} .\] Предположим, что решение уравнения имеет вид \[y\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin n\pi x} .\] Подставляя это в само уравнение, получаем соотношение \[ {\sum\limits_{n = 1}^\infty {\left( { - {n^2}{\pi ^2}} \right){b_n}\sin n\pi x} + 2\sum\limits_{n = 1}^\infty {{b_n}\sin n\pi x} } = {\frac{6}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin n\pi x} .} \] Поскольку коэффициенты при каждой гармонике в левой и правой части должны быть равны друг другу, получаем алгебраическое уравнение \[ {\left( {2 - {n^2}{\pi ^2}} \right){b_n} = \frac{{6{{\left( { - 1} \right)}^{n + 1}}}}{{n\pi }}}\;\; {\text{или}\;\;{b_n} = \frac{{6{{\left( { - 1} \right)}^{n + 1}}}}{{n\pi \left( {2 - {n^2}{\pi ^2}} \right)}}.} \] Следовательно, решение исходного дифференциального уравнения описывается рядом \[y\left( x \right) = \frac{6}{\pi }\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{{n\left( {2 - {n^2}{\pi ^2}} \right)}}\sin n\pi x} .\]

   Пример 2

Найти периодические решения дифференциального уравнения \(y' + ky = f\left( x \right),\) где \(k\) − константа, а \(f\left( x \right)\) − периодическая функция. Представим функцию \(f\left( x \right)\) в правой части уравнения в виде ряда Фурье в комплексной форме: \[f\left( x \right) = \sum\limits_{n = - \infty }^\infty {{c_n}{e^{inx}}} .\] Здесь комплексные коэффициенты Фурье определяются формулой \[{c_n} = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( x \right){e^{ - inx}}dx} .\] Предполагая, что решение уравнения представляется рядом Фурье \[y = \sum\limits_{n = - \infty }^\infty {{y_n}{e^{inx}}} ,\] найдем выражение для производной: \[y' = \sum\limits_{n = - \infty }^\infty {in{y_n}{e^{inx}}} .\] Подставляя это в исходное дифференциальное уравнение, получаем \[\sum\limits_{n = - \infty }^\infty {in{y_n}{e^{inx}}} + k\sum\limits_{n = - \infty }^\infty {{y_n}{e^{inx}}} = \sum\limits_{n = - \infty }^\infty {{c_n}{e^{inx}}} .\] Поскольку данное равенство справедливо при всех значениях \(n,\) то получаем следующее соотношение: \[in{y_n} + k{y_n} = {c_n}\;\;\text{или}\;\;{y_n} = \frac{{{c_n}}}{{in + k}}.\] Здесь \({c_n}\) и \(k\) − известные числа. Следовательно, решение выражается формулой \[y\left( x \right) = \sum\limits_{n = - \infty }^\infty {\frac{{{c_n}}}{{in + k}}{e^{inx}}} .\]

   Пример 3

Используя разложение в ряд Фурье, решить одномерное уравнение теплопроводности \[\frac{{\partial T}}{{\partial t}} = k\frac{{{\partial ^2}T}}{{\partial {x^2}}}\] с граничными условиями Дирихле: \(T = {T_1}\) при \(x = 0\) и \(T = {T_2}\) при \(x = L.\) Начальное распределение температуры задано функцией \(T\left( {x,0} \right) = f\left( x \right).\) Сначала мы определим стационарное распределение температуры при заданных граничных условиях.
Рассмотрим уравнение \(k\large\frac{{{\partial ^2}T}}{{\partial {x^2}}}\normalsize = 0.\) Интегрируя его, найдем общее решение: \[{T_0}\left( x \right) = {C_1} + {C_2}x.\] Коэффициенты \({C_1}\) и \({C_2}\) найдем из граничных условий: \({T_0}\left( 0 \right) = {T_1},\) \({T_0}\left( L \right) = {T_2}.\) В результате получаем \[{T_0}\left( x \right) = {T_1} + \left( {{T_2} - {T_1}} \right)\frac{x}{L}.\] Построим теперь решение задачи, зависящее от времени.
Введем новую переменную \[y\left( {x,t} \right) = T\left( {x,t} \right) - {T_0}\left( x \right).\] Граничные условия для \(y\left( {x,t} \right)\) принимают вид: \[y\left( {0,t} \right) = y\left( {L,t} \right) = 0,\] а начальное распределение записывается в форме \[y\left( {x,0} \right) = f\left( x \right) - {T_0}\left( x \right) = g\left( x \right).\] Принимая во внимание новые граничные условия, будет естественным искать решение в виде разложения по нечетным гармоникам. Тогда \[g\left( x \right) = \sum\limits_{n = 0}^\infty {{b_n}\sin \frac{{n\pi x}}{L}} ,\] где коэффициенты \({b_n}\) находятся по формуле \[{b_n} = \frac{2}{L}\int\limits_0^L {g\left( x \right)\sin \frac{{n\pi x}}{L}dx} .\] (Мы предполагаем, что эти коэффициенты известны.)

Общее решение будем искать в виде ряда с коэффициентами \({c_n}\left( t \right),\) зависящими от времени: \[y\left( {x,t} \right) = \sum\limits_{n = 0}^\infty {{c_n}\left( t \right)\sin \frac{{n\pi x}}{L}} .\] Очевидно, что граничные условия \(y\left( {0,t} \right) = 0\) и \(y\left( {L,t} \right) = 0\) выполняются при любых значениях времени \(t > 0.\) Начальные условия для \({c_n}\left( t \right)\) имеют вид \[{c_n}\left( 0 \right) = {b_n},\;\;n = 0,1,2, \ldots \] Подставим эти выражения в уравнение теплопроводности \(k\large\frac{{{\partial ^2}y}}{{\partial {x^2}}}\normalsize = \large\frac{{\partial y}}{{\partial t}}\normalsize.\) Тогда \[ - k\sum\limits_{n = 0}^\infty {\frac{{{n^2}{\pi ^2}}}{{{L^2}}}{c_n}\left( t \right)\sin \frac{{n\pi x}}{L}} = \sum\limits_{n = 0}^\infty {\frac{{d{c_n}\left( t \right)}}{{dt}}\sin \frac{{n\pi x}}{L}} .\] Умножим обе части последнего выражения на \({\sin \large\frac{{m\pi x}}{L}\normalsize}\) и проинтегрируем на интервале \(\left[ {0,L} \right],\) используя соотношения ортогональности \[ \int\limits_0^L {\sin \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}dx} = \begin{cases} 0, & \text{если} & m \ne n \\ \frac{L}{2}, & \text{если} & m = n \end{cases}. \] В результате получаем \[ {- k\sum\limits_{n = 0}^\infty {\frac{{{n^2}{\pi ^2}}}{{{L^2}}}{c_n}\left( t \right)\int\limits_0^L {\sin \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}dx} } } = {\sum\limits_{n = 0}^\infty {\frac{{d{c_n}\left( t \right)}}{{dt}}\int\limits_0^L {\sin \frac{{n\pi x}}{L}\sin \frac{{m\pi x}}{L}dx} } ,} \] или \[ - k\frac{{{m^2}{\pi ^2}}}{{{L^2}}}{c_m}\left( t \right) = \frac{{d{c_m}\left( t \right)}}{{dt}}.\] Решая полученное обыкновенное дифференциальное уравнение, находим \({{c_n}\left( t \right)}.\) \[ {\frac{{d{c_m}}}{{{c_m}}} = - \frac{{k{m^2}{\pi ^2}}}{{{L^2}}}dt,}\;\; {\Rightarrow \int {\frac{{d{c_m}}}{{{c_m}}}} = - \frac{{k{m^2}{\pi ^2}}}{{{L^2}}}\int {dt} ,}\;\; {\Rightarrow \ln {c_m}\left( t \right) = - \frac{{k{m^2}{\pi ^2}}}{{{L^2}}}t + {C_0},}\;\; {\Rightarrow {c_m}\left( t \right) = A\exp \left( { - \frac{{k{m^2}{\pi ^2}}}{{{L^2}}}t} \right).} \] Поскольку в данном случае \(m = n,\) то можно записать \[{c_n}\left( t \right) = A\exp \left( { - \frac{{k{n^2}{\pi ^2}}}{{{L^2}}}t} \right),\] где \(A = {e^{{C_0}}}\) − постоянная, зависящая от начальных условий.

Учитывая, что \({c_n}\left( 0 \right) = {b_n},\) получаем решение для \({c_n}\left( t \right)\) в форме \[{c_n}\left( t \right) = {b_n}\exp \left( { - \frac{{k{n^2}{\pi ^2}}}{{{L^2}}}t} \right).\] Следовательно, окончательное решение уравнения теплопроводности выражается формулой \[ {T\left( {x,t} \right) = {T_0}\left( x \right) + \sum\limits_{n = 0}^\infty {{b_n}\exp \left( { - \frac{{k{n^2}{\pi ^2}}}{{{L^2}}}t} \right)\sin \frac{{n\pi x}}{L}} } = {{T_1} + \left( {{T_2} - {T_1}} \right)\frac{x}{L} + \sum\limits_{n = 0}^\infty {{b_n}\exp \left( { - \frac{{k{n^2}{\pi ^2}}}{{{L^2}}}t} \right)\sin \frac{{n\pi x}}{L}} .} \]

   Пример 4

Найти решение волнового уравнения \[\frac{{{\partial ^2}u}}{{\partial {t^2}}} = {a^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}},\;\;0 \le x \le L\] для струны с закрепленными концами с граничными условиями \(u\left( {0,t} \right) = u\left( {L,t} \right) = 0.\) Начальное смещение и скорость заданы в виде \[u\left( {x,0} \right) = f\left( x \right),\;\;\frac{{\partial u\left( {x,0} \right)}}{{\partial t}} = g\left( x \right),\] где \(f\left( x \right)\) и \(g\left( x \right)\) − некоторые функции, которые считаются известными в данной задаче. При этом должны быть выполнены соотношения \[f\left( 0 \right) = f\left( L \right) = g\left( 0 \right) = g\left( L \right) = 0.\] Будем искать все периодические решения задачи, в которых разделяются переменные \(x\) и \(t,\) т.е. в форме \[u\left( {x,t} \right) = X\left( x \right) \cdot T\left( t \right).\] Тогда \[ {\frac{{{\partial ^2}u}}{{\partial {t^2}}} = XT''}\;\; {\text{и}\;\;\frac{{{\partial ^2}u}}{{\partial {x^2}}} = X''T.} \] Подставляя это в волновое уравнение, получаем \[ {XT'' = {a^2}X''T\;\;\text{или}}\;\; {\frac{{X''}}{X} = \frac{{T''}}{{{a^2}T}}.} \] В последней записи функция в левой части зависит только от \(x,\) а функция в правой части − только от \(t.\) Это возможно, если только обе части уравнения равны некоторой константе. Следовательно, \[\frac{{X''}}{X} = \frac{{T''}}{{{a^2}T}} = \text{const} = \alpha .\] Если константа \(\alpha\) положительная, то полагая \(\alpha = {\lambda ^2},\) получим уравнение \[T'' = {a^2}{\lambda ^2}T\] с общим решением \[T\left( t \right) = a\sinh \left( {a\lambda t} \right) + b\cosh \left( {a\lambda t} \right).\] Такое решение не содержит периодических функций по \(t.\) Поэтому рассмотрим вариант, когда константа \(\alpha\) отрицательна: \(\alpha = - {\lambda ^2}.\) В этом случае волновое уравнение расщепляется на два обыкновенных дифференциальных уравнения: \[X'' + {\lambda ^2}X = 0,\;\;T'' + {a^2}{\lambda ^2}T = 0.\] Решая первое уравнение, находим \[X\left( x \right) = {C_1}\cos \lambda x + {C_2}\sin\lambda x,\] где \({C_1}\) и \({C_2}\) − постоянные интегрирования.

Учитывая граничные условия, получаем \[X\left( 0 \right) = X\left( L \right) = 0.\] Тогда \[ {X\left( 0 \right) = {C_1} = 0,}\;\; {X\left( L \right) = {C_2}\sin \lambda L = 0.} \] Полагая \({C_2} \ne 0\) (в противном случае мы бы получили тривиальное решение \(X \equiv 0\)), находим, что \(\lambda L = \pi n\) (\(n\) − целое число).

Следовательно, так называемые собственные значения равны \[{\lambda _n} = \frac{{\pi n}}{L},\;\;n = 1,2,3, \ldots \] Соответствующие им собственные функции записываются в виде \[{X_n}\left( x \right) = \sin \frac{{\pi nx}}{L}.\] При \(\lambda = {\lambda _n}\) второе уравнение имеет решение \[ {{T_n} = {A_n}\cos a{\lambda _n}t + {B_n}\sin a{\lambda _n}t } = {{A_n}\cos \frac{{a\pi nt}}{L} + {B_n}\sin \frac{{a\pi nt}}{L}.} \] Таким образом, можно записать, что \[ {{u_n}\left( {x,t} \right) } = {\sin \frac{{\pi nx}}{L}\left( {{A_n}\cos \frac{{a\pi nt}}{L} + {B_n}\sin\frac{{a\pi nt}}{L}} \right).} \] Здесь \(n\) − целое число, а \({A_n}\) и \({B_n}\) − постоянные, зависящие от начальных условий.

Теперь мы можем построить общее решение волнового уравнения как линейную комбинацию частных решений: \[ {u\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {{u_n}\left( {x,t} \right)} } = {\sum\limits_{n = 1}^\infty {\sin \frac{{\pi nx}}{L}\left( {{A_n}\cos \frac{{a\pi nt}}{L} + {B_n}\sin\frac{{a\pi nt}}{L}} \right)}. } \] Предполагая, что этот ряд дифференцируемый, запишем выражение для производной: \[ {\frac{{\partial u\left( {x,t} \right)}}{{\partial t}} } = {\sum\limits_{n = 1}^\infty {\sin \frac{{\pi nx}}{L}\left( { - {A_n}\frac{{a\pi n}}{L}\sin\frac{{a\pi nt}}{L} + {B_n}\frac{{a\pi n}}{L}\cos\frac{{a\pi nt}}{L}} \right).} } \] Теперь из начальных условий определим постоянные \({A_n}\) и \({B_n}:\) \[ {u\left( {x,0} \right) = \sum\limits_{n = 1}^\infty {{A_n}\sin \frac{{\pi nx}}{L}} = f\left( x \right),}\;\; {\frac{{\partial u\left( {x,0} \right)}}{{\partial t}} = \sum\limits_{n = 1}^\infty {{B_n}\frac{{a\pi n}}{L}\sin \frac{{\pi nx}}{L}} = g\left( x \right).} \] Видно, что функции \(f\left( x \right)\) и \(g\left( x \right)\) следует разложить по ортогональной системе \(\left\{ {\sin \large\frac{{\pi nx}}{L}\normalsize} \right\}.\) По формулам для коэффициентов Фурье получаем \[ {{A_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\sin \frac{{\pi nx}}{L}dx} ,}\;\; {{B_n} = \frac{2}{{a\pi n}}\int\limits_0^L {g\left( x \right)\sin \frac{{\pi nx}}{L}dx} ,}\;\; {n = 1,2,3, \ldots } \] Таким образом, решение волнового уравнения с заданными граничными и начальными условиями имеет вид \[ {u\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {{u_n}\left( {x,t} \right)} } = {\sum\limits_{n = 1}^\infty {\sin \frac{{\pi nx}}{L}\left( {{A_n}\cos \frac{{a\pi nt}}{L} + {B_n}\sin\frac{{a\pi nt}}{L}} \right)}, } \] где коэффициенты \({A_n}\) и \({B_n}\) определяются приведенными выше формулами.

Первый член ряда \({u_1}\left( {x,t} \right)\) называется основной частотой, остальные члены \({u_n}\left( {x,t} \right)\) − обертонами или гармониками. Период и частота гармоники определяются формулами \[{T_n} = \frac{{2L}}{{an}},\;\;{\omega _n} = \frac{{a\pi n}}{L}.\]

   Пример 5

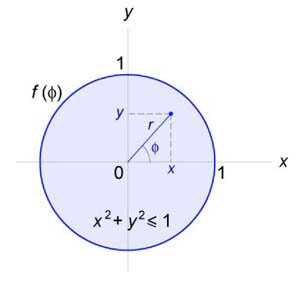
Найти решение уравнения Лапласа \[\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} = 0\] в круге \({x^2} + {y^2} \le 1\) c граничным условием \[{\left. {u\left( {x,y} \right)} \right|_{{x^2} + {y^2} = 1}} = f\left( {x,y} \right).\] Будем искать решение в полярных координатах \(\left( {r,\varphi } \right).\) Взаимосвязь между декартовыми и полярными координатами определяется стандартными формулами (рисунок \(1\)): \[x = r\cos \varphi ,\;\;y = r\sin \varphi .\] Решением задачи будет функция \(u\left( {r,\varphi } \right),\) зависящая от переменных \(r\) и \(\varphi.\) Очевидно, \(u\left( {r,\varphi } \right),\) является \(2\pi\)-периодической функцией по \(\varphi.\) При этом граничная функция \(f\left( {x,y} \right)\) преобразуется в функцию \(f\left( \varphi \right),\) зависящую только от переменной \(\varphi.\)

Уравнение Лапласа в полярных координатах записывается в виде \[{r^2}\frac{{{\partial ^2}u}}{{\partial {r^2}}} + r\frac{{\partial u}}{{\partial r}} + \frac{{{\partial ^2}u}}{{\partial {\varphi ^2}}} = 0.\] Будем искать решение \(u\left( {r,\varphi } \right)\) в виде ряда Фурье \[ {u\left( {r,\varphi } \right) } = {\frac{{{a_0}\left( r \right)}}{2} + \sum\limits_{n = 1}^\infty {\left[ {{a_n}\left( r \right)\cos n\varphi + {b_n}\left( r \right)\sin n\varphi } \right]} ,} \] где коэффициенты Фурье \({{a_n}\left( r \right)}\) и \({{b_n}\left( r \right)}\) зависят от радиуса \(r.\)

Предполагая, что функция \(u\left( {r,\varphi } \right)\) является достаточно гладкой и допускает двойное дифференцирование по \(r\) и \(\varphi,\) получаем следующие выражения для производных: \[\frac{{\partial u}}{{\partial r}} = \frac{{{a'_0} \left( r \right)}}{2} + \sum\limits_{n = 1}^\infty {\left[ {{a'_n} \left( r \right)\cos n\varphi + {b'_n} \left( r \right)\sin n\varphi } \right]} ,\] \[\frac{{{\partial ^2}u}}{{\partial {r^2}}} = \frac{{{a''_0} \left( r \right)}}{2} + \sum\limits_{n = 1}^\infty {\left[ {{a''_n}\left( r \right)\cos n\varphi + {b''_n}\left( r \right)\sin n\varphi } \right]} ,\] \[\frac{{\partial u}}{{\partial \varphi }} = \sum\limits_{n = 1}^\infty {\left[ { - {a_n}\left( r \right)n\sin n\varphi + {b_n}\left( r \right)n\cos n\varphi } \right]} ,\] \[\frac{{{\partial ^2}u}}{{\partial {\varphi ^2}}} = \sum\limits_{n = 1}^\infty {\left[ { - {a_n}\left( r \right){n^2}\cos n\varphi - {b_n}\left( r \right){n^2}\sin n\varphi } \right]} .\] Подставляя это в уравнение Лапласа, находим \[ {\frac{{{r^2}{a''_0}\left( r \right)}}{2} + \frac{{r{a'_0} \left( r \right)}}{2} } + {\sum\limits_{n = 1}^\infty {\left[ {\left( {{r^2}{a''_n}\left( r \right) + r{a'_n} \left( r \right) - {n^2}{a_n}\left( r \right)} \right)\cos n\varphi } \right.} } + {\left. {\left( {{r^2}{b''_n}\left( r \right) + r{b'_n} \left( r \right) - {n^2}{b_n}\left( r \right)} \right)\sin n\varphi } \right] = 0.} \] Поскольку это выражение равно нулю при всех \(r\) и \(\varphi,\) то приходим к выводу, что \[{r^2}{a''_n}\left( r \right) + r{a'_n} \left( r \right) - {n^2}{a_n}\left( r \right) = 0\;\;\text{для}\;\;n = 0,1,2,3, \ldots \] \[{r^2}{b''_n}\left( r \right) + r{b'_n} \left( r \right) - {n^2}{b_n}\left( r \right) = 0\;\;\text{для}\;\;n = 1,2,3, \ldots \] Таким образом, мы получили систему обыкновенных дифференциальных уравнений вместо исходного уравнения в частных производных (этот метод был предложен Жозефом Фурье в \(1822\)). Важно, что каждое уравнение в системе решается независимо.

Убедимся, что полученным уравнениям удовлетворяют функции вида \[{a_n}\left( r \right) = {a_n}\left( 1 \right){r^n},\;\;{b_n}\left( r \right) = {b_n}\left( 1 \right){r^n}.\] Здесь постоянные \({a_n}\left( 1 \right)\) и \({b_n}\left( 1 \right)\) находятся из начальных условий к полученным обыкновенным дифференциальным уравнениям. Чтобы сформулировать эти начальные условия, разложим в ряд Фурье функцию \(f\left( \varphi \right) = u\left( {1,\varphi } \right),\) определяющую граничные условия для уравнения Лапласа в полярных координатах. В результате находим \[ {f\left( \varphi \right) } = {\frac{{{\alpha _0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{\alpha _n}\cos n\varphi + {\beta _n}\sin n\varphi } \right)} } = {u\left( {1,\varphi } \right) } = {\frac{{{a_0}\left( 1 \right)}}{2} + \sum\limits_{n = 1}^\infty {\left[ {{a_n}\left( 1 \right)\cos n\varphi + {b_n}\left( 1 \right)\sin n\varphi } \right]} .} \] Приравнивая коэффициенты слева и справа при членах \({\cos n\varphi }\) и \({\sin n\varphi },\) получаем соотношения \[{a_n}\left( 1 \right) = {\alpha _n},\;\;n = 0,1,2,3, \ldots \] \[{b_n}\left( 1 \right) = {\beta_n},\;\;n = 1,2,3, \ldots \] Следовательно, система обыкновенных дифференциальных уравнений имеет решение \[{a_n}\left( r \right) = {\alpha _n}{r^n},\;\;{b_n}\left( r \right) = {\beta _n}{r^n}.\] Тогда решение уравнения Лапласа записывается в виде \[u\left( {r,\varphi } \right) = \frac{{{\alpha _0}}}{2} + \sum\limits_{n = 1}^\infty {{r^n}\left( {{\alpha _n}\cos n\varphi + {\beta _n}\sin n\varphi } \right)} ,\] где \({{\alpha _n}},\) \({{\beta_n}}\) − известные числа, зависящие от граничных условий.

Полученный ответ можно упростить. Подставим явные выражения для коэффициентов \({{\alpha _n}},\) \({{\beta_n}}:\) \[ {u\left( {r,\varphi } \right) } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( t \right)\left[ {\frac{1}{2} + \sum\limits_{n = 1}^\infty {{r^n}\left( {\cos nt\cos n\varphi + \sin nt\sin n\varphi } \right)} } \right]dt} .} \] Заметим, что \[\cos nt\cos n\varphi + \sin nt\sin n\varphi = \cos n\left( {t - \varphi } \right).\] Поэтому \[u\left( {r,\varphi } \right) = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( t \right)\left[ {1 + 2\sum\limits_{n = 1}^\infty {{r^n}\cos n\left( {t - \varphi } \right)} } \right]dt} .\] Используя формулу \(\cos x = \large\frac{{{e^{ix}} + {e^{ - ix}}}}{2}\normalsize,\) можно показать, что выражение в квадратных скобках равно сумме бесконечно убывающей геометрической прогрессии: \[ {1 + 2\sum\limits_{n = 1}^\infty {{r^n}\cos n\left( {t - \varphi } \right)} } = {\frac{{1 - {r^2}}}{{1 - 2r\cos \left( {t - \varphi } \right) + {r^2}}}.} \] Тогда решение будет определяться формулой \[u\left( {r,\varphi } \right) = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {f\left( t \right)\frac{{1 - {r^2}}}{{1 - 2r\cos \left( {t - \varphi } \right) + {r^2}}}dt} .\] Полученное выражение называется интегралом Пуассона для единичного круга.