Дифференцирование и интегрирование рядов Фурье

Пусть \(f\left( x \right)\) является \(2\pi\)-периодической кусочно непрерывной функцией, определенной на замкнутом интервале \(\left[ { - \pi ,\pi } \right].\) Для такой функции существует разложение в ряд Фурье: \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)} .\] Если производная \(f'\left( x \right)\) данной функции также кусочно непрерывна, а сама функция \(f\left( x \right)\) удовлетворяет условиям периодичности \[f\left( { - \pi } \right) = f\left( \pi \right),\;\;f'\left( { - \pi } \right) = f'\left( \pi \right),\] то разложение в ряд Фурье производной \(f'\left( x \right)\) выражается формулой \[f'\left( x \right) = \sum\limits_{n = 1}^\infty {\left( {n{b_n}\cos nx - n{a_n}\sin nx} \right)} .\] Пусть \(g\left( x \right)\) является \(2\pi\)-периодической кусочно непрерывной функцией в интервале \(\left[ { - \pi ,\pi } \right].\) Ряд Фурье такой функции можно проинтегрировать почленно на заданном интервале.

Разложение функции \(g\left( x \right)\) в ряд Фурье определяется выражением \[g\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)} .\] Рассмотрим функцию \[ {G\left( x \right) = \int\limits_0^x {g\left( t \right)dt} } \sim {\frac{{{A_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{A_n}\cos nx + {B_n}\sin nx} \right)} ,} \] где \({A_n} = - \large\frac{{{b_n}}}{n}\normalsize,\) \({B_n} = \large\frac{{{a_n}}}{n}\normalsize.\)

Полагая \(x = 0,\) мы видим, что \[ {G\left( 0 \right) = 0 = \frac{{{A_0}}}{2} + \sum\limits_{n = 1}^\infty {{A_n}} = \frac{{{A_0}}}{2} - \sum\limits_{n = 1}^\infty {\frac{{{b_n}}}{n}} \;\;\text{или}\;\;} {\frac{{{A_0}}}{2} = \sum\limits_{n = 1}^\infty {\frac{{{b_n}}}{n}} .} \] Следовательно, разложение в ряд Фурье функции \(G\left( x \right)\) имеет вид \[ {G\left( x \right) = \int\limits_0^x {g\left( t \right)dt} } = {\int\limits_0^x {\frac{{{a_0}}}{2}dx} + \sum\limits_{n = 1}^\infty {\int\limits_0^x {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)dx} } } = {\frac{{{a_0}x}}{2} + \sum\limits_{n = 1}^\infty {\frac{{{a_n}\sin nx + {b_n}\left( {1 - \cos nx} \right)}}{n}} ,} \] где ряд в правой части получен формальным почленным интегрированием ряда Фурье функции \(g\left( x \right).\)

В последнем выражении из-за интегрирования постоянной величины возникло "лишнее" слагаемое, зависящее от \(x.\) Поэтому, чтобы сохранить определенную симметрию с разложением в ряд Фурье исходной функции \(f\left( x \right),\) рассмотрим функцию \[\Phi \left( x \right) = \int\limits_0^x {g\left( t \right)dt} - \frac{{{a_0}x}}{2}.\] Ряд Фурье функции \(\Phi\left( x \right)\) будет определяться выражением \[ {\Phi \left( x \right) = \int\limits_0^x {g\left( t \right)dt} - \frac{{{a_0}x}}{2} } = {\frac{{{A_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{A_n}\cos nx + {B_n}\sin nx} \right)} ,} \] где коэффициенты Фурье связаны соотношениями \[ {\frac{{{A_0}}}{2} = \sum\limits_{n = 1}^\infty {\frac{{{b_n}}}{n}} ,}\;\; {{A_n} = - \frac{{{b_n}}}{n},}\;\; {{B_n} = \frac{{{a_n}}}{n}.} \]

   Пример 1

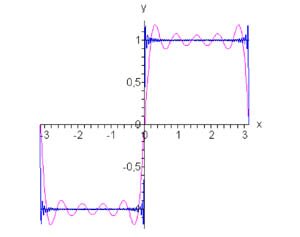
Найти ряд Фурье для функции \(\text{sign}\,x:\) \[ f\left( x \right) = \text{sign}\,x = \begin{cases} -1, & -\pi \le x \le 0 \\ 1, & 0 \lt x \le \pi \end{cases}, \] если известно, что разложение в ряд Фурье функции \(F\left( x \right) = \left| x \right|\) в интервале \(\left[ { - \pi ,\pi } \right]\) имеет вид \[F\left( x \right) = \left| x \right| = \frac{\pi }{2} - \frac{4}{\pi }\sum\limits_{n = 0}^\infty {\frac{{\cos \left( {2n + 1} \right)x}}{{{{\left( {2n + 1} \right)}^2}}}} .\] Поскольку \(f\left( x \right) = F'\left( x \right)\) для всех \(x \ne 0,\) то получаем \[f\left( x \right) = \frac{d}{{dx}}\left[ {\frac{\pi }{2} - \frac{4}{\pi }\sum\limits_{n = 0}^\infty {\frac{{\cos \left( {2n + 1} \right)x}}{{{{\left( {2n + 1} \right)}^2}}}} } \right]\] или \[f\left( x \right) = \frac{4}{\pi }\sum\limits_{n = 0}^\infty {\frac{{\sin\left( {2n + 1} \right)x}}{{2n + 1}}} .\] График данной функции и ее аппроксимации рядом Фурье показаны на рисунке \(1.\)

   Пример 2

Найти ряд Фурье функции \(f\left( x \right) = {x^2},\) зная, что \[ {x = 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx}} \;\; {\text{для}\; - \pi \le x \le \pi .} \] Так как функция \(f\left( x \right)\) кусочно непрерывна на \(\left[ { - \pi ,\pi } \right],\) то можно проинтегрировать почленно ее ряд Фурье. Получим следующее равенство: \[\int\limits_{ - \pi }^x {tdt} = 2\sum\limits_{n = 1}^\infty {\int\limits_{ - \pi }^x {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nt\,dt} } .\] Следовательно, \[ {\frac{{{x^2}}}{2} - \frac{{{\pi ^2}}}{2} = 2\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\left[ {\left. {\left( { - \frac{{\cos nt}}{{{n^2}}}} \right)} \right|_{ - \pi }^x } \right]} ,}\;\; {\Rightarrow \frac{{{x^2}}}{2} - \frac{{{\pi ^2}}}{2} = 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\left[ {\cos nx - \cos \left( { - \pi n} \right)} \right]} ,}\;\; {\Rightarrow \frac{{{x^2}}}{2} - \frac{{{\pi ^2}}}{2} = 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} - 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}{{\left( { - 1} \right)}^n}}}{{{n^2}}}} ,}\;\; {\Rightarrow \frac{{{x^2}}}{2} - \frac{{{\pi ^2}}}{2} = 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} - 2\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} .} \] В примере \(1\) на странице Неравенство Бесселя и равенство Парсеваля было показано, что \(\zeta \left( 2 \right) = \sum\limits_{n = 1}^\infty {\large\frac{1}{{{n^2}}}\normalsize} = \large\frac{{{\pi ^2}}}{6}\normalsize.\) Отсюда находим, что \[{x^2} - {\pi ^2} = 4\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} - \frac{{2{\pi ^2}}}{3}\] или \[{x^2} = \frac{{{\pi ^2}}}{3} + 4\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} .\]

   Пример 3

Найти ряд Фурье функции \(f\left( x \right) = {x^3},\) если известно, что \[ {{x^2} = \frac{{{\pi ^2}}}{3} + 4\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx}} \;\; {\text{для}\; - \pi \le x \le \pi .} \] Интегрируя почленно представленный выше ряд, получаем \[\require{cancel} {\int\limits_{ - \pi }^x {{t^2}dt} = \int\limits_{ - \pi }^x {\frac{{{\pi ^2}}}{3}dt} + 4\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^n}\int\limits_{ - \pi }^x {\frac{{\cos nt}}{{{n^2}}}dt} } ,}\;\; {\Rightarrow \left. {\left( {\frac{{{t^3}}}{3}} \right)} \right|_{ - \pi }^\pi = \left. {\left( {\frac{{{\pi ^2}}}{3}t} \right)} \right|_{ - \pi }^x + 4\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^n}\left[ {\left. {\left( {\frac{{\sin nt}}{{{n^3}}}} \right)} \right|_{ - \pi }^x} \right]} ,}\;\; {\Rightarrow \frac{{{x^3}}}{3} + \frac{{{\pi ^3}}}{3} = \frac{{{\pi ^2}}}{3}\left( {x + \pi } \right) + 4\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^n}\left[ {\frac{{\sin nx}}{{{n^3}}} - \frac{{\sin \left( { - n\pi } \right)}}{{{n^3}}}} \right]} ,}\;\; {\Rightarrow \frac{{{x^3}}}{3} + \cancel{\frac{{{\pi ^3}}}{3}} = \frac{{{\pi ^2}x}}{3} + \cancel{\frac{{{\pi ^3}}}{3}} + 4\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^n}\frac{{\sin nx}}{{{n^3}}}} ,}\;\; {\Rightarrow {x^3} = {\pi ^2}x + 12\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^3}}}\sin nx} .} \] В последнее выражение можно подставить разложение в ряд Фурье для \(x\) из примера \(3\) раздела Определение ряда Фурье и типичные примеры: \[x = 2\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{n}\sin nx} .\] Тогда окончательный ответ имеет вид \[ {{x^3} = 2{\pi ^2}\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} + 12\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^3}}}\sin nx} } = {\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^n}\left( {\frac{{12}}{{{n^3}}} - \frac{{2{\pi ^2}}}{n}} \right)\sin nx} .} \]

   Пример 4

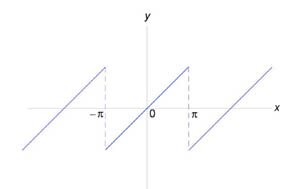
Исследовать процесс почленного дифференцирования ряда Фурье функции \(f\left( x \right) = x,\) заданной на интервале \(\left[ { - \pi ,\pi } \right].\) Запишем разложение в ряд Фурье для линейной функции: \[x = 2\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\frac{{\sin nx}}{n}} .\] В результате формального дифференцирования находим \[ {1 \sim 2\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\cos nx} } = {2\left( {\cos x - \cos 2x + \cos 3x - \ldots } \right).} \] Как видно, получено противоречие, поскольку ряд Фурье для единицы должен состоять лишь из одного постоянного слагаемого.

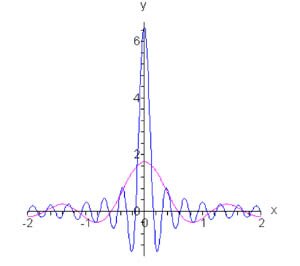
Чтобы объяснить этот парадокс, введем дельта-функцию Дирака \(\delta \left( x \right).\) Так называемое "слабое" определение \(\delta \left( x \right)\) подразумевает, что \[ \delta \left( x \right) = \begin{cases} 0, & x \ne 0 \\ \infty, & x = 0 \end{cases} \] при условии равенства единице полной площади под графиком функции: \[\int\limits_{ - \infty }^\infty {\delta \left( x \right)dx} = 1.\] Дельта-функцию можно также определить через предел при \(n \to \infty\) следующим образом: \[\delta \left( x \right) = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{2\pi }}\frac{{\sin \left( {n + \frac{1}{2}} \right)x}}{{\sin \frac{x}{2}}}.\] Графики дельта-функции при \(n = 5\) и \(n = 50\) показаны на рисунке \(2.\) Ряд Фурье для дельта-функции выражается формулой \[ {\delta \left( x \right) = \frac{1}{{2\pi }} + \frac{1}{\pi }\sum\limits_{n = 1}^\infty {\cos nx} } = {\frac{1}{{2\pi }} + \frac{1}{\pi }\sum\limits_{n = 1}^\infty {\left( {\cos x + \cos 2x + \cos 3x + \ldots } \right)} .} \] Он содержит только косинусы, поскольку дельта-функция является четной.

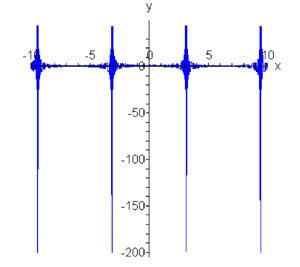
Рассмотрим теперь периодическое продолжение \({f_1}\left( x \right)\) исходной функции \(f\left( x \right)\) (рисунок \(3\)). Эта функция имеет разрывы второго рода в точках \(x = \left( {2m + 1} \right)\pi ,\;m = 0, \pm 1, \pm 2, \ldots \) Соответствующая производная \({f'_1}\left( x \right)\) содержит дельта-функцию в каждой точке разрыва, так что справедливо соотношение \[ {{f'_1}\left( x \right) = 1 - 2\pi \sum\limits_{m = - \infty }^\infty {\delta \left[ {x - \left( {2m + 1} \right)\pi } \right]} } = {1 - 2\pi \bar \delta \left( {x - \pi } \right),} \] где \(\bar \delta \left( {x - \pi } \right)\) обозначает \(2\pi\)-периодическое продолжение дельта-функции.

Отсюда видно, что \[ {\delta \left[ {x - \left( {2m + 1} \right)\pi } \right] } = {\frac{1}{{2\pi }} + \frac{1}{\pi }\sum\limits_{n = 1}^\infty {\cos n\left[ {x - \left( {2m + 1} \right)\pi } \right]} } = {\frac{1}{{2\pi }} + \frac{1}{\pi }\left\{ {\cos \left[ {x - \left( {2m + 1} \right)\pi } \right] + \cos 2\left[ {x - \left( {2m + 1} \right)\pi } \right] + \ldots } \right\} } = {\frac{1}{{2\pi }} + \frac{1}{\pi }\left\{ { - \cos x + \cos 2x - \cos 3x + \cos 4x - \ldots } \right\} } = {\frac{1}{{2\pi }} - \frac{1}{\pi }\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\cos nx} .} \] Следовательно, разложение производной \({f'_1}\left( x \right)\) в ряд имеет вид \[{f_1}^\prime \left( x \right) = 1 - 2\pi \bar \delta \left( {x - \pi } \right) = 2\sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n + 1}}\cos nx} \sim 1.\] Таким образом, функция \({f_1}^\prime \left( x \right) = 1 - 2\pi \bar \delta \left( {x - \pi } \right)\) представляет собой ряд Фурье для числа \(1.\) График этой функции приведен ниже на рисунке \(4.\)