Физические приложения тройных интегралов

Пусть тело занимает объем \(U\) и его объемная плотность в точке \(M\left( {x,y,z} \right)\) задана функцией \(\rho\left( {x,y,z} \right).\) Тогда масса тела \(m\) вычисляется с помощью тройного интеграла: \[m = \iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} .\] Статические моменты тела относительно координатных плоскостей \(Oxy, Oxz, Oyz\) выражаются формулами \[ {{M_{xy}} = \int\limits_U {z\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{M_{yz}} = \int\limits_U {x\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{M_{xz}} = \int\limits_U {y\rho \left( {x,y,z} \right)dxdydz} .} \] Координаты центра тяжести тела вычисляются по формулам: \[ {\bar x = \frac{{{M_{yz}}}}{m} = \frac{{\iiint\limits_U {x\rho \left( {x,y,z} \right)dxdydz} }}{{\iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} }},}\;\; {\bar y = \frac{{{M_{xz}}}}{m} = \frac{{\iiint\limits_U {y\rho \left( {x,y,z} \right)dxdydz} }}{{\iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} }},}\;\; {\bar z = \frac{{{M_{xy}}}}{m} = \frac{{\iiint\limits_U {z\rho \left( {x,y,z} \right)dxdydz} }}{{\iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} }}.} \] Если тело является однородным с плотностью \({\rho \left( {x,y,z} \right)} = 1\) для точек \({M\left( {x,y,z} \right)}\) в области \(U,\) то центр тяжести тела зависит только от геометрии тела и называется центроидом.

Моменты инерции тела относительно координатных плоскостей \(Oxy, Oxz, Oyz\) определяются выражениями \[ {{I_{xy}} = \iiint\limits_U {{z^2}\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{I_{yz}} = \iiint\limits_U {{x^2}\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{I_{xz}} = \iiint\limits_U {{y^2}\rho \left( {x,y,z} \right)dxdydz},} \] а моменты инерции тела относительно координатных осей \(Ox, Oy, Oz\) вычисляются по формулам \[ {{I_x} = \iiint\limits_U {\left( {{y^2} + {z^2}} \right)\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{I_y} = \iiint\limits_U {\left( {{x^2} + {z^2}} \right)\rho \left( {x,y,z} \right)dxdydz} ,}\;\; {{I_z} = \iiint\limits_U {\left( {{x^2} + {y^2}} \right)\rho \left( {x,y,z} \right)dxdydz} .} \] Как видно, справедливы соотношения \[ {{I_x} = {I_{xy}} + {I_{xz}},}\;\; {{I_y} = {I_{xy}} + {I_{yz}},}\;\; {{I_z} = {I_{xz}} + {I_{yz}}.} \] Моментом инерции тела относительно начала координат называется интеграл \[{I_0} = \iiint\limits_U {\left( {{x^2} + {y^2} + {z^2}} \right)\rho \left( {x,y,z} \right)dxdydz}.\] Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей: \[{I_0} = {I_{xy}} + {I_{yz}} + {I_{xz}}.\]
Используя рассмотренные выше \(6\) чисел \({I_x},{I_y},{I_z},{I_{xy}},{I_{xz}},{I_{yz}},\) можно составить так называемую матрицу инерции или тензор инерции тела: \[I = \left( {\begin{array}{*{20}{c}} {{I_x}}&{ - {I_{xy}}}&{ - {I_{xz}}}\\ { - {I_{xy}}}&{{I_y}}&{ - {I_{yz}}}\\ { - {I_{xz}}}&{ - {I_{yz}}}&{{I_z}} \end{array}} \right).\] Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей \(Ox', Oy', Oz'.\) Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции, а указанные направления − собственными векторами или главными осями инерции.

Если тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.

Ньютоновым потенциалом тела в точке \(P\left( {x,y,z} \right)\) называется интеграл \[u\left( {x,y,z} \right) = \iiint\limits_U {\rho \left( {\xi ,\eta ,\zeta } \right)\frac{{d\xi d\eta d\zeta }}{r}} ,\] где \({\rho \left( {\xi ,\eta ,\zeta } \right)}\) − плотность тела, и \(r = \sqrt {{{\left( {\xi - x} \right)}^2} + {{\left( {\eta - y} \right)}^2} + {{\left( {\zeta - z} \right)}^2}} .\)

Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы \(m\) и заданного распределенного тела с плотностью \({\rho \left( {\xi ,\eta ,\zeta } \right)}\) по формуле \[\mathbf{F} = - Gm\,\mathbf{\text{grad}}\,u,\] где \(G\) − гравитационная постоянная.

   Пример 1

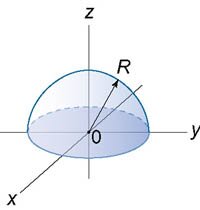
Найти центроид однородного полушара радиусом \(R.\) Введем систему координат таким образом, чтобы полушар был расположен при \(z \ge 0\) и имел центр в начале координат (рисунок \(1\)). В данной системе координат будем искать координаты центроида (центра тяжести) тела.

Очевидно, что в силу симметрии \[\bar x = \bar y = 0.\] Вычислим координату центра тяжести \(\bar z\) по формуле \[ {\bar z = \frac{{{M_{xy}}}}{m} } = {\frac{{\iiint\limits_U {z\rho \left( {x,y,z} \right)dxdydz} }}{{\iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} }}.} \] Поскольку полушар однородный, то полагаем \(\rho \left( {x,y,z} \right) = {\rho _0}.\) Тогда \[\require{cancel} {\bar z = \frac{{{\bcancel{\rho _0}}\iiint\limits_U {zdxdydz} }}{{{\bcancel{\rho _0}}\iiint\limits_U {dxdydz} }} } = {\frac{{\iiint\limits_U {zdxdydz} }}{{\iiint\limits_U {dxdydz} }} } = {\frac{{\iiint\limits_U {zdxdydz} }}{V}.} \] В знаменателе через \(V\) обозначен объем полушара, равный \[V = \frac{1}{2}\left( {\frac{4}{3}\pi {R^3}} \right) = \frac{2}{3}\pi {R^3}.\] Остается вычислить тройной интеграл \({\iiint\limits_U {zdxdydz} }.\) Для этого перейдем к сферическим координатам. При этом радиальную координату будем обозначать через \(r\) − чтобы не путать с плотностью \(\rho.\) Получаем: \[ {\iiint\limits_U {zdxdydz} } = {\iiint\limits_{U'} {r\cos \theta {r^2}\sin \theta drd\varphi d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos \theta \sin \theta d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin \theta d\left( {\sin \theta } \right)} } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot \left[ {\left. {\left( {\frac{{{{\sin }^2}\theta }}{2}} \right)} \right|_{\theta = 0}^{\theta = \large\frac{\pi }{2}\normalsize}} \right] } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot \frac{1}{2} = \frac{1}{2}\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^R} \right] } = {\frac{{{R^4}}}{8}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{{R^4}}}{8} \cdot 2\pi } = {\frac{{\pi {R^4}}}{4}.} \] Таким образом, координата центра тяжести \(\bar z\) равна \[ {\bar z = \frac{{\iiint\limits_U {zdxdydz} }}{V} } = {\frac{{\frac{1}{4}\pi {R^4}}}{{\frac{2}{4}\pi {R^3}}} = \frac{{3R}}{8}.} \]

   Пример 2

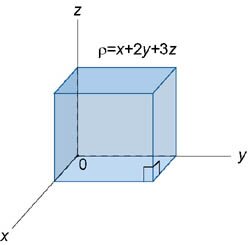
Определить массу и координаты центра тяжести единичного куба с плотностью \(\rho \left( {x,y,z} \right) = x + 2y + 3z\) (рисунок \(2\)). Сначала вычислим массу куба: \[ {m = \iiint\limits_U {\rho \left( {x,y,z} \right)dxdydz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {\left( {x + 2y + 3z} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \cdot \left[ {\left. {\left( {xz + 2yz + \frac{{3{z^2}}}{2}} \right)} \right|_{z = 0}^{z = 1}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^1 {\left( {x + 2y + \frac{3}{2}} \right)dy} } = {\int\limits_0^1 {dx} \cdot \left[ {\left. {\left( {xy + {y^2} + \frac{3}{2}y} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\int\limits_0^1 {\left( {x + 1 + \frac{3}{2}} \right)dx} } = {\int\limits_0^1 {\left( {x + \frac{5}{2}} \right)dx} } = {\left. {\left( {\frac{{{x^2}}}{2} + \frac{5}{2}x} \right)} \right|_0^1 } = {\frac{1}{2} + \frac{5}{2} = 3.} \] Теперь вычислим статические моменты \({M_{xy}},{M_{xz}},{M_{yz}}.\) \[ {{M_{xy}} = \iiint\limits_U {z\rho \left( {x,y,z} \right)dxdydz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {z\left( {x + 2y + 3z} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {\left( {xz + 2zy + 3{z^2}} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \cdot \left[ {\left. {\left( {\left( {x + 2y} \right)\frac{{{z^2}}}{2} + {z^3}} \right)} \right|_{z = 0}^{z = 1}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^1 {\left( {\frac{1}{2}\left( {x + 2y} \right) + 1} \right)dy} } = {\frac{1}{2}\int\limits_0^1 {dx} \int\limits_0^1 {\left( {x + 2y + 2} \right)dy} } = {\frac{1}{2}\int\limits_0^1 {dx} \cdot \left[ {\left. {\left( {xy + {y^2} + 2y} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\frac{1}{2}\int\limits_0^1 {\left( {x + 3} \right)dx} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{{x^2}}}{2} + 3x} \right)} \right|_0^1} \right] } = {\frac{1}{2}\left( {\frac{1}{2} + 3} \right) } = {\frac{7}{4}.} \] Аналогично находим моменты \({M_{xz}}\) и \({M_{yz}}:\) \[ {{M_{xz}} = \iiint\limits_U {y\rho \left( {x,y,z} \right)dxdydz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {y\left( {x + 2y + 3z} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {\left( {yx + 2{y^2} + 3yz} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \cdot \left[ {\left. {\left( {yxz + 2{y^2}z + \frac{{3y{z^2}}}{2}} \right)} \right|_{z = 0}^{z = 1}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^1 {\left( {yx + 2{y^2} + \frac{{3y}}{2}} \right)dy} } = {\int\limits_0^1 {dx} \cdot \left[ {\left. {\left( {\frac{{x{y^2}}}{2} + \frac{{2{y^3}}}{3} + \frac{{3{y^2}}}{4}} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\int\limits_0^1 {\left( {\frac{x}{2} + \frac{2}{3} + \frac{3}{4}} \right)dx} } = {\int\limits_0^1 {\left( {\frac{x}{2} + \frac{{17}}{{12}}} \right)dx} } = {\left. {\left( {\frac{{{x^2}}}{4} + \frac{{17x}}{{12}}} \right)} \right|_0^1 } = {\frac{1}{4} + \frac{{17}}{{12}} } = {\frac{{20}}{{12}} = \frac{5}{3}.} \] \[ {{M_{yz}} = \iiint\limits_U {x\rho \left( {x,y,z} \right)dxdydz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {x\left( {x + 2y + 3z} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \int\limits_0^1 {\left( {{x^2} + 2xy + 3xz} \right)dz} } = {\int\limits_0^1 {dx} \int\limits_0^1 {dy} \cdot \left[ {\left. {\left( {{x^2}z + 2xyz + \frac{{3x{z^2}}}{2}} \right)} \right|_{z = 0}^{z = 1}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^1 {\left( {{x^2} + 2xy + \frac{{3x}}{2}} \right)dy} } = {\int\limits_0^1 {dx} \cdot \left[ {\left. {\left( {{x^2}y + x{y^2} + \frac{{3xy}}{2}} \right)} \right|_{y = 0}^{y = 1}} \right] } = {\int\limits_0^1 {\left( {{x^2} + x + \frac{{3x}}{2}} \right)dx} } = {\int\limits_0^1 {\left( {{x^2} + \frac{{5x}}{2}} \right)dx} } = {\left. {\left( {\frac{{{x^3}}}{3} + \frac{{5{x^2}}}{4}} \right)} \right|_0^1 } = {\frac{1}{3} + \frac{5}{4} = \frac{{19}}{{12}}.} \] Вычисляем координаты центра тяжести куба: \[ {\bar x = \frac{{{M_{yz}}}}{m} = \frac{{\frac{{19}}{{12}}}}{3} = \frac{{19}}{{36}},}\;\;\; {\bar y = \frac{{{M_{xz}}}}{m} = \frac{{\frac{5}{3}}}{3} = \frac{5}{9} = \frac{{20}}{{36}},}\;\;\; {\bar z = \frac{{{M_{xy}}}}{m} = \frac{{\frac{7}{4}}}{3} = \frac{7}{{12}} = \frac{{21}}{{36}}.} \]

   Пример 3

Найти массу шара радиуса \(R,\) плотность \(\gamma\) которого пропорциональна квадрату расстояния от центра. По условию, плотность \(\gamma\) задана соотношением \(\gamma = a{r^2},\) где \(a\) − некоторая постоянная, \(r\) − расстояние от центра. Массу шара удобно вычислить в сферических координатах: \[ {m = \iiint\limits_U {\gamma \left( {r,\varphi ,\theta } \right){r^2}\sin \theta drd\varphi d\theta } } = {\iiint\limits_U {a{r^2}{r^2}\sin \theta drd\varphi d\theta } } = {a\iiint\limits_U {{r^4}\sin \theta drd\varphi d\theta } } = {a\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^4}dr} \int\limits_0^\pi {\sin \theta d\theta } } = {a\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^4}dr} \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] } = {a\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^4}dr} \cdot \left( { - \cos \pi + \cos 0} \right) } = {2a\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^4}dr} } = {2a\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{r^5}}}{5}} \right)} \right|_0^R} \right] } = {\frac{{2a{R^5}}}{5}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{2a{R^5}}}{5} \cdot 2\pi } = {\frac{{4a\pi {R^5}}}{5}.} \]

   Пример 4

Найти момент инерции прямого круглого однородного конуса относительно его оси. Конус имеет радиус основания \(R,\) высоту \(H\) и общую массу \(m\) (рисунок \(3\)). Момент инерции тела относительно оси \(Oz\) выражается формулой \[{I_z} = \iiint\limits_U {\gamma \left( {x,y,z} \right)\left( {{x^2} + {y^2}} \right)dxdydz} .\] Поскольку конус является однородным, то плотность \(\gamma \left( {x,y,z} \right) = {\gamma _0}\) можно вынести за знак интеграла: \[{I_z} = {\gamma _0}\int\limits_U {\left( {{x^2} + {y^2}} \right)dxdydz} .\] Перейдем к цилиндрическим координатам с помощью замены \[ {x = r\cos \varphi ,}\;\; {y = r\sin \varphi ,}\;\; {\Rightarrow {x^2} + {y^2} = {r^2},}\;\; {dxdydz = rdrd\varphi dz.} \] Новые переменные изменяются в пределах \[ {0 \le r \le R,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {r\frac{H}{R} \le z \le H.} \] Тогда момент инерции равен \[ {{I_z} = {\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \int\limits_{r\frac{H}{R}}^H {dz} } = {{\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}dr} \cdot \left[ {\left. z \right|_{r\frac{H}{R}}^H} \right] } = {{\gamma _0}\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {{r^3}\left( {H - r\frac{H}{R}} \right)dr} } = {{\gamma _0}H\int\limits_0^{2\pi } {d\varphi } \int\limits_0^R {\left( {{r^3} - \frac{{{r^4}}}{R}} \right)dr} } = {{\gamma _0}H\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4} - \frac{{{r^5}}}{{5R}}} \right)} \right|_0^R} \right] } = {{\gamma _0}H\int\limits_0^{2\pi } {\left( {\frac{{{R^4}}}{4} - \frac{{{R^4}}}{5}} \right)d\varphi } } = {\frac{{{\gamma _0}H{R^4}}}{{20}}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{{\gamma _0}H{R^4}}}{{20}} \cdot 2\pi } = {\frac{{{\gamma _0}\pi H{R^4}}}{{10}}.} \] Выразим плотность \({\gamma _0}\) через известную массу конуса \(m.\) Так как \[ {m = {\gamma _0}V,}\;\; {V = \frac{1}{3}\pi {R^2}H,} \] то, следовательно \[ {{\gamma _0} = \frac{m}{V} } = {\frac{m}{{\frac{1}{3}\pi {R^2}H}} } = {\frac{{3m}}{{\pi {R^2}H}}.} \] Окончательно получаем \[ {{I_z} = \frac{{{\gamma _0}\pi H{R^4}}}{{10}} } = {\frac{{3m}}{{\bcancel{\pi} {R^2}\bcancel{H}}} \cdot \frac{{\bcancel{\pi} \bcancel{H}{R^4}}}{{10}} } = {\frac{{3m{R^2}}}{{10}}.} \] Интересно, что момент инерции конуса не зависит от его высоты.

   Пример 5

С какой силой притягивает однородный шар массы \(M\) материальную точку массы \(m\), расположенную на расстоянии \(a\) от центра шара \(\left( {a > R} \right)?\) Без снижения общности материальную точку можно поместить на оси \(Oz\) (рисунок \(4\)), так что ее координата составляет \(\left( {0,0,a} \right).\) Решим задачу следующим образом. Сначала вычислим потенциал шара, а затем найдем силу притяжения материальной точки и шара. При этом для нахождения потенциала шара вместо вычисления тройного интеграла технически удобно сначала определить потенциал сферы (через поверхностный интеграл), а затем уже получить результат для шара (выполнив еще одно интегрирование).

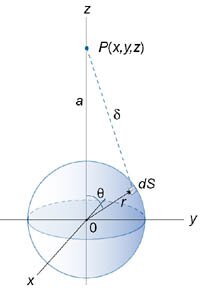
Итак, вычислим потенциал сферы произвольного радиуса \(r\) \(\left( {r \le R} \right).\) Выделим на сфере малый участок площадью \(dS,\) как показано на рисунке \(5.\) Масса этого участка равна \[dM = \rho \left( r \right)drdS,\] где \(\rho \left( r \right)\) − плотность сферы, а \(d\) − ее толщина. Указанная сфера создает в точке \(P\) потенциал, равный \[ {du = \rho \left( r \right)dr\iint\limits_S {\frac{{dS}}{\delta }} } = {\rho \left( r \right)dr\iint\limits_S {\frac{{dS}}{{\sqrt {{a^2} + {r^2} - 2ar\cos \theta } }}} ,} \] где расстояние \(\delta\) от участка \(dS\) до точки \(P\) выражено по теореме косинусов через величины \(a, r, \theta.\)

Учитывая, что элемент площади равен \(dS = {r^2}\sin \theta d\theta d\varphi,\) получаем \[ {du = \rho \left( r \right)dr\int\limits_S {\frac{{dS}}{{\sqrt {{a^2} + {r^2} - 2ar\cos \theta } }}} } = {\rho \left( r \right)dr\int\limits_0^{2\pi } {d\varphi } \int\limits_0^\pi {\frac{{{r^2}\sin \theta d\theta }}{{\sqrt {{a^2} + {r^2} - 2ar\cos \theta } }}} } = {\rho \left( r \right)dr \cdot 2\pi {r^2}\int\limits_0^\pi {\frac{{\sin \theta d\theta }}{{\sqrt {{a^2} + {r^2} - 2ar\cos \theta } }}} .} \] Вычислим отдельно интеграл по переменной \(\theta.\) Сделаем следующую замену: пусть \[v = {a^2} + {r^2} - 2ar\cos \theta .\] Тогда \[ {dv = 2ar\sin \theta d\theta ,}\;\; {\Rightarrow \sin \theta d\theta = \frac{{dv}}{{2ar}}.} \] В результате находим интеграл \[ {I = \int {\frac{{\sin \theta d\theta }}{{\sqrt {{a^2} + {r^2} - 2ar\cos \theta } }}} } = {\int {\frac{{dv}}{{2ar\sqrt v }}} = \frac{1}{{ar}}\int {\frac{{dv}}{{2\sqrt v }}} } = {\frac{{\sqrt v }}{{ar}} } = {\frac{1}{{ar}}\sqrt {{a^2} + {r^2} - 2ar\cos \theta } .} \] Таким образом, потенциал сферы радиуса \(r\) равен \[ {du = \rho \left( r \right)dr \cdot 2\pi {r^2} \cdot \frac{1}{{ar}}\left[ {\left. {\left( {\sqrt {{a^2} + {r^2} - 2ar\cos \theta } } \right)} \right|_{\theta = 0}^{\theta = \pi }} \right] } = {\frac{{2\pi r\rho \left( r \right)dr}}{a}\left[ {\sqrt {{a^2} + {r^2} + 2ar} - \sqrt {{a^2} + {r^2} - 2ar} } \right] } = {\frac{{2\pi r\rho \left( r \right)dr}}{a}\left[ {\sqrt {{{\left( {a + r} \right)}^2}} - \sqrt {{{\left( {a - r} \right)}^2}} } \right] } = {\frac{{2\pi r\rho \left( r \right)dr}}{a} \cdot 2r } = {\frac{{4\pi {r^2}\rho \left( r \right)dr}}{a}.} \] Теперь можно вычислить потенциал шара радиуса \(R.\) Пусть для простоты плотность шара постоянна и равна \({\rho_0}.\) Получаем \[ {u = \int\limits_0^R {du} } = {\int\limits_0^R {\frac{{4\pi {r^2}{\rho _0}dr}}{a}} } = {\frac{{4\pi {\rho _0}}}{a}\int\limits_0^R {{r^2}dr} } = {\frac{{4\pi {\rho _0}}}{a}\left[ {\left. {\left( {\frac{{{r^3}}}{3}} \right)} \right|_0^R} \right] } = {\frac{{4\pi {\rho _0}{R^3}}}{{3a}}.} \] В полученном выражении \({\large\frac{4}{3}\normalsize} \pi {R^3} = V\) − это объем шара, а \({\rho_0}V =M\) − масса шара. В итоге мы доказали, что потенциал гравитационного поля, создаваемого шаром на расстоянии \(a\) от центра шара \(\left( {a > R} \right),\) выражается формулой \[u = \frac{M}{a}.\] Далее легко найти силу притяжения шара и материальной точки. Поскольку \[\mathbf{F} = - Gm\,\mathbf{\text{grad}}\,u,\] то сила численно равна \[ {F = Gm\frac{{\partial u}}{{\partial z}} } = {Gm{\left. {\left[ {\frac{\partial }{{\partial z}}\left( {\frac{M}{z}} \right)} \right]} \right|_{z = a}} } = { - G\frac{{mM}}{{{a^2}}}.} \] Знак "минус" означает, что сила направлена в сторону, противоположную оси \(Oz,\) т.е. является силой притяжения.

Как видно, сила притяжения шара и точки имеет такой же вид, как и сила притяжения двух точечных масс! Это один из фундаментальных результатов в астрофизике и небесной механике. Благодаря этому, планеты и звезды часто можно рассматривать как материальные точки при описании их движения. Чтобы получить этот результат, Исаак Ньютон был вынужден даже отложить публикацию своих знаменитых "Начал Философии". Возможно трудности были связаны с тем, что он не использовал сферические координаты при решении этой задачи...

   Пример 6

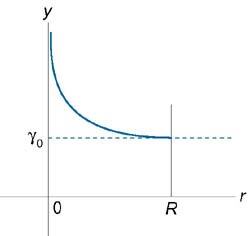
Пусть планета имеет радиус \(R,\) а ее плотность выражается зависимостью \[\gamma \left( r \right) = \frac{{R + r}}{{2r}}{\gamma _0}.\] Вычислить массу планеты. Расссмотрим подробнее закон изменения плотности. Если \(r = R,\) то \[\gamma \left( R \right) = \frac{{R + R}}{{2R}}{\gamma _0} = {\gamma _0},\] где \({\gamma_0}\) − некоторая поверхностная плотность планеты. Если \(r \to 0,\) то \(\gamma \to \infty\) (рисунок \(6\)). Массу планеты вычислим с помощью тройного интеграла по формуле: \[M = \iiint\limits_U {dV} .\] Переходя к сферическим координатам, получаем \[ {M = \iiint\limits_U {dV} } = {\iiint\limits_U {\gamma \left( r \right){r^2}\sin \theta drd\varphi d\theta } } = {\iiint\limits_U {\frac{{R + r}}{{2r}}{\gamma _0}{r^2}\sin \theta drd\varphi d\theta } } = {\frac{{{\gamma _0}}}{2}\int\limits_U {\left( {R + r} \right)r\sin \theta drd\varphi d\theta } } = {\frac{{{\gamma _0}}}{2}\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits_0^{2\pi } {d\varphi } \int\limits_0^\pi {\sin \theta d\theta } } = {\frac{{{\gamma _0}}}{2}\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] } = {\frac{{{\gamma _0}}}{2}\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits_0^{2\pi } {d\varphi } \cdot \left( { - \cos \pi + \cos 0} \right) } = {{\gamma _0}\int\limits_0^R {\left( {R + r} \right)rdr} \int\limits_0^{2\pi } {d\varphi } } = {{\gamma _0}\int\limits_0^R {\left( {R + r} \right)rdr} \cdot 2\pi } = {2\pi {\gamma _0}\int\limits_0^R {\left( {Rr + {r^2}} \right)dr} } = {2\pi {\gamma _0}\left[ {\left. {\left( {\frac{{R{r^2}}}{2} + \frac{{{r^3}}}{3}} \right)} \right|_0^R} \right] } = {2\pi {\gamma _0}\left( {\frac{{{R^3}}}{2} + \frac{{{R^3}}}{3}} \right) } = {2\pi {\gamma _0}\frac{{5{R^3}}}{6} } = {\frac{{5\pi {\gamma _0}{R^3}}}{3}.} \] Поскольку объем планеты равен \(\large\frac{4}{3}\normalsize \pi {R^3},\) то ответ можно записать и в такой форме: \[M = \frac{{5\pi {\gamma _0}{R^3}}}{3} = \frac{5}{4}{\gamma _0}V.\] Как видно, масса планеты на \(25\%\) больше по сравнению со случаем, когда плотность распределена однородно.