|
Физические задачи на оптимизацию
|
||||||
|
При исследовании физических систем часто возникает вопрос об оптимальной конфигурации, оптимальном режиме работы или экстремальных значениях величин, характеризующих систему. Такой анализ можно выполнить с помощью производной. Некоторые физические задачи на данную тему рассматриваются ниже.
|
||||||
|
Пример 1
|
||||||
|
При каком внутреннем сопротивлении источника мощность, выделяющаяся на нагрузке, будет максимальна (рисунок \(1\))?
Решение. |
||||||
|
Пример 2
|
||||||
|
Простейшая электрическая цепь состоит из источника тока с внутренним сопротивлением \(r\) и внешней нагрузки сопротивлением \(R\) (рисунок \(1\)). При каком условии коэффициент полезного действия источника будет наибольшим?
Решение.
|
||||||
|
Пример 3
|
||||||
|
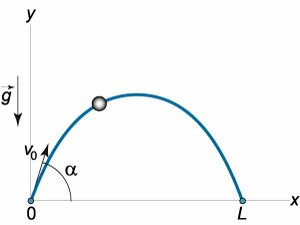
Тело брошено под углом \(\alpha\) к горизонту. Пренебрегая сопротивлением воздуха, определить угол \(\alpha,\) при котором дальность полета тела будет наибольшей.
Решение. Таким образом, максимальная дальность броска достигается при бросании тела под углом \(\alpha = \large\frac{\pi }{4}\normalsize = 45^\circ.\) Данное значение не зависит от начальной скорости \({v_0}.\) Сама же максимальная дальность \({L_{\max }}\) зависит от \({v_0}\) и определяется формулой \[ {{L_{\max }} = L\left( {\frac{\pi }{4}} \right) } = {\frac{{v_0^2}}{g}\sin\frac{\pi }{2} = \frac{{v_0^2}}{g}.} \] |
||||||
|
Пример 4
|
||||||
|
Дождевая капля с начальной массой \({m_0}\) падает под действием силы тяжести. По мере падения капля испаряется, так, что ее масса уменьшается со временем по линейному закону \(m\left( t \right) = {m_0} - bt,\) где \(b\) − скорость испарения. Определить момент времени, при котором кинетическая энергия капли будет наибольшей.
Решение. В этот момент кинетическая энергия будет равна \[ {{K_{\max }} } = {\frac{{{m_0}{g^2}{{\left( {\frac{{2{m_0}}}{{3b}}} \right)}^2}}}{2} - \frac{{b{g^2}{{\left( {\frac{{2{m_0}}}{{3b}}} \right)}^3}}}{2} } = {\frac{1}{2}\left( {\frac{{4m_0^3{g^2}}}{{9{b^2}}} - \frac{{8m_0^3{g^2}}}{{27{b^2}}}} \right) } = {\frac{1}{2} \cdot \frac{{4m_0^3{g^2}}}{{27{b^2}}} } = {\frac{{2m_0^3{g^2}}}{{27{b^2}}}.} \] |
||||||
|
Пример 5
|
||||||
|
На какой высоте над центром круглого стола надо подвесить лампочку, чтобы освещенность края была наибольшей?
Решение.
|
||||||
|
Пример 6
|
||||||
|
Груз лежит на горизонтальной поверхности. Коэффициент трения груза равен \(k.\) Определить угол \(\alpha,\) при котором сила, действующая на груз и вызывающая его перемещение, будет наименьшей.
Решение. Уравнение движения груза в векторной форме записывается в следующем виде: \[\mathbf{ma} = \mathbf{F} + \mathbf{mg} + \mathbf{F_\text{тр}} + \mathbf{N},\] В предельном случае (когда груз еще находится в покое), все силы уравновешены. Следовательно, \[\mathbf{F} + \mathbf{mg} + \mathbf{F_\text{тр}} + \mathbf{N} = \mathbf{0}.\] В проекции на координатные оси получаем следующую систему уравнений: \[\left\{ \begin{array}{l} F\cos \alpha - {F_\text{тр}} = 0\\ F\sin \alpha - mg + N = 0 \end{array} \right..\] Учтем далее, что сила трения по абсолютной величине равна \({F_\text{тр}} = kN.\) Тогда \[\left\{ \begin{array}{l} F\cos \alpha - kN = 0\\ F\sin \alpha - mg + N = 0 \end{array} \right..\] Из этой системы выразим силу \(F\) через угол \(\alpha\) и другие величины. Из второго уравнения системы следует, что \[N = mg - F\sin \alpha .\] Подставляя это в первое уравнение, находим функцию \(F\left( \alpha \right):\) \[ {F\cos \alpha - k\left( {mg - F\sin \alpha } \right) = 0,}\;\; {\Rightarrow F\cos \alpha + kF\sin \alpha - kmg = 0,}\;\; {\Rightarrow F\left( {\cos \alpha + k\sin \alpha } \right) - kmg = 0,}\;\; {\Rightarrow F = F\left( \alpha \right) = \frac{{kmg}}{{\cos \alpha + k\sin \alpha }}.} \] Продифференцируем полученное выражение по углу \(\alpha:\) \[ {F'\left( \alpha \right) } = {{\left( {\frac{{kmg}}{{\cos \alpha + k\sin \alpha }}} \right)^\prime } } = { - \frac{{kmg}}{{{{\left( {\cos \alpha + k\sin \alpha } \right)}^2}}} \cdot {\left( {\cos \alpha + k\sin \alpha } \right)^\prime } } = { - \frac{{kmg}}{{{{\left( {\cos \alpha + k\sin \alpha } \right)}^2}}} \cdot \left( { - \sin\alpha + k\cos \alpha } \right) } = {\frac{{kmg\left( {\sin\alpha - k\cos \alpha } \right)}}{{{{\left( {\cos \alpha + k\sin \alpha } \right)}^2}}}.} \] Видно, что производная равна нулю при условии \[ {\sin\alpha - k\cos \alpha = 0,}\;\; {\Rightarrow \tan\alpha - k = 0,}\;\; {\Rightarrow \tan\alpha = k,}\;\; {\Rightarrow \alpha = \arctan k.} \] Таким образом, критический угол составляет \(\alpha = \arctan k.\) Функция \(\tan \alpha\) является возрастающей при увеличении \(\alpha.\) Поэтому при переходе через данное критическое значение производная меняет знак с минуса на плюс, т.е. здесь существует минимум функции \(F\left( \alpha \right).\) Следовательно, при указанном угле \(\alpha\) сила \(F\) будет наименьшей. Вычислим значение наименьшей силы. Подставляя значение найденного угла \(\alpha,\) получаем: \[{F_{\min }} = \frac{{kmg}}{{\cos \left( {\arctan k} \right) + k\sin \left( {\arctan k} \right)}}.\] Преобразуем тригонометрические функции в знаменателе: \[ {\cos \left( {\arctan k} \right) } = {\frac{1}{{\sqrt {1 + {{\tan }^2}\left( {\arctan k} \right)} }} } = {\frac{1}{{\sqrt {1 + {k^2}} }},} \] \[ {\sin\left( {\arctan k} \right) } = {\frac{{\tan \left( {\arctan k} \right)}}{{\sqrt {1 + {{\tan }^2}\left( {\arctan k} \right)} }} } = {\frac{k}{{\sqrt {1 + {k^2}} }}.} \] В результате получаем: \[ {{F_{\min }} = \frac{{kmg}}{{\frac{1}{{\sqrt {1 + {k^2}} }} + k \cdot \frac{k}{{\sqrt {1 + {k^2}} }}}} } = {\frac{{kmg\sqrt {1 + {k^2}} }}{{1 + {k^2}}} } = {\frac{{kmg}}{{\sqrt {1 + {k^2}} }}.} \] |
||||||
|
Пример 7
|
||||||
|
Источник света расположен на прямой, соединяющей центры шаров с радиусами \({R_1}\) и \({R_2}.\) Определить положение источника, при котором площадь освещенной поверхности двух шаров является наибольшей.
Решение. Учитывая подобие прямоугольных треугольников \({AL{O_1}}\) и \({{O_1}AI},\) можно записать, что \[ {{h_1} = {R_1} - {R_1}\sin {\alpha _1},}\;\; {\text{где}\;\;\sin {\alpha _1} = \frac{{{R_1}}}{x}.} \] Следовательно, \[{h_1} = {R_1} - {R_1} \cdot \frac{{{R_1}}}{x} = {R_1} - \frac{{R_1^2}}{x}.\] Аналогичное выражение для второго шара имеет следующий вид: \[{h_2} = {R_2} - \frac{{R_2^2}}{{L - x}}.\] В таком случае суммарная освещенная площадь равна \[ {S = S\left( x \right) } = {2\pi {R_1}\left( {{R_1} - \frac{{R_1^2}}{x}} \right) + 2\pi {R_2}\left( {{R_2} - \frac{{R_2^2}}{{L - x}}} \right) } = {2\pi R_1^2 - \frac{{2\pi R_1^3}}{x} + 2\pi R_2^2 - \frac{{2\pi R_2^3}}{{L - x}}.} \] Находим производную: \[ {S'\left( x \right) } = {{\left( {2\pi R_1^2 - \frac{{2\pi R_1^3}}{x} + 2\pi R_2^2 - \frac{{2\pi R_2^3}}{{L - x}}} \right)^\prime } } = {\frac{{2\pi R_1^3}}{{{x^2}}} - \frac{{2\pi R_2^3}}{{{{\left( {L - x} \right)}^2}}}.} \] Приравнивая производную нулю, получаем следующее решение: \[ {S'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{2\pi R_1^3}}{{{x^2}}} - \frac{{2\pi R_2^3}}{{{{\left( {L - x} \right)}^2}}} = 0,}\;\; {\Rightarrow \frac{{{x^2}}}{{{{\left( {L - x} \right)}^2}}} = \frac{{R_1^3}}{{R_2^3}}.} \] При переходе через ноль производная меняет знак с плюса на минус, т.е. найденная точка является точкой максимума функции \(S\left( x \right).\) Итак, освещенная площадь будет наибольшей, когда источник находится в точке, в которой отношение квадратов расстояний от источника до центров шаров равно отношению кубов их радиусов.
|
||||||
|
Пример 8
|
||||||
|
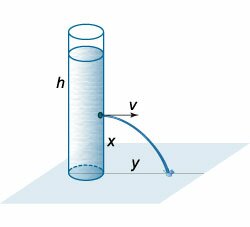
Сосуд с жидкостью высотой \(h\) расположен на горизонтальной поверхности. Сосуд имеет боковое отверстие, из которого вытекает струя. При каком положении отверстия дальность струи будет наибольшей?
Решение. Вычислим дальность струи \(y,\) предполагая, что движение жидкости описывается такими же уравнениями, как и движение материальной точки. В таком случае время, за которое жидкость, вытекающая из отверстия, достигает поверхности, равно \[t = \sqrt {\frac{{2x}}{g}} ,\] а дальность струи составляет \[y = vt = v\sqrt {\frac{{2x}}{g}} .\] Подставим сюда выражение для скорости \(v\) из формулы Торричелли: \[ {y = y\left( x \right) } = {\sqrt {2g\left( {h - x} \right)} \sqrt {\frac{{2x}}{g}} } = {2\sqrt {\frac{{\cancel{g}x\left( {h - x} \right)}}{\cancel{g}}} } = {2\sqrt {hx - {x^2}} .} \] Мы получили выражение для дальности струи \(y\) в зависимости от высоты отверстия \(x.\) Исследуем эту функцию на экстремум: \[ {y'\left( x \right) = {\left( {2\sqrt {hx - {x^2}} } \right)^\prime } } = {2 \cdot \frac{1}{{2\sqrt {hx - {x^2}} }} \cdot {\left( {hx - {x^2}} \right)^\prime } } = {\frac{{h - 2x}}{{\sqrt {hx - {x^2}} }} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {h - 2x = 0}\\ {h - x \ne 0} \end{array}} \right.,}\;\; {\Rightarrow x = \frac{h}{2}.} \] Очевидно, что данная точка является точкой максимума, поскольку при переходе через это значение производная меняет знак с плюса на минус. Таким образом, отверстие для вытекающей жидкости должно располагаться ровно в середине столба жидкости. В этом случае дальность струи будет наибольшей и равной высоте столба жидкости: \[ {{y_{\max }} = 2\sqrt {h \cdot \frac{h}{2} - {{\left( {\frac{h}{2}} \right)}^2}} } = {2\sqrt {\frac{{{h^2}}}{2} - \frac{{{h^2}}}{4}} } = {2\sqrt {\frac{{{h^2}}}{4}} } = {\frac{{\cancel{2}h}}{\cancel{2}} = h.} \] (красивый ответ, не так ли?). |
||||||
|
Пример 9
|
||||||
|
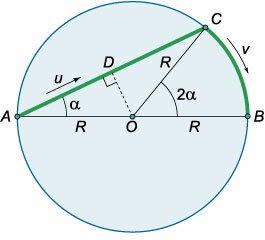
Турист хочет перебраться через озеро круговой формы из точки \(A\) в диаметрально противоположную точку \(B.\) Это можно сделать, плывя на лодке или двигаясь пешком вдоль береговой линии. Определить наиболее быстрый маршрут, если скорость движения лодки \(u,\) а скорость ходьбы \(v.\)
Решение. В случае равенства этих отношений оба маршрута с точки зрения затраченного времени будут равноценны.
|
||||||
|
Пример 10
|
||||||
|
Автомобиль \(A\) движется в северном направлении со скоростью \(u\) (км/час), а автомобиль \(B\) − в западном направлении со скоростью \(v\) (км/час). В начальный момент автомобиль \(B\) находится от автомобиля \(A\) на расстоянии \(b\) (км) строго в восточном направлении. Определить наименьшее расстояние между автомобилями.
Решение. Расстояние между автомобилями вычисляется по теореме Пифагора: \[ {d = \sqrt {{{\left| {OA} \right|}^2} + {{\left| {OB} \right|}^2}} } = {\sqrt {{{\left( {0 - \left( {b - vt} \right)} \right)}^2} + {{\left( {ut - 0} \right)}^2}} } = {\sqrt {{b^2} - 2bvt + {v^2}{t^2} + {u^2}{t^2}}\;\text{(км)}. } \] Исследуем экстремальные значения функции \(d\left( t \right).\) Вычислим производную: \[ {d'\left( t \right) } = {{\left( {\sqrt {{b^2} - 2bvt + {v^2}{t^2} + {u^2}{t^2}} } \right)^\prime } } = {\frac{{ - 2bv + 2\left( {{v^2} + {u^2}} \right)t}}{{2\sqrt {{b^2} - 2bvt + {v^2}{t^2} + {u^2}{t^2}} }} } = {\frac{{\left( {{v^2} + {u^2}} \right)t - bv}}{{\sqrt {{b^2} - 2bvt + {v^2}{t^2} + {u^2}{t^2}} }}.} \] Производная равна нулю в следующий момент времени: \[ {d'\left( t \right) = 0,}\;\; {\Rightarrow \frac{{\left( {{v^2} + {u^2}} \right)t - bv}}{{\sqrt {{b^2} - 2bvt + {v^2}{t^2} + {u^2}{t^2}} }} = 0,}\;\; {\Rightarrow \left( {{v^2} + {u^2}} \right)t - bv = 0,}\;\; {\Rightarrow t = \frac{{bv}}{{{v^2} + {u^2}}}\;\text{(часов)}.} \] Знаменатель производной равен удвоенному расстоянию \(d\left( t \right)\) и всегда положителен. Числитель, а следовательно, и вся производная при переходе через данное значение меняют знак с минуса на плюс. Следовательно, найденное значение \(t\) является точкой минимума. В этот момент расстояние между автомобилями будет наименьшим. Оно определяется следующей формулой: \[ {{d_{\min }} = \sqrt {{b^2} - 2bv\left( {\frac{{bv}}{{{v^2} + {u^2}}}} \right) + \left( {{v^2} + {u^2}} \right){{\left( {\frac{{bv}}{{{v^2} + {u^2}}}} \right)}^2}} } = {\sqrt {{b^2} - \frac{{2{b^2}{v^2}}}{{{v^2} + {u^2}}} + \frac{{{b^2}{v^2}}}{{{v^2} + {u^2}}}} } = {\sqrt {{b^2} - \frac{{{b^2}{v^2}}}{{{v^2} + {u^2}}}} } = {b\sqrt {\frac{{\cancel{v^2} + {u^2} - \cancel{v^2}}}{{{v^2} + {u^2}}}} } = {\frac{{bu}}{{\sqrt {{v^2} + {u^2}} }}\;\text{(км).} } \] |
||||||