|
Устойчивость в первом приближении
|
||||||
|
Рассмотрим автономную систему \(n\) дифференциальных уравнений: \[ {\frac{{d{x_i}}}{{dt}} = {f_i}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),}\;\; {i = 1,2, \ldots ,n.} \] В векторной форме она записывается как \[ {\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right),}\;\; {\text{где}\;\;\mathbf{X} = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right),}\;\; {\mathbf{f} = \left( {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_n}} \end{array}} \right).} \] Будем считать, что данная система имеет положение равновесия \(\mathbf{X} = \mathbf{0},\) которое будем исследовать на устойчивость. Предполагается, что функции \({f_i}\left( \mathbf{X} \right)\) дважды непрерывно дифференцируемы в некоторой окрестности начала координат. Поэтому эти функции можно разложить в ряд Маклорена по переменным \({x_i},\) выделив линейные члены. В результате система уравнений будет иметь следующий вид: \[ {\frac{{d{x_i}}}{{dt}} = \frac{{\partial {f_i}}}{{\partial {x_1}}}\left( 0 \right){x_1} + \frac{{\partial {f_i}}}{{\partial {x_2}}}\left( 0 \right){x_2} + \cdots } + {\frac{{\partial {f_i}}}{{\partial {x_n}}}\left( 0 \right){x_n} } + {{R_i}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right).} \] Здесь слагаемые \({R_i}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)\) описывают члены второго порядка малости относительно переменных \({{x_1},{x_2}, \ldots ,{x_n}}.\)
Полученная система в векторно-матричной записи выглядит так: \[\mathbf{X'} = J\mathbf{X} + \mathbf{R}\left( \mathbf{X} \right),\] где якобиан \(J\) определяется матрицей \[J = \left( {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial {x_1}}}}&{\frac{{\partial {f_1}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_1}}}{{\partial {x_n}}}}\\ {\frac{{\partial {f_2}}}{{\partial {x_1}}}}&{\frac{{\partial {f_2}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_2}}}{{\partial {x_n}}}}\\ \cdots & \cdots & \vdots & \cdots \\ {\frac{{\partial {f_n}}}{{\partial {x_1}}}}&{\frac{{\partial {f_n}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_n}}}{{\partial {x_n}}}} \end{array}} \right).\] Значения частных производных в этой матрице вычисляются в точке разложения в ряд, т.е. в данном случае при \(\mathbf{X} = \mathbf{0}.\) При исследовании на устойчивость вместо исходной нелинейной системы мы можем рассматривать линеаризованную систему \[\mathbf{X'} = J\mathbf{X},\] которая называется системой уравнений первого приближения по отношению к исходной системе. Вопрос о том, в каких случаях исходная нелинейная система и соответствующая система уравнений первого приближения имеют одинаковый характер устойчивости был разрешен А.М.Ляпуновым (\(1857-1918\)). Справедливы следующие теоремы: Теорема Ляпунова об устойчивости по первому приближению. Если все собственные значения \({\lambda _i}\) якобиана \(J\) имеют отрицательные действительные части, то нулевое решение \(\mathbf{X} = \mathbf{0}\) исходной системы и линеаризованной системы является асимптотически устойчивым. Теорема Ляпунова о неустойчивости по первому приближению. Если хотя бы одно собственное значение \({\lambda _i}\) якобиана \(J\) имеет положительную действительную часть, то нулевое решение \(\mathbf{X} = \mathbf{0}\) исходной системы и линеаризованной системы является неустойчивым. В критических случаях, когда действительные части всех собственных значений \({\lambda _i}\) якобиана \(J\) неположительны, причем существует хотя бы одно собственное значение с нулевой действительной частью, нулевое решение может быть устойчивым или неустойчивым. В этом случае выяснить характер устойчивости в рамках первого приближения невозможно и необходимо использовать другие методы исследования устойчивости. Итак, приведенные теоремы Ляпунова позволяют исследовать устойчивость нулевого решения нелинейных систем в тех случаях, когда положение равновесия характеризуется собственными значениями с ненулевой действительной частью. Такие точки равновесия называются грубыми. Более точное определение формулируется так: Положение равновесия \(\mathbf{X} = \mathbf{0}\) автономной системы \(n\)-го порядка \[\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right)\] называется грубым, если соответствующий якобиан \(J\) имеет ровно \(n\) попарно различных собственных значений с ненулевой действительной частью. Заметим, что в случае системы \(2\)-го порядка только следующие \(3\) типа точек равновесия являются грубыми: 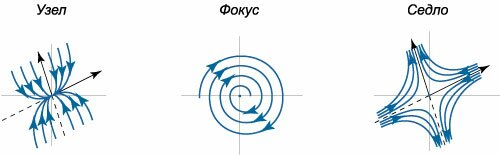 Таким образом, область применения метода исследования устойчивости по первому приближению ограничена грубыми (или структурно устойчивыми) системами. |
||||||
|
Пример 1
|
||||||
|
Исследовать на устойчивость по первому приближению нулевое положение равновесия системы \[\frac{{dx}}{{dt}} = y + 3{x^2} + 2{y^2},\;\;\frac{{dy}}{{dt}} = - 2x - y + xy.\]
Решение.
В данном случае функции \({f_1},{f_2}\) имеют вид: \[ {{f_1}\left( {x,y} \right) = y + 3{x^2} + 2{y^2},}\;\; {{f_2}\left( {x,y} \right) = - 2x - y + xy.} \] Очевидно, они непрерывны и бесконечно дифференцируемы в окрестности начала координат и равны нулю при \(\mathbf{X} = \mathbf{0}.\) Кроме того, порядок нелинейных членов в обеих функциях равен или больше \(2.\) Тем самым, выполнены все требования теоремы об устойчивости по первому приближению. Вычислим элементы якобиана \(J\) в точке равновесия \(\mathbf{X} = \mathbf{0}:\) \[ {\frac{{\partial {f_1}}}{{\partial x}} = 6x,}\;\; {\frac{{\partial {f_1}}}{{\partial y}} = 1 + 6y,}\;\; {\frac{{\partial {f_2}}}{{\partial x}} = - 2 + y,}\;\; {\frac{{\partial {f_2}}}{{\partial y}} = - 1 + x,} \] \[\require{AMSmath.js} {\Rightarrow {\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\substack{ x = 0\\ y = 0}}} = 0,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial y}}} \right|_{\substack{ x = 0\\ y = 0}}} = 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial x}}} \right|_{\substack{ x = 0\\ y = 0}}} = - 2,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial y}}} \right|_{\substack{ x = 0\\ y = 0}}} = - 1,}\;\; {\Rightarrow J = \left( {\begin{array}{*{20}{r}} 0&1\\ { - 2}&{ - 1} \end{array}} \right).} \] Найдем собственные значения: \[ {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {0 - \lambda }&1\\ { - 2}&{ - 1 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \lambda \left( {\lambda + 1} \right) + 2 = 0,}\;\; {\Rightarrow {\lambda ^2} + \lambda + 2 = 0,}\;\; {\Rightarrow D = - 7,}\;\; {\Rightarrow {\lambda _{1,2}} = \frac{{ - 1 \pm \sqrt { - 7} }}{2} } = { - \frac{1}{2} \pm \frac{{i\sqrt 7 }}{2}.} \] Характеристическое уравнение имеет пару комплексно сопряженных корней, у которых действительная часть отрицательна: \[\text{Re}\left[ {{\lambda _1}} \right] < 0,\;\;\text{Re}\left[ {{\lambda _2}} \right] < 0.\] Следовательно, нулевое решение данной системы устойчиво по теореме об устойчивости по первому приближению. Данная точка равновесия является фокусом. |
||||||
|
Пример 2
|
||||||
|
Найти положение равновесия системы и исследовать его устойчивость по первому приближению. \[\frac{{dx}}{{dt}} = {x^2} - y,\;\;\frac{{dy}}{{dt}} = x - 1.\]
Решение.
Определим положение равновесия из системы алгебраических уравнений: \[ {\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = 0\\ \frac{{dy}}{{dt}} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{x^2} - y = 0}\\ {x - 1 = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 1}\\ {y = 1} \end{array}} \right..} \] Поскольку точка равновесия \(\left( {1,1} \right)\) не является нулевым решением, выполним преобразование координат. Введем новые переменные \(u, v:\) \[u = x - 1,\;\;v = y - 1.\] После подстановки в исходную систему получаем \[\require{cancel} {\left\{ \begin{array}{l} \frac{{d\left( {u + 1} \right)}}{{dt}} = {\left( {u + 1} \right)^2} - \left( {v + 1} \right)\\ \frac{{d\left( {v + 1} \right)}}{{dt}} = u + \cancel{1} - \cancel{1} \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\frac{{du}}{{dt}} = {u^2} + 2u + \cancel{1} - v - \cancel{1}}\\ {\frac{{dv}}{{dt}} = u} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\frac{{du}}{{dt}} = {u^2} + 2u - v}\\ {\frac{{dv}}{{dt}} = u} \end{array}} \right..} \] Чтобы определить характер устойчивости нулевого решения, вычислим якобиан \(J.\) Правые части имеют вид: \[{f_1}\left( {u,v} \right) = {u^2} + 2u - v,\;\;{f_2}\left( {u,v} \right) = u.\] Тогда \[ {\frac{{\partial {f_1}}}{{\partial u}} = 2u + 2,}\;\; {\frac{{\partial {f_1}}}{{\partial v}} = - 1,}\;\; {\frac{{\partial {f_2}}}{{\partial u}} = 1,}\;\; {\frac{{\partial {f_2}}}{{\partial v}} = 0.} \] Соответственно, в точке \(\left( {u = 0,v = 0} \right)\) частные производные имеют следующие значения: \[ {{\left. {\frac{{\partial {f_1}}}{{\partial u}}} \right|_{\substack{ u = 0\\ v = 0}}} = 2,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial v}}} \right|_{\substack{ u = 0\\ v = 0}}} = - 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial u}}} \right|_{\substack{ u = 0\\ v = 0}}} = 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial v}}} \right|_{\substack{ u = 0\\ v = 0}}} = 0.} \] Найдем собственные значения якобиана \(J:\) \[ {J = \left( {\begin{array}{*{20}{r}} 2&{ - 1}\\ 1&0 \end{array}} \right),}\;\; {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {2 - \lambda }&{ - 1}\\ 1&{0 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \lambda \left( {\lambda - 2} \right) + 1 = 0,}\;\; {\Rightarrow {\lambda ^2} - 2\lambda + 1 = 0,}\;\; {\Rightarrow {\left( {\lambda - 1} \right)^2} = 0,}\;\; {\Rightarrow {\lambda _{1,2}} = 1.} \] Таким образом, матрица \(J\) имеет одно собственное значение \(\lambda = 1\) с алгебраической кратностью \(2.\)Согласно определению, грубая точка равновесия должна описываться различными собственными значениями. Поскольку в данном случае это условие нарушено, мы не можем судить о характере устойчивости системы по первому приближению. Для корректного анализа устойчивости здесь требуются другие подходы, например, метод функций Ляпунова. |
||||||
|
Пример 3
|
||||||
|
Определить положения равновесия системы и исследовать их на устойчивость. Построить схематический фазовый портрет соответствующей линеаризованной системы. \[\frac{{dx}}{{dt}} = {e^{x + y}} - 1,\;\;\frac{{dy}}{{dt}} = \ln \left( {1 + x} \right).\]
Решение.
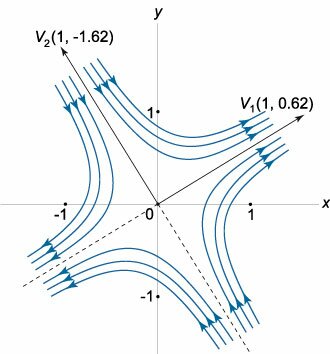
Найдем точки равновесия, решив алгебраическую систему уравнений: \[ {\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = 0\\ \frac{{dy}}{{dt}} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {e^{x + y}} - 1 = 0\\ \ln \left( {1 + x} \right) = 0 \end{array} \right..} \] Из второго уравнения следует, что \(x = 0.\) Подставляя это в первое уравнение, получаем: \[{e^y} - 1 = 0,\;\; \Rightarrow {e^y} = 1,\;\; \Rightarrow y = 0.\] Таким образом, система имеет единственное положение равновесия \(\left( {x = 0,y = 0} \right).\) Для исследования устойчивости нулевого решения разложим правые части уравнений в ряд Маклорена: \[ {{f_1}\left( {x,y} \right) = {e^{x + y}} - 1,}\;\; {{f_2}\left( {x,y} \right) = \ln \left( {1 + x} \right),} \] \[ {\frac{{\partial {f_1}}}{{\partial x}} = {e^{x + y}},}\;\; {\frac{{\partial {f_1}}}{{\partial y}} = {e^{x + y}},}\;\; {\frac{{\partial {f_2}}}{{\partial x}} = \frac{1}{{1 + x}},}\;\; {\frac{{\partial {f_2}}}{{\partial y}} = 0.} \] Частные производные в точке \(\left( {x = 0,y = 0} \right)\) равны: \[ {{\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\substack{ x = 0\\ y = 0}}} = 1,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial y}}} \right|_{\substack{ x = 0\\ y = 0}}} = 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial x}}} \right|_{\substack{ x = 0\\ y = 0}}} = 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial y}}} \right|_{\substack{ x = 0\\ y = 0}}} = 0.} \] Найдем собственные значения матрицы-якобиана \(J:\) \[ {J = \left( {\begin{array}{*{20}{c}} 1&1\\ 1&0 \end{array}} \right),}\;\; {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&1\\ 1&{0 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \lambda \left( {\lambda - 1} \right) - 1 = 0,}\;\; {\Rightarrow {\lambda ^2} - \lambda - 1 = 0,}\;\; {\Rightarrow D = 5,}\;\; {{\lambda _{1,2}} = \frac{{1 \pm \sqrt 5 }}{2} = \frac{1}{2} \pm \frac{{\sqrt 5 }}{2}.} \] Видно, что собственные значения являются действительными числами с разными знаками и приближенно равны \[ {{\lambda _1} = \frac{1}{2} + \frac{{\sqrt 5 }}{2} \approx 0.5 + 1.12 = 1.62,}\;\;\; {{\lambda _2} = \frac{1}{2} - \frac{{\sqrt 5 }}{2} \approx 0.5 - 1.12 = - 0.62} \] Следовательно, линеаризованная система имеет нулевое положение равновесия типа седло. Аналогичный вывод справедлив и в отношении исходной нелинейной системы.Построим схематический фазовый портрет линеаризованной системы. Вычислим собственные векторы \({\mathbf{V}_1},\) \({\mathbf{V}_2},\) ассоциированные с собственными значениями \({\lambda _1}\) и \({\lambda _2}.\) Для первого собственного значения \({\lambda _1}\) получаем: \[ {\left( {J - {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {1 - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right)}&1\\ 1&{ - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {\frac{1}{2} - \frac{{\sqrt 5 }}{2}}&1\\ 1&{ - \frac{1}{2} - \frac{{\sqrt 5 }}{2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0}\\ {{V_{11}} - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{21}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0}\\ {\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right)\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{21}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0}\\ {\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} + {V_{21}} = 0.} \] Пусть \({V_{11}} = t.\) Тогда \[ {{V_{21}} = - \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{11}} } = {- \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right)t \approx 0.62t,}\;\; {\Rightarrow {\mathbf{V}_1} = \left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} t\\ {0.62t} \end{array}} \right) } = {t\left( {\begin{array}{*{20}{c}} 1\\ {0.62} \end{array}} \right) \sim \left( {\begin{array}{*{20}{c}} 1\\ {0.62} \end{array}} \right).} \] Аналогично находим собственный вектор \({\mathbf{V}_2},\) соответствующий числу \({\lambda _2}:\) \[ {\left( {J - {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {1 - \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right)}&1\\ 1&{ - \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{{\sqrt 5 }}{2}}&1\\ 1&{ - \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0}\\ {{V_{12}} - \left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{22}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0}\\ {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right)\left( {\frac{1}{2} - \frac{{\sqrt 5 }}{2}} \right){V_{22}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0}\\ {\left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0} \end{array}} \right.,}\;\; {\Rightarrow \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} + {V_{22}} = 0.} \] Пусть \({V_{12}} = t.\) Следовательно, \[ {{V_{22}} = - \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right){V_{12}} } = {- \left( {\frac{1}{2} + \frac{{\sqrt 5 }}{2}} \right)t \approx -1.62t,}\;\; {\Rightarrow {\mathbf{V}_2} = \left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} t\\ {-1.62t} \end{array}} \right) } = {t\left( {\begin{array}{*{20}{c}} 1\\ {-1.62} \end{array}} \right) \sim \left( {\begin{array}{*{20}{c}} 1\\ {-1.62} \end{array}} \right).} \] Построим на фазовой плоскости прямые, проходящие через начало координат и направленные вдоль векторов \({\mathbf{V}_1}\) и \({\mathbf{V}_2}\) (рисунок \(1\)). Эти прямые являются сепаратрисами седла. Схематически изобразим фазовые траектории.
Данная точка равновесия является грубой. Поэтому фазовый портрет исходной нелинейной системы имеет такой же вид в окрестности нуля, как и портрет линеаризованной системы, показанной на рис.\(1.\) |
||||||
|
Пример 4
|
||||||
|
Исследовать нулевое решение системы на устойчивость по первому приближению. \[ {\frac{{dx}}{{dt}} = \tan \left( {x + y} \right) - y,}\;\; {\frac{{dy}}{{dt}} = 3\sin x + 2{e^y} - 2.} \]
Решение.
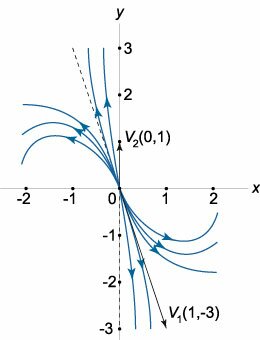
Убедимся, что точка \(\left( {x = 0,y = 0} \right)\) является положением равновесия для заданной системы: \[ {{f_1}\left( {0,0} \right) = \tan 0 - 0 = 0,}\;\; {{f_2}\left( {0,0} \right) = 3\sin 0 + 2{e^0} - 2 } = {0 + 2 \cdot 1 - 2 = 0.} \] Разложим функции \({f_1},{f_2}\) (которые являются непрерывно дифференцируемыми в окрестности нуля) в ряд Маклорена. Частные производные первого порядка имеют вид: \[ {\frac{{\partial {f_1}}}{{\partial x}} = \frac{1}{{{{\cos }^2}\left( {x + y} \right)}},}\;\; {\frac{{\partial {f_1}}}{{\partial y}} = \frac{1}{{{{\cos }^2}\left( {x + y} \right)}} - 1,}\;\; {\frac{{\partial {f_2}}}{{\partial x}} = 3\cos x,}\;\; {\frac{{\partial {f_2}}}{{\partial y}} = 2{e^y}.} \] Значения производных в точке \(\left( {x = 0,y = 0} \right)\) равны \[ {{\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\left( {0,0} \right)}} = 1,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial y}}} \right|_{\left( {0,0} \right)}} = 0,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial x}}} \right|_{\left( {0,0} \right)}} = 3,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial y}}} \right|_{\left( {0,0} \right)}} = 2.} \] Следовательно, для линеаризованной системы мы получили матрицу Якоби следующего вида: \[J = \left( {\begin{array}{*{20}{c}} 1&0\\ 3&2 \end{array}} \right).\] Вычислим ее собственные значения: \[ {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&0\\ 3&{2 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( {\lambda - 1} \right)\left( {\lambda - 2} \right) = 0,}\;\; {\Rightarrow {\lambda _1} = 1,\;{\lambda _2} = 2.} \] Таким образом, согласно теореме Ляпунова об устойчивости по первому приближению нулевое решение данной системы неустойчиво и представляет собой неустойчивый узел.Найдем соответствующие собственные векторы и начертим схематический фазовый портрет линеаризованной системы вблизи нуля. Для собственного значения \({\lambda _1} = 1\) вектор \({\mathbf{V}_1}\) имеет следующие координаты: \[ {\left( {J - {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {1 - 1}&0\\ 3&{2 - 1} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} 0&0\\ 3&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow 3{V_{11}} + {V_{21}} = 0.} \] Пусть \({V_{11}} = t.\) Тогда \[ {{V_{21}} = - 3{V_{11}} = - 3t,}\;\; {\Rightarrow {\mathbf{V}_1} = \left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} t\\ { - 3t} \end{array}} \right) } = {t\left( {\begin{array}{*{20}{c}} 1\\ { - 3} \end{array}} \right) } \sim {\left( {\begin{array}{*{20}{c}} 1\\ { - 3} \end{array}} \right).} \] Определим собственный вектор \({\mathbf{V}_2}\) для собственного значения \({\lambda _2} = 2:\) \[ {\left( {J - {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {1 - 2}&0\\ 3&{2 - 2} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{r}} { - 1}&0\\ 3&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} { - {V_{12}} + 0 \cdot {V_{22}} = 0}\\ {3{V_{12}} + 0 \cdot {V_{22}} = 0} \end{array}} \right..} \] Полагаем \({V_{12}} = 0,\) \({V_{22}} = 1,\) т.е. \[{\mathbf{V}_2} = \left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} \right).\] Изобразим на фазовой плоскости асимптотические прямые, проходящие через начало координат и параллельные найденным векторам \({\mathbf{V}_1}\) и \({\mathbf{V}_2}\) (рис.\(2\) выше). Учтем, что фазовые траектории асимптотически приближаются к прямой, направленной вдоль вектора \({\mathbf{V}_1},\) которому соответствует наименьшее по модулю собственное значение \({\lambda _1} = 1.\) При удалении от начала координат фазовые траектории становятся параллельными оси \(Oy,\) вдоль которой направлен собственный вектор \({\mathbf{V}_2}.\) Такой же фазовый портрет в окрестности начала координат имеет и исходная нелинейная система. Это следует из свойства грубости (структурной устойчивости) нулевого положения равновесия. |
||||||
|
Пример 5
|
||||||
|
Используя метод первого приближения, исследовать на устойчивость положение равновесия системы \[\frac{{dx}}{{dt}} = \ln \left( {x + y} \right),\;\;\frac{{dy}}{{dt}} = \arctan \frac{{2x}}{y}.\]
Решение.
Определим сначала точку равновесия: \[ {\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = 0\\ \frac{{dy}}{{dt}} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} \ln \left( {x + y} \right) = 0\\ \arctan \frac{{2x}}{y} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {x + y = 1}\\ {x + y > 0}\\ {\frac{{2x}}{y} = 0}\\ {y \ne 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {x + y = 1}\\ {x = 0}\\ {x + y > 0}\\ {y \ne 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 0}\\ {y = 1} \end{array}} \right..} \] Таким образом, система имеет одно положение равновесия в точке \(\left( {x = 0,y = 1} \right).\) Исследуем его на устойчивость с помощью системы первого приближения. Вычислим частные производные правых частей \({f_1}\left( {x,y} \right)\) и \({f_2}\left( {x,y} \right).\) \[\frac{{\partial {f_1}}}{{\partial x}} = \frac{\partial }{{\partial x}}\left[ {\ln \left( {x + y} \right)} \right] = \frac{1}{{x + y}},\] \[\frac{{\partial {f_1}}}{{\partial y}} = \frac{\partial }{{\partial y}}\left[ {\ln \left( {x + y} \right)} \right] = \frac{1}{{x + y}},\] \[ {\frac{{\partial {f_2}}}{{\partial x}} = \frac{\partial }{{\partial x}}\left[ {\arctan\frac{{2x}}{y}} \right] } = {\frac{1}{{1 + {{\left( {\frac{{2x}}{y}} \right)}^2}}} \cdot \frac{2}{y} } = {\frac{{{y^2}}}{{{y^2} + 4{x^2}}} \cdot \frac{2}{y} } = {\frac{{2y}}{{4{x^2} + {y^2}}},} \] \[ {\frac{{\partial {f_2}}}{{\partial y}} = \frac{\partial }{{\partial y}}\left[ {\arctan\frac{{2x}}{y}} \right] } = {\frac{1}{{1 + {{\left( {\frac{{2x}}{y}} \right)}^2}}} \cdot \left( { - \frac{{2x}}{{{y^2}}}} \right) } = {\frac{{{y^2}}}{{{y^2} + 4{x^2}}} \cdot \left( { - \frac{{2x}}{{{y^2}}}} \right) } = { - \frac{{2x}}{{4{x^2} + {y^2}}}.} \] В точке \(\left( {x = 0,y = 1} \right)\) производные имеют следующие значения: \[ {{\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\left( {0,1} \right)}} = 1,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial y}}} \right|_{\left( {0,1} \right)}} = 1,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial x}}} \right|_{\left( {0,1} \right)}} = 2,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial y}}} \right|_{\left( {0,1} \right)}} = 0.} \] Следовательно, линеаризованная матрица (якобиан) в точке равновесия выглядит так: \[J = \left( {\begin{array}{*{20}{c}} 1&1\\ 2&0 \end{array}} \right).\] Найдем ее собственные значения \(\lambda:\) \[ {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&1\\ 2&{0 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \lambda \left( {\lambda - 1} \right) - 2 = 0,}\;\; {\Rightarrow {\lambda ^2} - \lambda - 2 = 0,}\;\; {\Rightarrow D = 9,}\;\; {{\lambda _{1,2}} = \frac{{1 \pm 3}}{2} = - 1,2.} \] Итак, положение равновесия \(\left( {0,1} \right)\) линеаризованной системы характеризуется двумя действительными собственными значениями разного знака. Это значит, в соответствии с теоремой о неустойчивости по первому приближению, что точка \(\left( {0,1} \right)\) неустойчива. Данная точка равновесия является седлом. |
||||||
|
Пример 6
|
||||||
|
Используя систему уравнений первого приближения, исследовать на устойчивость нулевое решение системы \[\frac{{dx}}{{dt}} = \sin \left( {x + y} \right) - y,\;\;\frac{{dy}}{{dt}} = {y^2} + 2x.\]
Решение.
Очевидно, что правые части дифференциальных уравнений непрерывны и дифференцируемы бесконечное число раз. Следовательно, можно выполнить разложение в ряд Маклорена: \[ {{f_1}\left( {x,y} \right) = \sin \left( {x + y} \right) - y,}\;\;\; {{f_2}\left( {x,y} \right) = {y^2} + 2x,} \] \[ {\frac{{\partial {f_1}}}{{\partial x}} = \cos \left( {x + y} \right),}\;\; {\frac{{\partial {f_1}}}{{\partial y}} = \cos \left( {x + y} \right) - 1,}\;\; {\frac{{\partial {f_2}}}{{\partial x}} = 2,}\;\; {\frac{{\partial {f_2}}}{{\partial y}} = 2y.} \] Подставляя \(x = 0, y = 0,\) получаем следующие значения производных: \[ {{\left. {\frac{{\partial {f_1}}}{{\partial x}}} \right|_{\left( {0,0} \right)}} = 1,}\;\; {{\left. {\frac{{\partial {f_1}}}{{\partial y}}} \right|_{\left( {0,0} \right)}} = 0,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial x}}} \right|_{\left( {0,0} \right)}} = 2,}\;\; {{\left. {\frac{{\partial {f_2}}}{{\partial y}}} \right|_{\left( {0,0} \right)}} = 0.} \] Составим матрицу-якобиан \(J\) и вычислим ее собственные значения: \[ {J = \left( {\begin{array}{*{20}{c}} 1&0\\ 2&0 \end{array}} \right),}\;\; {\det \left( {J - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&0\\ 2&{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \lambda \left( {\lambda - 1} \right) = 0,}\;\; {\Rightarrow {\lambda _1} = 0,\;{\lambda _2} = 1.} \] Мы получили два собственных значения, одно из которых равно нулю. Это означает, что мы имеем критический случай, для которого невозможно определить характер устойчивости точки равновесия в рамках первого приближения. |
||||||