Уравнения, решаемые в квадратурах

Говорят, что дифференциальное уравнение решается в квадратурах, если его общее решение выражается через один или несколько интегралов.

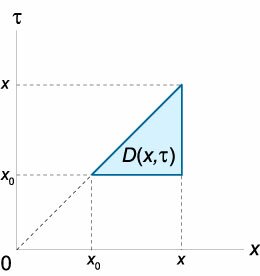
Далее мы рассмотрим три типа уравнений высшего порядка, которые интегрируются в квадратурах. Предположим сначала, что данное уравнение можно преобразовать в явную форму относительно производной \({{y^{\left( n \right)}}},\) т.е. выразить в виде \[{y^{\left( n \right)}} = f\left( x \right).\] Проинтегрируем это уравнение последовательно \(n\) раз в пределах от \({x_0}\) до \(x.\) Получаем следующие выражения для производных и для самой функции \(y\left( x \right):\) \[{y^{\left( {n - 1} \right)}}\left( x \right) = \int\limits_{{x_0}}^x {f\left( x \right)dx} + {C_1},\] \[{y^{\left( {n - 2} \right)}}\left( x \right) = \int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {f\left( x \right)dx} + {C_1}\left( {x - {x_0}} \right) + {C_2},\] \[\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\] \[ {y\left( x \right) = \underbrace {\int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {dx} \cdots \int\limits_{{x_0}}^x {f\left( x \right)dx} }_{n\;\text{раз}} } + {{C_1}\frac{{{{\left( {x - {x_0}} \right)}^{n - 1}}}}{{\left( {n - 1} \right)!}} + \cdots } + {{C_{n - 1}}\left( {x - {x_0}} \right) + {C_n}.} \] Последняя формула представляет собой общее решение дифференциального уравнения в квадратурах. При \(x = {x_0}\) мы получим частное решение, удовлетворяющее начальным условиям \[ {y\left( {x = {x_0}} \right) = {C_n},}\;\; {y'\left( {x = {x_0}} \right) = {C_{n - 1}},\;\; \ldots,}\;\; {{y^{\left( {n - 2} \right)}}\left( {x = {x_0}} \right) = {C_2},}\;\; {{y^{\left( {n - 1} \right)}}\left( {x = {x_0}} \right) = {C_1},} \] где \({C_1},{C_2}, \ldots ,{C_n}\) − некоторый заданный набор чисел.

Повторный интеграл в выражении для \(y\left( x \right)\) можно преобразовать к однократному интегралу. Действительно, в случае \(n = 2\) рассмотрим интеграл \[y\left( x \right) = \int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {f\left( \tau \right)d\tau } ,\] в котором через \(\tau\) обозначена переменная интегрирования во внутреннем интеграле.

Данный повторный интеграл задан в треугольной области \(D\left( {x,\tau } \right),\) изображенной на рисунке \(1.\) В этом интеграле можно поменять порядок интегрирования, используя формулу Дирихле: \[ {y\left( x \right) = \int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {f\left( \tau \right)d\tau } } = {\int\limits_{{x_0}}^x {f\left( \tau \right)d\tau } \int\limits_\tau ^x {dx} .} \] В результате двукратный интеграл сводится к однократному: \[ {y\left( x \right) = \int\limits_{{x_0}}^x {f\left( \tau \right)\left( {x - \tau } \right)d\tau } } = {\int\limits_{{x_0}}^x {\frac{{\left( {x - \tau } \right)}}{{1!}}f\left( \tau \right)d\tau } .} \] Аналогичным образом можно упростить трехкратный повторный интеграл в случае \(n = 3:\) \[ {y\left( x \right) = \int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {f\left( x \right)dx} } = {\int\limits_{{x_0}}^x {dx} \int\limits_{{x_0}}^x {\frac{{\left( {x - \tau } \right)}}{{1!}}f\left( \tau \right)d\tau } } = {\int\limits_{{x_0}}^x {f\left( \tau \right)d\tau } \int\limits_\tau ^x {\frac{{\left( {x - \tau } \right)}}{{1!}}d\tau } } = {\int\limits_{{x_0}}^x {\left[ {\left. {\left( {\frac{{{{\left( {x - \tau } \right)}^2}}}{{2!}}} \right)} \right|_{x = \tau }^{x = x}} \right]f\left( \tau \right)d\tau } } = {\int\limits_{{x_0}}^x {\frac{{{{\left( {x - \tau } \right)}^2}}}{{2!}}f\left( \tau \right)d\tau } .} \] Для повторного интеграла произвольной кратности \(n\) будет справедливо выражение \[y\left( x \right) = \int\limits_{{x_0}}^x {\frac{{{{\left( {x - \tau } \right)}^{n - 1}}}}{{\left( {n - 1} \right)!}}f\left( \tau \right)d\tau } ,\] которое называется формулой Коши для повторных интегралов.

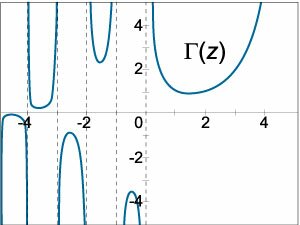
Полученное выражение представляет собой частное решение дифференциального уравнения \({y^{\left( n \right)}} = f\left( x \right)\) при нулевых начальных условиях \[ {y\left( {x = {x_0}} \right) = 0,}\;\; {y'\left( {x = {x_0}} \right) = 0,\;\; \ldots ,}\;\; {{y^{\left( {n - 1} \right)}}\left( {x = {x_0}} \right) = 0.} \] Соответственно, общее решение исходного уравнения описывается формулой \[ {y\left( x \right) = \int\limits_{{x_0}}^x {\frac{{{{\left( {x - \tau } \right)}^{n - 1}}}}{{\left( {n - 1} \right)!}}f\left( \tau \right)d\tau } } + {{C_1}\frac{{{{\left( {x - {x_0}} \right)}^{n - 1}}}}{{\left( {n - 1} \right)!}} + \cdots } + {{C_{n - 1}}\left( {x - {x_0}} \right) + {C_n}.} \] Заметим, что формула Коши связывает между собой функцию \(y\left( x \right)\) и ее производную \(n\)-го порядка \({y^{\left( n \right)}} = f\left( x \right).\) Если допустить, что число \(n\) может быть действительным, то мы приходим к понятию производной дробного порядка.

Вместо факториала \(\left( {n - 1} \right)!\) в формуле Коши запишем так называемую гамма-функцию \(\Gamma \left( z \right),\) которая является непрерывной и выражается через несобственный интеграл в виде \[\Gamma \left( z \right) = \int\limits_0^\infty {{e^{ - t}}{t^{z - 1}}dt} .\] Вид гамма-функции \(\Gamma \left( z \right)\) для действительных значений \(z\) показан выше на рисунке \(2.\) При натуральных значениях \(n\) справедливо равенство \[\Gamma \left( n \right) = \left( {n - 1} \right)!\] Тогда формула Коши представляется в следующем виде: \[y\left( {x,z} \right) = \int\limits_{{x_0}}^x {\frac{{{{\left( {x - \tau } \right)}^{z - 1}}}}{{\Gamma \left( z \right)}}f\left( \tau \right)d\tau } .\] где \(z\) − действительное число.

Данную формулу можно рассматривать как определение дробной производной порядка \(z,\) если исходная функция \(y\left( x \right)\) известна или как определение интеграла дробного порядка \(z,\) если задана соответствующая производная.

Мы рассмотрели решение явного дифференциального уравнения \({y^{\left( n \right)}} = f\left( x \right)\) в квадратурах. Неявное уравнение \(F\left( {x,{y^{\left( n \right)}}} \right) = 0\) также можно проинтегрировать, если его удается разрешить относительно переменной \(x\) или, в более общем случае, представить в параметрической форме: \[x = \varphi \left( t \right),\;\;{y^{\left( n \right)}} = \psi \left( t \right).\] Тогда, учитывая, что \[d{y^{\left( {n - 1} \right)}} = {y^{\left( n \right)}}dx = \psi \left( t \right)\varphi '\left( t \right)dt,\] получаем \[{y^{\left( {n - 1} \right)}}\left( x \right) = \int {\psi \left( t \right)\varphi '\left( t \right)dt} + {C_1}.\] Далее аналогичным образом находим остальные производные и саму функцию \(y\left( x \right).\) В результате получаем общее решение уравнения в параметрическом виде: \[x = \varphi \left( t \right),\;\;y = \Phi \left( {t,{C_1},{C_2}, \ldots ,{C_n}} \right).\] Рассмотрим сначала случай, когда такое уравнение можно разрешить относительно \({{y^{\left( n \right)}}}:\) \[{y^{\left( n \right)}} = f\left( {{y^{\left( {n - 1} \right)}}} \right).\] Решаем его следующим образом. Вводим новую переменную \(z = {{y^{\left( {n - 1} \right)}}}.\) Тогда уравнение записывается как \[z' = f\left( z \right).\] Разделяя переменные, находим его общее решение: \[\int {\frac{{dz}}{{f\left( z \right)}}} = x + {C_1},\;\; \Rightarrow z = \varphi \left( {x,{C_1}} \right).\] Возвращаясь к переменной \(y,\) получаем дифференциальное уравнение \(\left( {n - 1} \right)\)-го порядка: \[{y^{\left( {n - 1} \right)}} = \varphi \left( {x,{C_1}} \right).\] которое решается методом, изложенном выше в пункте \(1.\)

Общее неявное уравнение \(F\left( {{y^{\left( {n - 1} \right)}},{y^{\left( n \right)}}} \right) = 0\) можно проинтегрировать, если оно представляется в параметрической форме \[{y^{\left( n \right)}} = \varphi \left( t \right),\;\;{y^{\left( {n - 1} \right)}} = \psi \left( t \right).\] Поскольку \(d{y^{\left( {n - 1} \right)}} = {y^{\left( n \right)}}dx,\) получаем следующее выражение для \(x\left( t \right):\) \[ {dx = \frac{{d{y^{\left( {n - 1} \right)}}}}{{{y^{\left( n \right)}}}} = \frac{{\psi '\left( t \right)dt}}{{\varphi \left( t \right)}},}\;\; {\Rightarrow x = \int {\frac{{\psi '\left( t \right)dt}}{{\varphi \left( t \right)}}} + {C_1}.} \] Выражение для \(y\left( t \right)\) находится последовательным интегрированием: \[ {d{y^{\left( {n - 2} \right)}} = {y^{\left( {n - 1} \right)}}dx = \frac{{\psi \left( t \right)\psi '\left( t \right)dt}}{{\varphi \left( t \right)}},}\;\; {\Rightarrow {y^{\left( {n - 2} \right)}} = \int {\frac{{\psi \left( t \right)\psi '\left( t \right)dt}}{{\varphi \left( t \right)}}} + {C_2},} \] \[\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\] \[dy = y'dx,\;\; \Rightarrow y = \int {y'dx} + {C_n}.\] В результате мы получаем общее решение уравнения в параметрическом виде. Предположим, что данное уравнение разрешено относительно \({{y^{\left( n \right)}}}:\) \[{y^{\left( n \right)}} = f\left( {{y^{\left( {n - 2} \right)}}} \right).\] Вводя новую переменную \({{y^{\left( {n - 2} \right)}}} = z,\) запишем его как \[z'' = f\left( z \right).\] Умножая обе части на \(z'\) (в предположении, что уравнение не имеет решения \(z' = 0\)), получаем: \[ {z'z'' = f\left( z \right)z',}\;\; {\Rightarrow d\left[ {{{\left( {z'} \right)}^2}} \right] = 2f\left( z \right)dz,}\;\; {\Rightarrow {\left( {z'} \right)^2} = 2\int {f\left( z \right)dz} + {C_1},}\;\; {\Rightarrow z' = \sqrt {2\int {f\left( z \right)dz} + {C_1}} ,}\;\; {\Rightarrow {y^{\left( {n - 1} \right)}} = \sqrt {2\int {f\left( {{y^{\left( {n - 2} \right)}}} \right)d{y^{\left( {n - 2} \right)}}} + {C_1}} .} \] Видно, что мы получили уравнение вида \({y^{\left( {n - 1} \right)}} = f\left( {{y^{\left( {n - 2} \right)}}} \right),\) которое было рассмотрено в пункте \(2\) и которое решается в квадратурах.

Если уравнение \(z'' = f\left( z \right)\) имеет решение \(z' = 0,\) то общее решение выражается формулой: \[ {{y^{\left( {n - 1} \right)}} = 0,}\;\; {\Rightarrow y = {C_1}{x^{n - 2}} + {C_2}{x^{n - 3}} + \cdots + {C_{n - 1}}.} \] В случае, когда дифференциальное уравнение \(F\left( {{y^{\left( {n - 2} \right)}},{y^{\left( n \right)}}} \right) = 0\) допускает параметрическое представление \[{y^{\left( n \right)}} = \varphi \left( t \right),\;\;{y^{\left( {n - 2} \right)}} = \psi \left( t \right),\] его решение строится следующим образом. Из соотношений \[d{y^{\left( {n - 1} \right)}} = {y^{\left( n \right)}}dx,\;\;d{y^{\left( {n - 2} \right)}} = {y^{\left( {n - 1} \right)}}dx\] следует, что \[{y^{\left( {n - 1} \right)}}d{y^{\left( {n - 1} \right)}} = {y^{\left( n \right)}}d{y^{\left( {n - 2} \right)}},\] или в параметрической форме: \[{y^{\left( {n - 1} \right)}}d{y^{\left( {n - 1} \right)}} = \varphi \left( t \right)\psi '\left( t \right)dt.\] Интегрируя, находим: \[{y^{\left( {n - 1} \right)}} = \sqrt {2\int {\varphi \left( t \right)\psi '\left( t \right)dt} + {C_1}} .\] Теперь мы знаем параметрическое выражение для производных \({y^{\left( {n - 2} \right)}}\) и \({y^{\left( {n - 1} \right)}},\) т.е. задача сводится к типу \(2.\)

   Пример 1

Найти общее решение дифференциального уравнения \(y''' = {x^2} - 1.\)
Данное уравнение относится к типу \({y^{\left( n \right)}} = f\left( x \right)\) при \(n = 3.\) Его общее решение записывается в виде \[ {y\left( x \right) = \int\limits_{{x_0}}^x {\frac{{{{\left( {x - \tau } \right)}^2}}}{{2!}}\left( {{\tau ^2} - 1} \right)d\tau } } + {{C_1}\frac{{{{\left( {x - {x_0}} \right)}^2}}}{{2!}} } + {{C_2}\left( {x - {x_0}} \right) + {C_3}.} \] Вычислим входящий в эту формулу интеграл: \[\require{cancel} {I = \frac{1}{2}\int\limits_{{x_0}}^x {{{\left( {x - \tau } \right)}^2}\left( {{\tau ^2} - 1} \right)d\tau } } = {\frac{1}{2}\int\limits_{{x_0}}^x {\left( {{x^2} - 2x\tau + {\tau ^2}} \right)\left( {{\tau ^2} - 1} \right)d\tau } } = {\frac{1}{2}\int\limits_{{x_0}}^x {\left( {{x^2}{\tau ^2} - 2x{\tau ^3} + {\tau ^4} - {x^2} + 2x\tau - {\tau ^2}} \right)d\tau } } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{{x^2}{\tau ^3}}}{3} - \frac{{x{\tau ^4}}}{4} + \frac{{{\tau ^5}}}{5} - {x^2}\tau + x{\tau ^2} - \frac{{{\tau ^3}}}{3}} \right)} \right|_{\tau = {x_0}}^{\tau = x}} \right] } = {\frac{1}{2}\left( {\frac{{{x^5}}}{3} - \frac{{{x^5}}}{2} + \frac{{{x^5}}}{5} - \cancel{x^3} + \cancel{x^3} - \frac{{{x^3}}}{3} + \alpha {x^2} + \beta x + \gamma } \right),} \] где \(\alpha,\) \(\beta,\) \(\gamma\) обозначают коэффициенты, зависящие от \({x_0}.\)

Тогда общее решение уравнения представляется в виде: \[ {y\left( x \right) = \frac{1}{2}\left[ {\left( {\frac{1}{3} - \frac{1}{2} + \frac{1}{5}} \right){x^5} - \frac{{{x^3}}}{3} + \alpha {x^2} + \beta x + \gamma } \right] } + {{C_1}\frac{{{{\left( {x - {x_0}} \right)}^2}}}{2} } + {{C_2}\left( {x - {x_0}} \right) + {C_3}.} \] Учитывая, что числа \({C_1}\) и \({x_0}\) произвольные, общее решение \(y\left( x \right)\) можно переписать в виде: \[y\left( x \right) = \frac{{{x^5}}}{{60}} - \frac{{{x^3}}}{6} + {C_1}{x^2} + {C_2}x + {C_3}.\] Примечание: Такой же ответ получается последовательным интегрированием заданного дифференциального уравнения.

   Пример 2

Найти частное решение уравнения \({y^{IV}} = \sin x + 1\) при начальных условиях \({x_0} = 0,\) \({y_0} = 1,\) \({y'_0} = {y''_0} = {y'''_0} = 0.\)
Построим сначала общее решение, последовательно интегрируя заданное уравнение: \[y''' = - \cos x + x + {C_1},\] \[y'' = - \sin x + \frac{{{x^2}}}{2} + {C_1}x + {C_2},\] \[y' = \cos x + \frac{{{x^3}}}{6} + \frac{{{C_1}{x^2}}}{2} + {C_2}x + {C_3},\] \[ {y = \sin x + \frac{{{x^4}}}{{24}} + \frac{{{C_1}{x^3}}}{6} } + {\frac{{{C_2}{x^2}}}{2} } + {{C_3}x + {C_4}.} \] Подставляя начальные значения, определим коэффициенты \({C_1} - {C_4}\) из системы уравнений: \[ {\left\{ \begin{array}{l} 0 = - 1 + {C_1}\\ 0 = {C_2}\\ 0 = 1 + {C_3}\\ 1 = {C_4} \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {C_1} = 0\\ {C_2} = 0\\ {C_3} = - 1\\ {C_4} = 1 \end{array} \right..} \] Следовательно, частное решение, удовлетворяющее начальным условиям, имеет вид: \[y\left( x \right) = \sin x + \frac{{{x^4}}}{{24}} + \frac{{{x^3}}}{6} - x + 1.\]

   Пример 3

Найти общее решение уравнения \({\left( {y''} \right)^2} - {\left( {y''} \right)^3} = x.\)
Данное уравнение можно решить параметрическим методом. Полагаем \(y'' = t.\) Тогда \[x = {t^2} - {t^3}.\] Учитывая, что \(d\left( {y'} \right) = y''dx,\) находим производную \(y',\) выраженную через параметр \(t:\) \[ {d\left( {y'} \right) = y''dx = t\left( {2t - 3{t^2}} \right)dt = \left( {2{t^2} - 3{t^3}} \right)dt,}\;\; {\Rightarrow y' = \int {\left( {2{t^2} - 3{t^3}} \right)dt} = \frac{{2{t^3}}}{3} - \frac{{3{t^4}}}{4} + {C_1}.} \] Аналогично выполняем еще одно интегрирование: \[ {dy = y'dx = \left( {\frac{{2{t^3}}}{3} - \frac{{3{t^4}}}{4} + {C_1}} \right)\left( {2t - 3{t^2}} \right)dt } = {\left( {\frac{{4{t^3}}}{3} - \frac{{3{t^4}}}{2} + 2{C_1}t - {t^5} + \frac{{9{t^6}}}{4} - 3{C_1}{t^2}} \right)dt,} \] \[ {\Rightarrow y = \int {\left( {\frac{{4{t^3}}}{3} - \frac{{3{t^4}}}{2} + 2{C_1}t - {t^5} + \frac{{9{t^6}}}{4} - 3{C_1}{t^2}} \right)dt} } = {\frac{{{t^4}}}{3} - \frac{{3{t^5}}}{{10}} + {C_1}{t^2} - \frac{{{t^6}}}{6} + \frac{{9{t^7}}}{{28}} - {C_1}{t^3} + {C_2} } = {\frac{{9{t^7}}}{{28}} - \frac{{{t^6}}}{6} - \frac{{3{t^5}}}{{10}} + \frac{{{t^4}}}{3} - {C_1}{t^3} + {C_1}{t^2} + {C_2}.} \] Таким образом, общее решение представляется в параметрической форме как \[\left\{ \begin{array}{l} x = {t^2} - {t^3}\\ y = \frac{{9{t^7}}}{{28}} - \frac{{{t^6}}}{6} - \frac{{3{t^5}}}{{10}} + \frac{{{t^4}}}{3} - {C_1}{t^3} + {C_1}{t^2} + {C_2} \end{array} \right.,\] где \({C_1},\) \({C_2}\) − произвольные постоянные.

   Пример 4

Найти частное решение уравнения \({y^{IV}} - y''' = 1\) при нулевых начальных условиях: \({x_0} = 0,\) \({y_0} = {y'_0} = {y''_0} = {y'''_0} = 0.\)
Данное уравнение относится к типу \(2.\) Введем промежуточную переменную \(z = y'''.\) Получаем линейное уравнение первого порядка: \[z' - z = 1.\] Его общим решением является функция \[z = {C_1}{e^x} - 1.\] Следовательно, имеем \[y''' = {C_1}{e^x} - 1,\] т.е. уравнение преобразовано к типу \(1.\) Его можно решить последовательным интегрированием: \[y'' = {C_1}{e^x} - x + {C_2},\] \[y' = {C_1}{e^x} - \frac{{{x^2}}}{2} + {C_2}x + {C_3},\] \[y = {C_1}{e^x} - \frac{{{x^3}}}{6} + \frac{{{C_2}{x^2}}}{2} + {C_3}x + {C_4}.\] Коэффициенты \({C_i}\) определяются из начальных условий: \[\left\{ \begin{array}{l} 0 = {C_1} - 1\\ 0 = {C_1} + {C_2}\\ 0 = {C_1} + {C_3}\\ 0 = {C_1} + {C_4} \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} {C_1} = 1\\ {C_2} = - 1\\ {C_3} = - 1\\ {C_4} = - 1 \end{array} \right..\] Итак, частное решение при заданных начальных условиях имеет вид: \[y\left( x \right) = {e^x} - \frac{{{x^3}}}{6} - \frac{{{x^2}}}{2} - x - 1.\]

   Пример 5

Найти общее решение дифференциального уравнения \(y''' = \sqrt {1 - {{\left( {y''} \right)}^2}} .\)
Данное уравнение относится к типу \(2.\) Вводим новую переменную \(z = y''.\) Получаем уравнение первого порядка: \[z' = \sqrt {1 - {z^2}} .\] Будем полагать, что функция \(z\) задана на отрезке \(\left[ { - 1,1} \right].\) Интегрируя, находим: \[ {\frac{{dz}}{{dx}} = \sqrt {1 - {z^2}} ,}\;\; {\Rightarrow \frac{{dz}}{{\sqrt {1 - {z^2}} }} = dx,}\;\; {\Rightarrow \int {\frac{{dz}}{{\sqrt {1 - {z^2}} }}} = \int {dx} ,}\;\; {\Rightarrow \arcsin z = x + {C_1},}\;\; {\Rightarrow z = \sin \left( {x + {C_1}} \right).} \] Фактически мы привели исходное уравнение к типу \(1.\) Общее решение \(y\left( x \right)\) проще всего получить, дважды интегрируя выражение для \(z:\) \[y'' = \sin \left( {x + {C_1}} \right),\] \[y' = - \cos \left( {x + {C_1}} \right) + {C_2},\] \[y = - \sin \left( {x + {C_1}} \right) + {C_2}x + {C_3},\] где \({C_1},{C_2},{C_3}\) − произвольные постоянные.

   Пример 6

Построить общее решение уравнения \(y'''y'' = 1\) в квадратурах.
Это уравнение типа \(3.\) Вводим новую функцию \(z = y',\) так что уравнение будет записываться в виде \[z''z = 1,\;\; \Rightarrow z'' = \frac{1}{z}.\] Очевидно, что \(z = y' \ne 0\) и \(z' = y'' \ne 0.\) Умножим обе части полученного уравнения на \(2z'\) и проинтегрируем один раз: \[ {2z'z'' = \frac{{2z'}}{z},}\;\; {\Rightarrow d{\left( {z'} \right)^2} = \frac{{2dz}}{z},}\;\; {\Rightarrow {\left( {z'} \right)^2} = 2\ln \left| z \right| + \ln {C_1} = \ln \left( {{C_1}{z^2}} \right).} \] Видно, что уравнение приведено к типу \(1.\) Далее его удобно решать параметрическим методом. Положим \(z' = t,\) где переменная \(t\) рассматривается как параметр. Функция \(z\) выражается через \(t\) следующим образом: \[ {{t^2} = \ln \left( {{C_1}{z^2}} \right),}\;\; {\Rightarrow {C_1}{z^2} = {e^{{t^2}}},}\;\; {\Rightarrow z = \pm \frac{1}{{{C_1}}}{e^{{t^2}}}.} \] Таким образом, функция \(z\) представлена в виде \(z = \varphi \left( {t,{C_1}} \right).\) Зависимость переменной \(x\) от параметра \(t\) также описывается квадратурой: \[ {t = z' = \frac{{dz}}{{dx}},}\;\; {\Rightarrow dx = \frac{{dz}}{t} = \frac{{\varphi '\left( {t,{C_1}} \right)dt}}{t},}\;\; {\Rightarrow x = \int {\frac{{\varphi '\left( {t,{C_1}} \right)dt}}{t}} + {C_2}.} \] Остается получить параметрическое выражение для функции \(y.\) Поскольку \[ {z = \frac{{dy}}{{dx}},}\;\; {\Rightarrow dy = zdx = \frac{{\varphi \left( {t,{C_1}} \right)\varphi '\left( {t,{C_1}} \right)dt}}{t},} \] то после интегрирования имеем: \[y = \int {\frac{{\varphi \left( {t,{C_1}} \right)\varphi '\left( {t,{C_1}} \right)}}{t}dt} + {C_3}.\] Итак, общее решение исходного уравнения в параметрической форме выражается через квадратуры в следующем виде: \[ {x = \int {\frac{{\varphi '\left( {t,{C_1}} \right)}}{t}dt} + {C_2},}\;\;\; {y = \int {\frac{{\varphi \left( {t,{C_1}} \right)\varphi '\left( {t,{C_1}} \right)}}{t}dt} + {C_3}.} \] где \(\varphi \left( {t,{C_1}} \right) = \pm {\large\frac{1}{{{C_1}}}\normalsize}{e^{{t^2}}}\) и \({C_1},{C_2},{C_3}\) − постоянные интегрирования.