Уравнения касательной и нормали

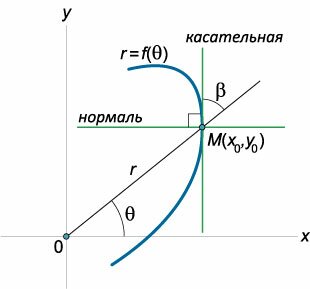
Предположим, что функция \(y = f\left( x \right)\) определена на интервале \(\left( {a,b} \right)\) и непрерывна в точке \({x_0} \in \left( {a,b} \right).\) В этой точке (точка \(M\) на рисунке \(1\)) функция имеет значение \({y_0} = f\left( {{x_0}} \right).\)

Пусть независимая переменная в точке \({x_0}\) получает приращение \(\Delta x.\) Соответствующее приращение функции \(\Delta y\) выражается формулой \[\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right).\] На рисунке \(1\) точка \({M_1}\) имеет координаты \(\left( {{x_0} + \Delta x,{y_0} + \Delta y} \right).\) Построим секущую \(M{M_1}.\) Ее уравнение имеет вид \[y - {y_0} = k\left( {x - {x_0}} \right),\] где \(k\) − угловой коэффициент, зависящий от приращения \(\Delta x\) и равный \[k = k\left( {\Delta x} \right) = \frac{{\Delta y}}{{\Delta x}}.\] При уменьшении \(\Delta x\) точка \({M_1}\) стремится к точке \(M:\) \({M_1} \to M.\) В пределе \(\Delta x \to 0\) расстояние между точками \(M\) и \({M_1}\) стремится к нулю. Это следует из непрерывности функции \(f\left( x \right)\) в точке \({x_0}:\) \[ {\lim\limits_{\Delta x \to 0} \Delta y = 0,}\;\; {\Rightarrow \lim\limits_{\Delta x \to 0} \left| {M{M_1}} \right| } = {\lim\limits_{\Delta x \to 0} \sqrt {{{\left( {\Delta x} \right)}^2} + {{\left( {\Delta y} \right)}^2}} = 0.} \] Предельное положение секущей \(M{M_1}\) как раз и представляет собой касательную прямую к графику функции \(y = f\left( x \right)\) в точке \(M.\)

Возможны два вида касательных − наклонные и вертикальные.

Определение \(1\).
Если существует конечный предел \(\lim\limits_{\Delta x \to 0} k\left( {\Delta x} \right) = {k_0},\) то прямая, имеющая уравнение \[y - {y_0} = k\left( {x - {x_0}} \right),\] называется наклонной касательной к графику функции \(y = f\left( x \right)\) в точке \(\left( {{x_0},{y_0}} \right).\)

Определение 2.
Если предельное значение \(k\) при \(\Delta x \to 0\) является бесконечным: \(\lim\limits_{\Delta x \to 0} k\left( {\Delta x} \right) = \pm \infty,\) то прямая, имеющая уравнение \[x = {x_0},\] называется вертикальной касательной к графику функции \(y = f\left( x \right)\) в точке \(\left( {{x_0},{y_0}} \right).\)

Важно отметить, что \[ {{k_0} = \lim\limits_{\Delta x \to 0} k\left( {\Delta x} \right) } = {\lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} } = {f'\left( {{x_0}} \right),} \] то есть угловой коэффициент касательной равен значению производной функции \(f\left( {{x_0}} \right)\) в точке касания \({x_0}.\) Поэтому уравнение наклонной касательной можно записать в таком виде: \[ {y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\;\;\text{или}}\;\; {y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right).} \] Поскольку угловой коэффициент прямой равен тангенсу угла наклона \(\alpha,\) который прямая образует с положительным направлением оси абсцисс, то справедливо следующее тройное равенство: \[k = \tan \alpha = f'\left( {{x_0}} \right).\] Прямая, перпендикулярная касательной и проходящая через точку касания \(\left( {{x_0},{y_0}} \right),\) называется нормалью к графику функции \(y = f\left( x \right)\) в этой точке (рисунок \(2\)).

Из геометрии известно, что произведение угловых коэффициентов перпендикулярных прямых равно \(-1.\) Поэтому, зная уравнение касательной в точке \(\left( {{x_0},{y_0}} \right):\) \[y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right),\] можно сразу записать уравнение нормали в виде \[y - {y_0} = - \frac{1}{{f'\left( {{x_0}} \right)}}\left( {x - {x_0}} \right).\] Пусть плоская кривая задана параметрически: \[x = x\left( t \right),\;\;\;y = y\left( t \right).\] Тогда угловой коэффициент касательной, проведенной в точке \(\left( {{x_0},{y_0}} \right),\) находится по правилу дифференцирования параметрически заданной кривой: \[k = \tan \alpha = \frac{{{y'_t}}}{{{x'_t}}}.\] Уравнение касательной имеет вид \[ {y - {y_0} = \frac{{{y'_t}}}{{{x'_t}}}\left( {x - {x_0}} \right)}\;\;\; {\text{или}\;\;\;\frac{{x - {x_0}}}{{{x'_t}}} = \frac{{y - {y_0}}}{{{y'_t}}}.} \] Соответственно, уравнение нормали записывается как \[ {y - {y_0} = - \frac{{{x'_t}}}{{{y'_t}}}\left( {x - {x_0}} \right)}\;\;\; {\text{или}\;\;\;\frac{{x - {x_0}}}{{{y'_t}}} = - \frac{{y - {y_0}}}{{{x'_t}}}.} \] Предположим, что кривая задана полярным уравнением \(r = f\left( \theta \right),\) выражающим зависимость длины радиуса-вектора \(r\) от полярного угла \(\theta.\) В декартовых координатах такая кривая будет описываться системой уравнений \[\left\{ \begin{array}{l} x = r\cos \theta = f\left( \theta \right)\cos \theta \\ y = r\sin \theta = f\left( \theta \right)\sin\theta \end{array} \right..\] Таким образом, мы записали уравнение кривой в параметрической форме, где роль параметра играет угол \(\theta.\) Далее легко получить выражение для углового коэффициента касательной, проведенной к кривой в точке \(\left( {{x_0},{y_0}} \right):\) \[ {k = \tan \theta = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{{{\left( {r\sin \theta } \right)}^\prime }}}{{{{\left( {r\cos \theta } \right)}^\prime }}} } = {\frac{{{r'_\theta }\sin \theta + r\cos \theta }}{{{r'_\theta }\cos\theta - r\sin \theta }}.} \] В результате уравнения касательной и нормали будут записываться в следующем виде: \[ {y - {y_0} = \frac{{{y'_\theta }}}{{{x'_\theta }}}\left( {x - {x_0}} \right)}\;\;\; {(\text{касательная}),} \] \[ {y - {y_0} = -\frac{{{x'_\theta }}}{{{y'_\theta }}}\left( {x - {x_0}} \right)}\;\;\; {(\text{нормаль}).} \] Исследование кривой можно провести непосредственно в полярных координатах без перехода к декартовой системе. В таком случае наклон касательной удобно определять не углом \(\theta\) с полярной осью (т.е. с положительным направлением оси абсцисс), а углом \(\beta\) с прямой, содержащей радиус-вектор \(r\) (рисунок \(3\)).

Тангенс угла \(\beta\) вычисляется по формуле \[\tan \beta = \frac{r}{{{r'_\theta }}}.\] Угол, образованный нормалью с продолженным радиусом-вектором, равен \(\beta + \large\frac{\pi }{2}\normalsize.\) По формуле приведения получаем: \[ {\tan \left( {\beta + \frac{\pi }{2}} \right) } = { - \cot \beta = - \frac{1}{{\tan \beta }} } = { - \frac{{{r'_\theta }}}{r}.} \]

   Пример 1

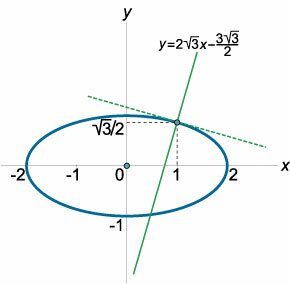
Написать уравнение нормали к эллипсу \[\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\] в точке \(\left( {1,\large\frac{{\sqrt 3 }}{2}\normalsize} \right)\) (рисунок \(4\)). Найдем производную \(y'\left( x \right),\) дифференцируя функцию неявно: \[ {{\left( {\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1}} \right)^\prime } = 1',}\;\; {\Rightarrow \frac{{2x}}{4} + 2yy' = 0,}\;\; {\Rightarrow 4yy' = - x,}\;\; {\Rightarrow y = - \frac{x}{{4y}}.} \] В точке касания производная равна \[ {y'\left( {{x_0},{y_0}} \right) = y'\left( {1,\frac{{\sqrt 3 }}{2}} \right) } = { - \frac{1}{{\frac{{4\sqrt 3 }}{2}}} } = { - \frac{1}{{2\sqrt 3 }}.} \] Тогда уравнение нормали записывается в виде \[ {y - {y_0} = - \frac{1}{{y'\left( {{x_0},{y_0}} \right)}}\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - \frac{{\sqrt 3 }}{2} = - \frac{1}{{\left( { - \frac{1}{{2\sqrt 3 }}} \right)}}\left( {x - 1} \right),}\;\; {\Rightarrow y - \frac{{\sqrt 3 }}{2} = 2\sqrt 3 x - 2\sqrt 3 ,}\;\; {\Rightarrow y = 2\sqrt 3 x - 2\sqrt 3 + \frac{{\sqrt 3 }}{2},}\;\; {\Rightarrow y = 2\sqrt 3 x - \frac{{3\sqrt 3 }}{2} \approx 3,46x - 2,60.} \]

   Пример 2

Под какими углами кривая \(y = {x^3} - x\) пересекает ось абсцисс? Кубическая функция \(y = {x^3} - x\) пересекает ось абсцисс в следующих точках: \[ {f\left( x \right) = 0,}\;\; {\Rightarrow {x^3} - x = 0,}\;\; {\Rightarrow x\left( {x - 1} \right)\left( {x + 1} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_{2,3}} = \pm 1.} \] Вычислим значения производной в этих точках: \[ {f'\left( x \right) = {\left( {{x^3} - x} \right)^\prime } } = {3{x^2} - 1;} \] \[ {f'\left( 0 \right) = 3 \cdot {0^2} - 1 = - 1,}\;\;\; {f'\left( { - 1} \right) = 3 \cdot {\left( { - 1} \right)^2} - 1 = 2,}\;\;\; {f'\left( 1 \right) = 3 \cdot {1^2} - 1 = 2.} \] Угол, под которым кривая пересекает ось \(Ox,\) определяется углом наклона касательной, проведенной к графику функции в точке пересечения. В свою очередь, тангенс угла наклона касательной равен значению производной в точке касания. Следовательно, получаем следующие значения углов в точках пересечения:

1. \({x_1} = 0,\;\; {\Rightarrow f'\left( 0 \right) = - 1,}\;\; {\Rightarrow \tan {\alpha _1} = - 1,}\;\; {\Rightarrow {\alpha _1} = \large\frac{{3\pi }}{4}\normalsize = 135^{\circ};} \)

2. \({x_2} = - 1,\;\; {\Rightarrow f'\left( { - 1} \right) = 2,}\;\; {\Rightarrow \tan {\alpha _2} = 2,}\;\; {\Rightarrow {\alpha _2} = \arctan 2 \approx 63^{\circ};} \)

3. \({x_3} = 1,\;\; {\Rightarrow f'\left( {1} \right) = 2,}\;\; {\Rightarrow \tan {\alpha _3} = 2,}\;\; {\Rightarrow {\alpha _3} = \arctan 2 \approx 63^{\circ}.} \)

   Пример 3

Написать уравнения касательной и нормали к графику функции \(y = x\sqrt {x - 1} \) в точке \(x = 2.\) Вычислим производную заданной функции: \[ {y'\left( x \right) = {\left( {x\sqrt {x - 1} } \right)^\prime } } = {x'\sqrt {x - 1} + x{\left( {\sqrt {x - 1} } \right)^\prime } } = {\sqrt {x - 1} + \frac{x}{{2\sqrt {x - 1} }} } = {\frac{{2\left( {x - 1} \right) + x}}{{2\sqrt {x - 1} }} } = {\frac{{3x - 2}}{{2\sqrt {x - 1} }}.} \] В точке \(x = 2\) производная равна \[y'\left( 2 \right) = \frac{{3 \cdot 2 - 2}}{{2\sqrt {2 - 1} }} = 2.\] Значение самой функции в этой точке составляет \[y\left( 2 \right) = 2 \cdot 1 = 2.\] Находим уравнение касательной: \[ {y - {y_0} = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - 2 = 2\left( {x - 2} \right),}\;\; {\Rightarrow y - 2 = 2x - 4,}\;\; {\Rightarrow y = 2x - 2.} \] и уравнение нормали в этой же точке: \[ {y - {y_0} = - \frac{1}{{y'\left( {{x_0}} \right)}}\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - 2 = - \frac{1}{2}\left( {x - 2} \right),}\;\; {\Rightarrow y - 2 = - \frac{x}{2} + 1,}\;\; {\Rightarrow y = - \frac{x}{2} + 3.} \]

   Пример 4

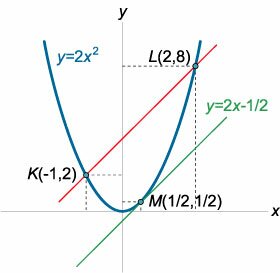
Дана парабола \(y = 2{x^2}.\) Через точки параболы с координатами \(x = -1\) и \(x = 2\) проведена секущая (рисунок \(5\)). Найти касательную к параболе, параллельную данной секущей. Вычислим сначала координаты \(y\) хорды \(KL\) (рисунок \(5\)): \[ {y\left( { - 1} \right) = 2 \cdot {\left( { - 1} \right)^2} = 2;}\;\;\; {y\left( 2 \right) = 2 \cdot {2^2} = 8.} \] Тогда уравнение секущей \(KL\) записывается в виде \[ {\frac{{y - {y_K}}}{{{y_L} - {y_K}}} = \frac{{x - {x_K}}}{{{x_L} - {x_K}}},}\;\; {\Rightarrow \frac{{y - 2}}{{8 - 2}} = \frac{{x - \left( { - 1} \right)}}{{2 - \left( { - 1} \right)}},}\;\; {\Rightarrow \frac{{y - 2}}{6} = \frac{{x + 1}}{3},}\;\; {\Rightarrow y - 2 = 2\left( {x + 1} \right),}\;\; {\Rightarrow y = 2x + 4.} \] то есть, \(k = 2.\) Угловой коэффициент касательной имеет такое же значение \(k = 2.\)

Найдем координаты точки касания из условия \(y'\left( x \right) = k:\) \[ {y'\left( x \right) = k,}\;\; {\Rightarrow {\left( {2{x^2}} \right)^\prime } = 2,}\;\; {\Rightarrow 4x = 2,}\;\; {\Rightarrow x = \frac{1}{2}.} \] Следовательно, координата \(y\) точки касания \(M\) равна \[{y_M} = 2 \cdot {\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}.\] Таким образом, точка касания \(M\) имеет координаты \(\left( {\large\frac{1}{2}\normalsize,\large\frac{1}{2}\normalsize} \right).\) Отсюда получаем уравнение искомой касательной в следующем виде: \[ {y - {y_M} = k\left( {x - {x_M}} \right),}\;\; {\Rightarrow y - \frac{1}{2} = 2\left( {x - \frac{1}{2}} \right),}\;\; {\Rightarrow y - \frac{1}{2} = 2x - 1,}\;\; {\Rightarrow y = 2x - \frac{1}{2}.} \]

   Пример 5

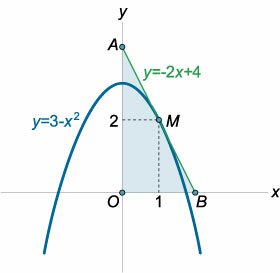
Определить площадь треугольника, образованного касательной к графику функции \(y = 3 - {x^2},\) проведенной в точке \(\left( {1,2} \right),\) и осями координат (рисунок \(6\)). Найдем уравнение касательной. Учитывая, что \[ {f'\left( x \right) = \left( {3 - {x^2}} \right) = - 2x;}\;\; {\Rightarrow f'\left( 1 \right) = - 2,} \] получаем уравнение касательной в следующем виде: \[ {y - {y_M} = f'\left( {{x_M}} \right)\left( {x - {x_M}} \right),}\;\; {\Rightarrow y - 2 = - 2\left( {x - 1} \right),}\;\; {\Rightarrow y = - 2x + 4.} \] Приведем его в форму уравнения в отрезках: \[ {y = - 2x + 4,}\;\; {\Rightarrow y + 2x = 4,}\;\; {\Rightarrow \frac{y}{4} + \frac{{2x}}{4} = 1,}\;\; {\Rightarrow \frac{y}{4} + \frac{x}{2} = 1.} \] Отсюда следует, что длина отрезка \(OA\) составляет \(4,\) а длина отрезка \(OB\) равна \(2.\) Площадь треугольника \(OAB,\) соответственно, равна \[S = \frac{{\left| {OA} \right| \cdot \left| {OB} \right|}}{2} = \frac{{4 \cdot 2}}{2} = 4.\]

   Пример 6

Парабола задана уравнением \(y = {x^2} + 2x + 3.\) Составить уравнения касательных к параболе, проходящих через точку \(A\left( { - 1,1} \right).\) Преобразуем уравнение параболы к виду \[ {y = {x^2} + 2x + 3 } = {{x^2} + 2x + 1 + 2 } = {{\left( {x + 1} \right)^2} + 2.} \] Видно, что график данной параболы получается из графика функции \(y = {x^2}\) в результате параллельного переноса на \(1\) единицу влево и на \(2\) единицы вверх (рисунок \(7\)).

Найдем уравнения двух касательных к параболе, проходящих через точку \(A\left( { - 1,1} \right).\) Каждая из этих касательных определяется уравнением \[ {y - {y_A} = k\left( {x - {x_A}} \right),}\;\; {\Rightarrow y - 1 = k\left( {x - \left( { - 1} \right)} \right),}\;\; {\Rightarrow y - 1 = kx + k,}\;\; {\Rightarrow y = kx + k + 1,} \] где \(k\) − угловой коэффициент (\({k_1}\) − для первой касательной и \({k_2}\) − для второй).

Таким образом, задача сводится к определению угловых коэффициентов касательных \({k_1}\) и \({k_2}.\) Учтем, что в точках касания \(B\) и \(C\) выполняется условие \[ {\left\{ \begin{array}{l} y = kx + k + 1\\ y = {x^2} + 2x + 3 \end{array} \right.,}\;\; {\Rightarrow kx + k + 1 = {x^2} + 2x + 3.} \] Кроме того, в точках касания \(B\) и \(C\) угловой коэффициент равен значению производной функции \(y = {x^2} + 2x + 3.\) Поскольку \[ {y' = {\left( {{x^2} + 2x + 3} \right)^\prime } } = {2x + 2,} \] то, следовательно, получаем еще одно уравнение в виде \[k = 2x + 2.\] В результате мы имеем систему двух уравнений \[\left\{ \begin{array}{l} kx + k + 1 = {x^2} + 2x + 3\\ k = 2x + 2 \end{array} \right.\] с двумя неизвестными \(k\) и \(x.\) Решая эту систему, находим значения \(k\) и \(x\) (т.е. угловые коэффициенты касательных \({k_1},\) \({k_2}\) и абсциссы точек касания \(B\) и \(C\)): \[ {\left\{ \begin{array}{l} kx + k + 1 = {x^2} + 2x + 3\\ k = 2x + 2 \end{array} \right.,}\;\; {\Rightarrow \left( {2x + 2} \right)x + 2x + 2 + 1 = {x^2} + 2x + 3,}\;\; {\Rightarrow 2{x^2} + 2x + 2x + 3 = {x^2} + 2x + 3,}\;\; {\Rightarrow {x^2} + 2x = 0,}\;\; {\Rightarrow {x_1} = - 2,\;{x_2} = 0.} \] Первое решение \({x_1} = - 2\) соответствует точке \(B.\) Второе решение \({x_2} = 0\) является координатой точки касания \(C.\) Угловые коэффициенты имеют следующие значения:

1. касательная \(AB:\;\) \({x_1} = -2,\) \({k_1} = -2;\)

2. касательная \(AC:\;\) \({x_2} = 0,\) \({k_2} = 2.\)

Тогда уравнения касательных к данной параболе записываются в виде

1. касательная \(AB:\;\) \(y = -2x - 1;\)

2. касательная \(AC:\;\) \(y = 2x + 3.\)

   Пример 7

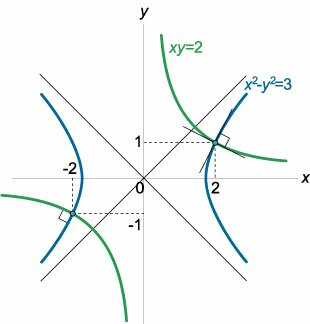
Доказать, что кривые \({x^2} - {y^2} = 3\) и \(xy = 2\) пересекаются под прямым углом. Данные кривые представляют собой гиперболы и схематически изображены на рисунке \(8.\) Определим их точки пересечения: \[ {\left\{ \begin{array}{l} {x^2} - {y^2} = 3\\ xy = 2 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {x^2} - {y^2} = 3\\ y = \frac{2}{x} \end{array} \right.,}\;\; {\Rightarrow {x^2} - {\left( {\frac{2}{x}} \right)^2} = 3,}\;\; {\Rightarrow \frac{{{x^2} - 4}}{{{x^2}}} = 3,}\;\; {\Rightarrow {x^4} - 3{x^2} - 4 = 0,}\;\; {\Rightarrow D = 9 + 16 = 25,}\;\; {\Rightarrow {x^2} = \frac{{3 \pm 5}}{2} = - 1;\;4.} \] Очевидно, что точки пересечения кривых находятся из условия \({x^2} = 4:\) \[{x^2} = 4,\;\; \Rightarrow {x_{1,2}} = \pm 2.\] Вычислим координаты \(y\) данных точек: \[ {{x_1} = - 2,}\;\; {\Rightarrow {y_1} = \frac{2}{{\left( { - 2} \right)}} = - 1;} \] \[ {{x_2} = 2,}\;\; {\Rightarrow {y_2} = \frac{2}{2} = 1.} \] Найдем теперь производные заданных функций. Производную первой функции вычислим с помощью неявного дифференцирования: \[ {{x^2} - {y^2} = 3,}\;\; {\Rightarrow {\left( {{x^2} - {y^2}} \right)^\prime } = 3',}\;\; {\Rightarrow 2x - 2yy' = 0,}\;\; {\Rightarrow y' = \frac{x}{y}.} \] Производная второй функции выражается в виде \[y' = {\left( {\frac{2}{x}} \right)^\prime } = - \frac{2}{{{x^2}}}.\] Вычислим значения производных в точке \(x = -2\) (тем самым мы найдем угловые коэффициенты касательных к каждой гиперболе в этой точке) и убедимся, что произведение угловых коэффициентов касательных в данной точке равно \(-1:\) \[\require{AMSmath.js} {{k_1} = {\left( {\frac{x}{y}} \right)_{\substack{ x = -2\\ y= -1}}} = \frac{{\left( { - 2} \right)}}{{\left( { - 1} \right)}} = 2;}\;\; {{k_2} = {\left( { - \frac{2}{{{x^2}}}} \right)_{x = - 2}} = - \frac{1}{2};}\;\; {\Rightarrow {k_1}{k_2} = 2 \cdot \left( { - \frac{1}{2}} \right) = - 1.} \] Такую же проверку сделаем для второй точки пересечения: \[ {{k_1} = {\left( {\frac{x}{y}} \right)_{\substack{ x = 2\\ y= 1}}} = \frac{{2}}{{1}} = 2;}\;\; {{k_2} = {\left( { - \frac{2}{{{x^2}}}} \right)_{x = 2}} = - \frac{1}{2};}\;\; {\Rightarrow {k_1}{k_2} = 2 \cdot \left( { - \frac{1}{2}} \right) = - 1.} \] Таким образом в каждой из двух точек кривые пересекаются под прямым углом.

   Пример 8

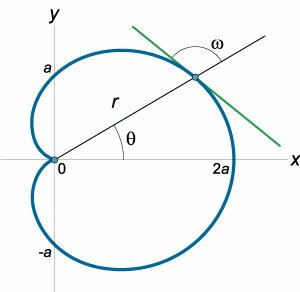
Найти угол между касательной к кардиоиде \(r = a\left( {1 + \cos \theta } \right)\) и радиусом-вектором точки касания. Искомый угол (рисунок \(9\)) вычисляется по формуле \[\tan \omega = \frac{r}{{{r'_\theta }}}.\] Здесь \[ {{r'_\theta } = {\left[ {a\left( {1 + \cos \theta } \right)} \right]^\prime } } = { - a\sin \theta .} \] Следовательно, \[\require{cancel} {\tan \omega = \frac{{a\left( {1 + \cos \theta } \right)}}{{\left( { - a\sin \theta } \right)}} } = { - \frac{{1 + \cos \theta }}{{\sin\theta }} } = { - \frac{{\cancel{2}{{\cos }^{\cancel{2}}}\frac{\theta }{2}}}{{\cancel{2}\sin \frac{\theta }{2}\cancel{\cos \frac{\theta }{2}}}} } = { - \cot \frac{\theta }{2} } = {\tan \left( {\frac{\theta }{2} + \frac{\pi }{2}} \right).} \] В последнем выражении мы воспользовались формулой приведения. Таким образом, угол между касательной и радиусом-вектором равен \[\omega = \frac{\theta }{2} + \frac{\pi }{2}.\]

   Пример 9

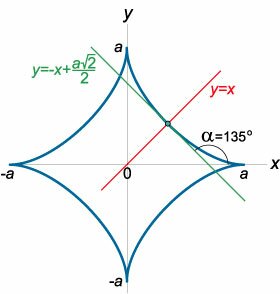
Найти уравнение касательной и нормали к астроиде \(x = a\,{\cos ^3}t,\) \(y = a\,{\sin ^3}t\) в точке \(t = \large\frac{\pi }{4}\normalsize\) (рисунок \(10\)). Вычислим производные параметрически заданной функции: \[ {{x'_t} = {\left( {a\,{{\cos }^3}t} \right)^\prime } = - 3a\,{\cos ^2}t\sin t;}\;\;\; {{y'_t} = {\left( {a\,{{\sin }^3}t} \right)^\prime } = 3a\,{\sin ^2}t\cos t.} \] Следовательно, \[ {{y'_x} = \frac{{{y'_t}}}{{{x'_t}}} } = {\frac{{3a\,{{\sin }^2}t\cos t}}{{\left( { - 3a\,{{\cos }^2}t\sin t} \right)}} } = { - \frac{{\sin t}}{{\cos t}} } = { - \tan t.} \] По формуле приведения можно записать: \[ - \tan t = \tan \left( {\pi - t} \right).\] Так как \(\tan \alpha = {y'_x} = \tan \left( {\pi - t} \right),\) то угол \(\alpha\) составляет \[ {\alpha = \pi - t } = {\pi - \frac{\pi }{4} } = {\frac{{3\pi }}{4} = 135^{\circ}.} \] Тогда производная кардиоиды и, соответственно, угловой коэффициент касательной в точке касания равны \[{y'_x}\left( {\frac{\pi }{4}} \right) = \tan \frac{{3\pi }}{4} = - 1.\] Находим координаты точки касания: \[ {{x_0} = x\left( {\frac{\pi }{4}} \right) } = {a\,{\cos ^3}\frac{\pi }{4} } = {a{\left( {\frac{{\sqrt 2 }}{2}} \right)^3} } = {\frac{{a\sqrt 2 }}{4},} \] \[ {{y_0} = y\left( {\frac{\pi }{4}} \right) } = {a\,{\sin ^3}\frac{\pi }{4} } = {a{\left( {\frac{{\sqrt 2 }}{2}} \right)^3} } = {\frac{{a\sqrt 2 }}{4}.} \] Теперь можно записать уравнение касательной: \[ {y - {y_0} = {y'_x}\left( {{x_0}} \right)\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - \frac{{a\sqrt 2 }}{4} = - 1\left( {x - \frac{{a\sqrt 2 }}{4}} \right),}\;\; {\Rightarrow y - \frac{{a\sqrt 2 }}{4} = - x + \frac{{a\sqrt 2 }}{4},}\;\; {\Rightarrow y = - x + \frac{{a\sqrt 2 }}{2}} \] и уравнение нормали: \[ {y - {y_0} = - \frac{1}{{{{y'}_x}\left( {{x_0}} \right)}}\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - \frac{{a\sqrt 2 }}{4} = - \frac{1}{{\left( { - 1} \right)}}\left( {x - \frac{{a\sqrt 2 }}{4}} \right),}\;\; {\Rightarrow y - \cancel{\frac{{a\sqrt 2 }}{4}} = x - \cancel{\frac{{a\sqrt 2 }}{4}},}\;\; {\Rightarrow y = x.} \]

   Пример 10

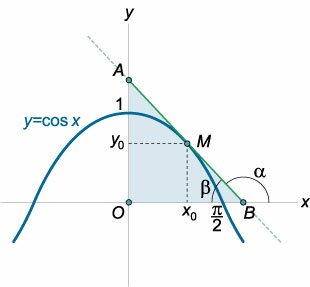
К графику функции \(y =\cos x\) проведена касательная в точке \(M\left( {{x_0},{y_0}} \right),\) где \(0 < {x_0} < \large\frac{\pi }{2}\normalsize\) (рисунок \(11\)). Найти значение \({x_0},\) при котором площадь треугольника, образованного касательной и осями координат, будет наименьшей. Поскольку производная косинуса равна \[y'\left( x \right) = {\left( {\cos x} \right)^\prime } = - \sin x,\] то угловой коэффициент касательной составляет \[\tan \alpha = - \sin {x_0} = y'\left( {{x_0}} \right).\] Тогда уравнение касательной имеет вид \[ {y - {y_0} = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - \cos {x_0} = - \sin {x_0}\left( {x - {x_0}} \right),}\;\; {\Rightarrow y - \cos {x_0} = \left( { - \sin {x_0}} \right)x - \left( { - \sin {x_0}} \right){x_0},}\;\; {\Rightarrow y + \left( {\sin {x_0}} \right)x = \cos {x_0} + \left( {\sin {x_0}} \right){x_0}.} \] Представим его в форме уравнения в отрезках: \[\frac{x}{p} + \frac{y}{q} = 1.\] Следовательно, \[ {\frac{y}{{\cos {x_0} + \left( {\sin {x_0}} \right){x_0}}} } {+ \frac{{\left( {\sin {x_0}} \right)x}}{{\cos {x_0} + \left( {\sin {x_0}} \right){x_0}}} = 1.} \] то есть, катеты прямоугольного треугольника \(OAB\) равны \[ {\left| {OA} \right| = q = \cos {x_0} + \left( {\sin {x_0}} \right){x_0},}\;\;\; {\left| {OB} \right| = p = \frac{{\cos {x_0} + \left( {\sin {x_0}} \right){x_0}}}{{\sin {x_0}}}.} \] Далее, для удобства, переобозначим \({x_0} = z.\) Выразим площадь треугольника \(OAB\) в виде функции \(S\left( z \right):\) \[ {S = S\left( z \right) = \frac{{pq}}{2} } = {\frac{{{{\left( {\cos z + z\sin z} \right)}^2}}}{{2\sin z}}.} \] Исследуем экстремальные значения функции \(S\left( z \right).\) Вычислим ее производную: \[ {S'\left( z \right) = \frac{1}{2}{\left[ {\frac{{{{\left( {\cos z + z\sin z} \right)}^2}}}{{\sin z}}} \right]^\prime } } = {\frac{1}{2} \cdot \frac{{2\left( {\cos z + z\sin z} \right)\left( { - \cancel{\sin z} + \cancel{\sin z} + z\cos z} \right)\sin z - {{\left( {\cos z + z\sin z} \right)}^2}\cos z}}{{{{\sin }^2}z}} } = {\frac{1}{2} \cdot \frac{{\left( {\cos z + z\sin z} \right)\left[ {2z\cos z\sin z - \left( {\cos z + z\sin z} \right)\cos z} \right]}}{{{{\sin }^2}z}} } = {\frac{1}{2} \cdot \frac{{\left( {\cos z + z\sin z} \right)\left[ {\color{blue}{2z\cos z\sin z} - {{\cos }^2}z - \color{blue}{z\cos z\sin z}} \right]}}{{{{\sin }^2}z}} } = {\frac{1}{2} \cdot \frac{{\left( {\cos z + z\sin z} \right)\left[ {\color{blue}{z\cos z\sin z} - {{\cos }^2}z} \right]}}{{{{\sin }^2}z}}.} \] Поскольку в интервале \(0 < z < \large\frac{\pi }{2}\normalsize\) \[\cos z + z\sin z > 0,\] то производная имеет лишь одну критическую точку, которая определяется условием \[ {z\cos z\sin z - {\cos ^2}z = 0,}\;\; {\Rightarrow \cos z\left( {z\sin z - \cos z} \right) = 0,}\;\; {\Rightarrow z - \cot z = 0.} \] Такое уравнение решается численно. Однако можно заметить, что если \(z = \large\frac{\pi }{4}\normalsize,\) то левая часть уравнения отрицательна: \[ {z = \frac{\pi }{4}:}\;\; {z - \cot z = \frac{\pi }{4} - \cot \frac{\pi }{4} } = {\frac{\pi }{4} - 1 \approx - 0,21 < 0.} \] а при \(z = \large\frac{\pi }{3}\normalsize\) левая часть положительна: \[ {z = \frac{\pi }{3}:}\;\; {z - \cot z = \frac{\pi }{3} - \cot \frac{\pi }{3} } = {\frac{\pi }{3} - \frac{1}{{\sqrt 3 }} \approx 0,47 > 0.} \] Следовательно, точка экстремума функции \(S\left( z \right)\) находится в интервале углов \(\left( {\large\frac{\pi }{4}\normalsize,\large\frac{\pi }{3}\normalsize} \right)\) (рисунок \(12\)), причем это точка является точкой минимума (судя по характеру изменения знака производной).

Приближенную координату точки минимума можно вычислить, например, в Excel. Она составляет примерно \(0.86\;\text{рад}\) или \(49,3^{\circ}.\)