Дифференциальное уравнение Чебышева

Дифференциальное уравнение вида \[\left( {1 - {x^2}} \right)y'' - xy' + {n^2}y = 0,\] где \(\left| x \right| < 1,\) а \(n\) − действительное число, называется уравнением Чебышева в честь знаменитого российского математика Пафнутия Чебышева.

Это уравнение можно преобразовать в более простую форму с помощью подстановки \(x = \cos t.\) Действительно, в этом случае мы получаем: \[ {x = \cos t,\;\; \Rightarrow dx = - \sin tdt,}\;\; {\Rightarrow \frac{{dt}}{{dx}} = - \frac{1}{{\sin t}}.} \] Следовательно, \[y' = \frac{{dy}}{{dx}} = \frac{{dy}}{{dt}}\frac{{dt}}{{dx}} = - \frac{1}{{\sin t}}\frac{{dy}}{{dt}},\] \[ {y'' = \frac{{{d^2}y}}{{d{x^2}}} = \frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) } = {\frac{d}{{dt}}\frac{{dt}}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) } = { - \frac{1}{{\sin t}}\frac{d}{{dt}}\left( { - \frac{1}{{\sin t}}\frac{{dy}}{{dt}}} \right) } = {\frac{1}{{\sin t}}\left[ {\frac{d}{{dt}}\left( {\frac{1}{{\sin t}}} \right)\frac{{dy}}{{dt}} + \frac{1}{{\sin t}}\frac{{{d^2}y}}{{d{t^2}}}} \right] } = {\frac{1}{{\sin t}}\left[ {\left( { - \frac{{\cos t}}{{{{\sin }^2}t}}} \right)\frac{{dy}}{{dt}} + \frac{1}{{\sin t}}\frac{{{d^2}y}}{{d{t^2}}}} \right] } = {\frac{1}{{{{\sin }^2}t}}\left[ {\left( { - \frac{{\cos t}}{{\sin t}}} \right)\frac{{dy}}{{dt}} + \frac{{{d^2}y}}{{d{t^2}}}} \right].} \] Подставим выражения для производных в дифференциальное уравнение: \[\require{cancel} {\left( {1 - {{\cos }^2}t} \right)\frac{1}{{{{\sin }^2}t}}\left[ {\left( { - \frac{{\cos t}}{{\sin t}}} \right)\frac{{dy}}{{dt}} + \frac{{{d^2}y}}{{d{t^2}}}} \right] } - {\cos t\left[ { - \frac{1}{{\sin t}}\frac{{dy}}{{dt}}} \right] + {n^2}y = 0,}\;\; {\Rightarrow \frac{\cancel{{{\sin }^2}t}}{\cancel{{{\sin }^2}t}}\left[ { - \frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}} + \frac{{{d^2}y}}{{d{t^2}}}} \right] + \frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}} + {n^2}y = 0,}\;\; {\Rightarrow - \cancel{\frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}}} + \frac{{{d^2}y}}{{d{t^2}}} + \cancel{\frac{{\cos t}}{{\sin t}}\frac{{dy}}{{dt}}} + {n^2}y = 0.} \] В результате дифференциальное уравнение принимает более компактный вид: \[\frac{{{d^2}y}}{{d{t^2}}} + {n^2}y = 0.\] Общее решение последнего уравнения определяется формулой \[y\left( t \right) = {C_1}\cos \left( {nt} \right) + {C_2}\sin\left( {nt} \right),\] которую можно записать также в форме \[y\left( t \right) = C\cos \left( {nt + \alpha } \right).\] Здесь \({C_1},\) \({C_2},\) \(C\) и \(\alpha\) − произвольные действительные числа. Для простоты можно положить \(\alpha = 0.\) Тогда общее решение исходного уравнения Чебышева будет описываться выражением \[y\left( x \right) = C\cos \left( {n\arccos x} \right).\] В этой формуле \(n\) означает любое действительное число. В случае, когда \(n\) − целое число, данная формула описывает полиномы Чебышева первого рода. 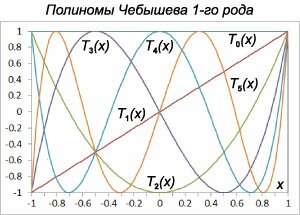Полиномом Чебышева первого рода называется функция \[{T_n}\left( x \right) = \cos \left( {n\arccos x} \right),\] где \(\left| x \right| \le 1\) и \(n = 0,1,2,3, \ldots \) Далее мы покажем, что указанную функцию можно представить в виде алгебраического многочлена. Для \(n = 0\) и \(n = 1\) имеем \[{T_0}\left( x \right) = \cos 0 = 1,\] \[{T_1}\left( x \right) = \cos \left( {\arccos x} \right) = x.\] Полагая \(x = \cos t,\) можно записать: \[{T_1}\left( t \right) = \cos \left( {\arccos \left( {\cos t} \right)} \right) = \cos t,\] \[{T_n}\left( t \right) = \cos \left( {n\arccos \left( {\cos t} \right)} \right) = \cos \left( {nt} \right),\] \[{T_{n - 1}}\left( t \right) = \cos \left( {\left( {n - 1} \right)\arccos \left( {\cos t} \right)} \right) = \cos \left( {\left( {n - 1} \right)t} \right),\] \[{T_{n + 1}}\left( t \right) = \cos \left( {\left( {n + 1} \right)\arccos \left( {\cos t} \right)} \right) = \cos \left( {\left( {n + 1} \right)t} \right).\] Поскольку \[ {\cos \left( {\left( {n - 1} \right)t} \right) + \cos \left( {\left( {n + 1} \right)t} \right) } = {2\cos \frac{{\left( {n - 1} \right)t + \left( {n + 1} \right)t}}{2}\cos \frac{{\left( {n - 1} \right)t - \left( {n + 1} \right)t}}{2} } = {2\cos \frac{{2nt}}{2}\cos \frac{{\left( { - 2t} \right)}}{2} } = {2\cos \left( {nt} \right)\cos t,} \] то мы получаем следующую систему рекуррентных соотношений для полиномов Чебышева первого рода: \[ {{T_{n - 1}} + {T_{n + 1}} = 2{T_n}{T_1},}\;\; {\Rightarrow {T_{n + 1}} = 2{T_n}x - {T_{n - 1}}.} \] Теперь можно легко вычислить полиномы Чебышева более высокого порядка: \[{T_2} = 2{T_1}\left( x \right)x - {T_0} = 2{x^2} - 1,\] \[ {{T_3} = 2{T_2}\left( x \right)x - {T_1} } = {2\left( {2{x^2} - 1} \right)x - x } = {4{x^3} - 3x,} \] \[ {{T_4} = 2{T_3}\left( x \right)x - {T_2} } = {2\left( {4{x^3} - 3x} \right)x - \left( {2{x^2} - 1} \right) } = {8{x^4} - 8{x^2} + 1,} \] \[ {{T_5} = 2{T_4}\left( x \right)x - {T_3} } = {2\left( {8{x^4} - 8{x^2} + 1} \right)x - \left( {4{x^3} - 3x} \right) } = {16{x^5} - 20{x^3} + 5x,} \] и так далее... 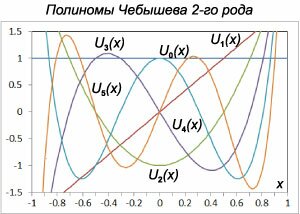Полиномы Чебышева второго рода также можно определить с помощью рекуррентных соотношений: \[ {U_n}\left( x \right) = \begin{cases} 1, & \text{если}\;\;n = 0 \\ 2x, & \text{если}\;\;n = 1 \\ 2x{U_{n - 1}}\left( x \right) - {U_{n - 2}}\left( x \right), & \text{если}\;\;n \le 2 \end{cases}. \] Полиномы Чебышева второго рода являются решениями дифференциального уравнения Чебышева вида \[\left( {1 - {x^2}} \right)y'' - 3xy' + n\left( {n + 2} \right)y = 0.\] Графики полиномов Чебышева первого и второго рода показаны, соответственно, на рисунках \(1\) и \(2.\)

   Пример 1

Найти общее решение уравнения \(\left( {1 - {x^2}} \right)y'' - xy' + 2y = 0\) при \(\left| x \right| < 1.\) Данное уравнение является уравнением Чебышева с дробным параметром \(n = \sqrt 2 .\) Его общее решение можно записать в тригонометрической форме: \[y\left( x \right) = {C_1}\cos \left( {\sqrt 2 \arccos x} \right) + {C_2}\sin\left( {\sqrt 2 \arccos x} \right),\] где \({C_1},\) \({C_2}\) − произвольные постоянные. Заметим, что в данном случае решение не выражается через полиномы Чебышева из-за дробного параметра \(\sqrt 2.\)

   Пример 2

Найти общее решение дифференциального уравнения \(\left( {1 - {x^2}} \right)y'' - xy' + 4y = 0\) при \(\left| x \right| < 1.\) Здесь мы имеем дело с уравнением Чебышева с параметром \(n = 2.\) Поэтому можно прямо записать общее решение в форме: \[y\left( x \right) = {C_1}\cos \left( {2\arccos x} \right) + {C_2}\sin\left( {2\arccos x} \right),\] где \({C_1},\) \({C_2}\) − произвольные постоянные.

Это решение можно выразить через полиномы Чебышева первого рода. Поскольку \[\cos \left( {2\arccos x} \right) = {T_2}\left( x \right) = 2{x^2} - 1,\] то получаем окончательный ответ в следующем виде: \[ {y\left( x \right) = {C_1}\cos \left( {2\arccos x} \right) + {C_2}\sqrt {1 - {\cos^2}\left( {2\arccos x} \right)} } = {{C_1}{T_2}\left( x \right) + {C_2}\sqrt {1 - T_2^2\left( x \right)} } = {{C_1}\left( {2{x^2} - 1} \right) + {C_2}\sqrt {1 - {{\left( {2{x^2} - 1} \right)}^2}} } = {{C_1}\left( {2{x^2} - 1} \right) + {C_2}\sqrt {1 - \left( {4{x^4} - 4{x^2} + 1} \right)} } = {{C_1}\left( {2{x^2} - 1} \right) + 2{C_2}x\sqrt {1 - {x^2}} .} \]