|
Уравнение цепной линии
|
||||||||||||
|
Цепной линией называется плоская кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной в обоих концах и провисающей под действием силы тяжести.
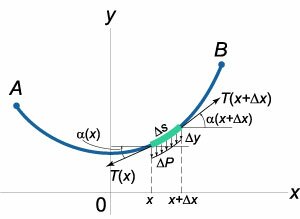
Цепная линия по форме напоминает параболу (рисунок \(1\)). Так считалось долгое время. В начале \(17\) века Галилео Галилей высказал сомнение, что висящая цепь в действительности является параболой. Однако строгое доказательство и точный вывод были получены лишь полвека спустя − после того, как Исаак Ньютон и Готфрид Вильгельм Лейбниц разработали основы математического анализа. Решение задачи о цепной линии было опубликовано в \(1691\) году Христианом Гюйгенсом, Готфридом Вильгельмом Лейбницем и Иоганном Бернулли. Ниже мы рассмотрим вывод уравнения цепной линии и некоторые его вариации. Пусть тяжелая однородная нить подвешена в точках \(А, В,\) которые могут находиться на разной высоте (рисунок \(2\)).
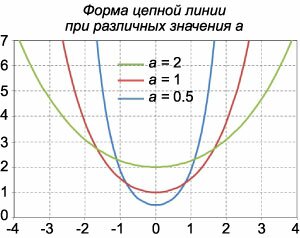
Условия равновесия выделенного элемента длиной \(\Delta s\) в проекциях на оси \(Ox\) и \(Oy\) записываются в виде: \[ - T\left( x \right)\cos \alpha \left( x \right) + T\left( {x + \Delta x} \right)\cos \alpha \left( {x + \Delta x} \right) = 0,\] \[ - T\left( x \right)\sin\alpha \left( x \right) + T\left( {x + \Delta x} \right)\sin\alpha \left( {x + \Delta x} \right) - \Delta P = 0. \] Из первого уравнения видно, что горизонтальная компонента силы натяжения \(T\left( x \right)\) всегда постоянна: \[T\left( x \right)\cos \alpha \left( x \right) = {T_0} = \text{const}.\] Переходя во втором уравнении к дифференциалам, можно записать его в виде \[d\left( {T\left( x \right)\sin\alpha \left( x \right)} \right) = dP\left( x \right).\] Поскольку \(T\left( x \right) = \large\frac{{{T_0}}}{{\cos\alpha \left( x \right)}}\normalsize,\) то получаем \[ {d\left( {{T_0}\tan\alpha \left( x \right)} \right) = dP\left( x \right),}\;\; {\Rightarrow {T_0}d\left( {\tan\alpha \left( x \right)} \right) = dP\left( x \right).} \] Учтем, что \(\tan \alpha \left( x \right) = {\large\frac{{dy}}{{dx}}\normalsize} = y',\) так что уравнение равновесия записывается в дифференциальном виде как \[ {{T_0}d\left( {y'} \right) = dP\left( x \right),}\;\; {\Rightarrow {T_0}d\left( {y'} \right) = \rho gAds.} \] Элемент длины \(\Delta s\) можно выразить по формуле \[ds = \sqrt {1 + {{\left( {y'} \right)}^2}} dx.\] В результате получаем дифференциальное уравнение цепной линии: \[ {{T_0}\frac{{dy'}}{{dx}} = \rho gA\sqrt {1 + {{\left( {y'} \right)}^2}} ,}\;\; {\Rightarrow {T_0}y'' = \rho gA\sqrt {1 + {{\left( {y'} \right)}^2}} .} \] Это уравнение допускает понижение порядка. Обозначив \(y' = z,\) представим его в виде уравнения первого порядка: \[{T_0}z' = \rho gA\sqrt {1 + {z^2}} .\] Последнее уравнение решается методом разделения переменных. \[ {{T_0}dz = \rho gA\sqrt {1 + {z^2}} dx,}\;\; {\Rightarrow \frac{{dz}}{{\sqrt {1 + {z^2}} }} = \frac{{\rho gA}}{{{T_0}}}dx,}\;\; {\Rightarrow \int {\frac{{dz}}{{\sqrt {1 + {z^2}} }}} = \frac{{\rho gA}}{{{T_0}}}\int {dx} ,}\;\; {\Rightarrow \ln \left( {z + \sqrt {1 + {z^2}} } \right) = \frac{x}{a} + {C_1}.} \] Здесь мы обозначили \(\large\frac{{\rho gA}}{{{T_0}}}\normalsize\) через \(\large\frac{1}{a}\normalsize.\) Касательная к цепной линии в нижней точке параллельна оси \(Ox.\) Следовательно, \[z\left( {x = 0} \right) = y'\left( {x = 0} \right) = 0.\] Отсюда определим константу \({C_1}:\) \[\ln 1 = 0 + {C_1},\;\; \Rightarrow {C_1} = 0.\] Итак, мы имеем следующее уравнение: \[z + \sqrt {1 + {z^2}} = {e^{\large\frac{x}{a}\normalsize}}.\] Умножим обе части данного уравнения на сопряженное выражение \(z - \sqrt {1 + {z^2}}. \) Получаем: \[ {\left( {z + \sqrt {1 + {z^2}} } \right)\left( {z - \sqrt {1 + {z^2}} } \right) = \left( {z - \sqrt {1 + {z^2}} } \right){e^{\large\frac{x}{a}\normalsize}},}\;\; {\Rightarrow {z^2} - \left( {1 + {z^2}} \right) = \left( {z - \sqrt {1 + {z^2}} } \right){e^{\large\frac{x}{a}\normalsize}},}\;\; {\Rightarrow - 1 = \left( {z - \sqrt {1 + {z^2}} } \right){e^{\large\frac{x}{a}\normalsize}},}\;\; {\Rightarrow z - \sqrt {1 + {z^2}} = - {e^{ - \large\frac{x}{a}\normalsize}}.} \] Складывая с предыдущим уравнением, находим выражение для \(z = y':\) \[\require{cancel} {z + \cancel{\sqrt {1 + {z^2}}} + z - \cancel{\sqrt {1 + {z^2}}} = {e^{\large\frac{x}{a}\normalsize}} - {e^{ - \large\frac{x}{a}\normalsize}},}\;\; {\Rightarrow z = \frac{{{e^{\large\frac{x}{a}\normalsize}} - {e^{ - \large\frac{x}{a}\normalsize}}}}{2} = \sinh \frac{x}{a},}\;\; {\Rightarrow y' = \sinh \frac{x}{a}.} \] Интегрируем еще раз и получаем окончательное красивое выражение для формы цепной линии: \[y = a\cosh \frac{x}{a}.\] Итак, цепная линия описывается гиперболическим косинусом. Ее форма однозначно определяется параметром \(a = \large\frac{{{T_0}}}{{\rho gA}}\normalsize,\) зависимость от которого показана на рисунке \(3.\)
В архитектуре и строительстве арки в форме перевернутой цепной линии (такие как арка Сааринена в Сент-Луисе, показанная на рисунке \(4\)) обладают высокой устойчивостью благодаря тому, что внутренние силы сжатия идеально скомпенсированы и не вызывают прогиба. Цепная линия обладает еще одним интересным свойством. При вращении цепной линии вокруг оси \(Ox\) образуется поверхность, которая называется катеноидом. Катеноид представляет собой минимальную поверхность, т.е. любой ее участок будет по площади меньше, чем всякая другая поверхность, ограниченная тем же контуром. В частности, мыльная пленка между двумя окружностями, стремясь минимизировать свободную энергию, принимает форму катеноида. |
||||||||||||
|
Пример 1
|
||||||||||||
|
Определить форму каната подвесного моста.
Решение. Тогда условие равновесия дифференциального элемента каната \(ds\) можно записать в виде \[ {{T_0}d\left( {y'} \right) = dP\left( x \right) = \mu dx,}\;\; {\Rightarrow y'' = \frac{\mu }{{{T_0}}}.} \] Дважды интегрируя полученное простейшее дифференциальное уравнение, находим форму каната: \[ {y' = \frac{\mu }{{{T_0}}}x + {C_1},}\;\; {\Rightarrow y = \frac{\mu }{{2{T_0}}}{x^2} + {C_1}x + {C_2},} \] где \({C_1},{C_2}\) − постоянные интегрирования, зависящие от начальных условий. Таким образом, канат подвесного моста принимает форму не цепной линии, а параболы. Так выглядит, например, знаменитый мост "Золотые Ворота" в Сан-Франциско (рисунок \(5\)).
|
||||||||||||
|
Пример 2
|
||||||||||||
|
Определить форму неоднородной цепной линии равного сопротивления.
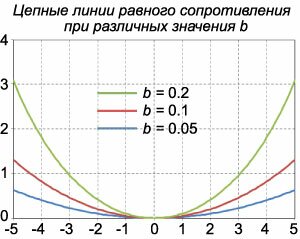
Решение. В этом случае условия равновесия произвольного элемента нити (рисунок \(1\)) записываются в виде \[T\cos \alpha = {T_0},\;\;T\sin \alpha = \int {\rho gA\left( s \right)ds} .\] Здесь \({T_0}\) − горизонтальная составляющая силы натяжения, \(\alpha\) − угол между касательной к цепной линии и осью \(Ox,\) \(\rho\) − объемная плотность материала нити, \(g\) − ускорение свободного падения, \({A\left( s \right)}\) − площадь сечения нити, которая в данной задаче является переменной величиной. Из первого уравнения выразим \(T:\) \[T = \frac{{{T_0}}}{{\cos \alpha }}.\] Подставим во второе уравнение: \[ {\frac{{{T_0}}}{{\cos \alpha }}\sin \alpha = \int {\rho gA\left( s \right)ds} ,}\;\; {\Rightarrow {T_0}\tan\alpha = \rho g\int {A\left( s \right)ds} .} \] Учтем, что \(\tan\alpha = {\large\frac{{dy}}{{dx}}\normalsize} = y'.\) Поэтому можно записать: \[{T_0}y' = \rho g\int {A\left( s \right)ds} .\] Поскольку напряжение \(\sigma\) равно \(\sigma = \large\frac{T}{A}\normalsize,\) то в правую часть уравнения подставим выражение \(A = {\large\frac{T}{\sigma }\normalsize} = {\large\frac{{{T_0}}}{{\sigma \cos \alpha }}\normalsize}.\) Тогда наше уравнение принимает вид: \[ {{T_0}y' = \rho g\int {\frac{{{T_0}}}{{\sigma \cos \alpha }}ds} ,}\;\; {\Rightarrow y' = \rho g\int {\frac{{ds}}{{\sigma \cos \alpha }}} .} \] По условию задачи напряжение \(\sigma\) должно быть одинаковым во всех сечениях. Поэтому вынесем \(\sigma\) из-под знака интеграла. \[y' = \frac{{\rho g}}{\sigma }\int {\frac{{ds}}{{\cos \alpha }}} .\] Продифференцируем обе части по переменной \(s:\) \[ {\frac{d}{{ds}}\left( {y'} \right) = \frac{{\rho g}}{\sigma }\frac{1}{{\cos \alpha }},}\;\; {\Rightarrow \frac{d}{{dx}}\frac{{dx}}{{ds}}\left( {y'} \right) = \frac{{\rho g}}{\sigma }\frac{1}{{\cos \alpha }}.} \] Поскольку \(\cos \alpha = \large\frac{{dx}}{{ds}}\normalsize,\) то имеем следующее дифференциальное уравнение: \[ {\frac{1}{{\frac{{ds}}{{dx}}}}y'' = \frac{{\rho g}}{\sigma }\frac{{ds}}{{dx}},}\;\; {\Rightarrow y'' = \frac{{\rho g}}{\sigma }{\left( {\frac{{ds}}{{dx}}} \right)^2},}\;\; {\Rightarrow y'' = \frac{{\rho g}}{\sigma }\left[ {1 + {{\left( {y'} \right)}^2}} \right].} \] Мы получили дифференциальное уравнение вида \(F\left( {y',y''} \right) = 0,\) описывающее форму нити равного сопротивления. Данное уравнение легко проинтегрировать, разделяя переменные: \[ {\frac{{d\left( {y'} \right)}}{{1 + {{\left( {y'} \right)}^2}}} = \frac{{\rho g}}{\sigma }dx,}\;\; {\Rightarrow \int {\frac{{d\left( {y'} \right)}}{{1 + {{\left( {y'} \right)}^2}}}} = \frac{{\rho g}}{\sigma }\int {dx} ,}\;\; {\Rightarrow \arctan \left( {y'} \right) = \frac{{\rho g}}{\sigma }x + {C_1}.} \] С учетом начального условия \(y'\left( {x = 0} \right) = 0\) находим, что константа \({C_1}\) равна \(0.\) Поэтому \[y' = \tan \left( {\frac{{\rho g}}{\sigma }x} \right).\] Интегрируем еще раз: \[ {y = \int {\tan \left( {\frac{{\rho g}}{\sigma }x} \right)dx} } = { - \frac{\sigma }{{\rho g}}\ln \cos \left( {\frac{{\rho g}}{\sigma }x} \right) + {C_2}.} \] Константу \({C_2}\) можно положить равной \(0\) при соответствующем выборе системы координат. Итак, форма цепной линии равного сопротивления определяется функцией \[y = - \frac{1}{b}\ln \cos \left( {bx} \right),\] где \(b\) обозначает \(\large\frac{{\rho g}}{\sigma }\normalsize.\) График этой функции при различных значениях \(b\) представлен на рисунке \(6.\) |
||||||||||||