Уравнение Ван-дер-Ваальса

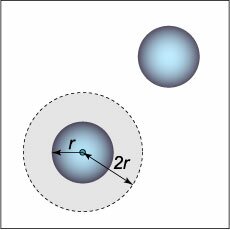
Состояние определенной массы любого вещества можно описать с помощью трех параметров: давления \(p\), объема \(V\) и температуры \(T\). Эти параметры связаны между собой. Их взаимосвязь описывается уравнением состояния, которое в общем случае имеет вид: \[F\left( {p,V,T} \right) = 0.\] Конкретный вид уравнения зависит от свойств вещества. Например, разреженный газ при достаточно высокой температуре хорошо описывается моделью идеального газа. Уравнением состояния для него является известное уравнение Клапейрона (\(1799-1864\)), предложенное в \(1834\) году: \[pV = \frac{m}{M}RT.\] Здесь \(m\) − масса газа, \(M\) − молярная масса (т.е. масса одного моля данного газа), \(R\) − универсальная газовая постоянная. Для одного моля газа это уравнение принимает следующий вид: \[pV = RT.\] Проведенные позднее эксперименты выявили отклонение в поведении реальных газов от законов идеального газа. Эти результаты были обобщены голландским физиком Яном Дидериком Ван-дер-Ваальсом (\(1837-1923\)), который в \(1873\) году предложил более точное уравнение состояния реального газа. Оно называется уравнением Ван-дер-Ваальса и в расчете на один моль записывается в виде \[\left( {p + \frac{a}{{{V^2}}}} \right)\left( {V - b} \right) = RT.\] Данное уравнение учитывает силы притяжения и отталкивания, действующие между молекулами. Силы притяжения учитываются благодаря пристеночному эффекту. Действительно, для частиц, находящихся во внутренней области, силы притяжения со стороны других молекул в среднем скомпенсированы. Однако для частиц вблизи стенок сосуда возникает нескомпенсированная сила притяжения \(f,\) направленная внутрь сосуда. Эта сила, с одной стороны, пропорциональна концентрации частиц \(n\) в сосуде, а с другой стороны − пропорциональна концентрации частиц в пристеночном слое. В результате получаем: \[f \sim {n^2} \sim \frac{1}{{{V^2}}},\] где \(n\) − концентрация молекул в сосуде, \(V\) − объем \(1\) моля газа.

Рассмотренный эффект притяжения молекул пристеночного слоя приводит к уменьшению давления на стенки сосуда. При формальном переходе от уравнения Клапейрона к уравнению Ван-дер-Ваальса это соответствует замене \[p \to p + \frac{a}{{{V^2}}},\] где \(a\) − коэффициент, зависящий от конкретного газа и размеров сосуда.

Силы отталкивания между молекулами в модели Ван-дер-Ваальса учитываются очень просто: предполагается, что молекулы имеют форму шара радиуса \(r\) и не могут приблизиться друг к другу на расстояние между центрами, меньшее чем \(2r.\) Можно считать, что вокруг одной из двух молекул существует "запрещенный" (исключенный) объем (рисунок \(1\)), равный \[\frac{4}{3}\pi {\left( {2r} \right)^3} = 8 \cdot \frac{4}{3}\pi {r^3}.\] Следовательно, в расчете на одну молекулу исключенный объем равен \[{b_0} = 4 \cdot \frac{4}{3}\pi {r^3} = 4{V_0},\] где \({V_0}\) − объем одной молекулы.

В результате , если в уравнении Клапейрона объем пространства, доступного для движения молекул, был равен \(V,\) то теперь он становится равным \[V - {N_A}{b_0} = V - b,\] где \({N_A}\) − число Авогадро (равное числу молекул в одном моле газа), \(b\) − исключенный объем, обусловленный отталкиванием молекул. 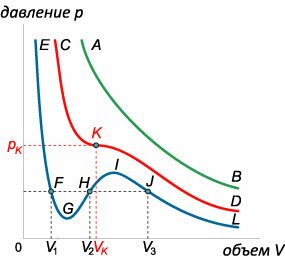Предполагая, что силы притяжения и отталкивания молекул действуют совместно и заменяя \(p\) и \(V\) новыми выражениями, получаем из уравнения Клапейрона уравнение Ван-дер-Ваальса: \[\left( {p + \frac{a}{{{V^2}}}} \right)\left( {V - b} \right) = RT.\] При фиксированной температуре уравнение Ван-дер-Ваальса описывает зависимость \(p\left( V \right).\) На плоскости \(pV\) такая зависимость изображается в виде семейства изотерм, каждая из которых соответствует определенной температуре. Для исследования характера этой зависимости преобразуем уравнение Ван-дер-Ваальса к следующему виду: \[ {\left. {\left( {p + \frac{a}{{{V^2}}}} \right)\left( {V - b} \right) = RT\;} \right| \cdot {V^2},}\;\; {\Rightarrow \left( {p{V^2} + a} \right)\left( {V - b} \right) = RT{V^2},}\;\; {\Rightarrow p{V^3} + aV - pb{V^2} - ab - RT{V^2} = 0,}\;\; {\Rightarrow \left. {p{V^3} - \left( {pb + RT} \right){V^2} + aV - ab = 0\;} \right|:p,}\;\; {\Rightarrow {V^3} - \left( {b + \frac{{RT}}{p}} \right){V^2} + \frac{a}{p}V - \frac{{ab}}{p} = 0.} \] При фиксированном значении \(p\) полученное уравнение является уравнением третьей степени по переменной \(V\). Известно, что кубическое уравнение может иметь \(1\) или \(3\) действительных корня. Первый случай встречается при высоких температурах \(T\) (зеленая изотерма \(AB\) на рисунке \(3\)). При понижении температуры на изотерме появляется волнообразный участок. В этом случае существует три корня (синяя изотерма \(EFGHIJL\)). Переход между двумя типами изотерм происходит при определенной температуре \({T_K},\) которая называется критической температурой. В критической точке газ характеризуется критическими параметрами \({T_K}\), \({p_K}\) и \({V_K},\) которые определяются лишь свойствами газа. С алгебраической точки зрения изотерма в критической точке имеет три действительных корня, которые равны между собой. Это обстоятельство позволяет легко вычислить значения \({T_K}\), \({p_K}\) и \({V_K}.\) Действительно, в этом случае уравнение состояния газа \[{V^3} - \left( {b + \frac{{RT}}{p}} \right){V^2} + \frac{a}{p}V - \frac{{ab}}{p} = 0\] должно записываться как \[{\left( {V - {V_K}} \right)^3} = 0.\] Раскрывая куб разности и приравнивая коэффициенты при соответствующих степенях \(V,\) находим выражения для критических параметров: \[ {{\left( {V - {V_K}} \right)^3} = 0,}\;\; {\Rightarrow {V^3} - 3{V^2}{V_K} + 3V{V_K} - V_K^3 = 0.} \] Учтем, что в критической точке \(p = {p_K}\), \(T = {T_K}.\) Следовательно, получаем: \[ {\left\{ \begin{array}{l} - \left( {b + \frac{{RT}}{p}} \right) = - 3{V_K}\\ \frac{a}{{{p_K}}} = 3V_K^2\\ - \frac{{ab}}{{{p_K}}} = - V_K^3 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} b + \frac{{RT}}{p} = 3{V_K}\\ \frac{a}{{{p_K}}} = 3V_K^2\\ \frac{{ab}}{{{p_K}}} = V_K^3 \end{array} \right..} \] Разделим третье уравнение на второе: \[\require{cancel} {\frac{{\cancel{a}b \cdot \cancel{p_K}}}{{\cancel{p_K} \cdot \cancel{a}}} = \frac{{V_K^{\cancel{3}}}}{{3\cancel{V_K^2}}},}\;\; {\Rightarrow {V_K} = 3b.} \] Из второго уравнения определяем \({p_K}:\) \[ {{p_K} = \frac{a}{{3V_K^2}} } = {\frac{a}{{3 \cdot {{\left( {3b} \right)}^2}}} } = {\frac{a}{{27{b^2}}}.} \] Наконец, из первого уравнения находим критическую температуру \({T_K}:\) \[ {{T_K} = \frac{{\left( {3{V_K} - b} \right){p_K}}}{R} } = {\frac{{\left( {3 \cdot 3b - b} \right) \cdot \frac{a}{{27{b^2}}}}}{R} } = {\frac{{8a}}{{27bR}}.} \] Итак, критические параметры газа в модели Ван-дер-Ваальса зависят лишь от величин \(a, b\) и определяются формулами \[ {{V_K} = 3b,}\;\;\; {{p_K} = \frac{a}{{27{b^2}}},}\;\;\; {{T_K} = \frac{{8a}}{{27bR}}.} \] Заметим, что мы нашли критические величины без использования производной. Можно показать, что в критической точке с параметрами \({V_K}\), \({p_K}\), \({T_K}\) первая и вторая производная функции \(p\left( V \right)\) равны нулю (смотрите Пример \(1\)). Используя критические параметры \({V_K}\), \({p_K}\) и \({T_K}\) можно перейти к безразмерным переменным: \[ {\varphi = \frac{V}{{{V_K}}},}\;\;\; {\pi = \frac{p}{{{p_K}}},}\;\;\; {\tau = \frac{T}{{{T_K}}}} \] и переписать уравнение Ван-дер-Ваальса в приведенной форме: \[ {V = \varphi {V_K},\;p = \pi {p_K},\;T = \tau {T_K},}\;\; {\Rightarrow \left( {\pi {p_K} + \frac{a}{{{{\left( {\varphi {V_K}} \right)}^2}}}} \right)\left( {\varphi {V_K} - b} \right) = R\tau {T_K},}\;\; {\Rightarrow \left( {\frac{{\pi a}}{{27{b^2}}} + \frac{a}{{{{\left( {3b} \right)}^2}{\varphi ^2}}}} \right)\left( {3b\varphi - b} \right) = R\tau \cdot \frac{{8a}}{{27bR}},}\;\; {\Rightarrow \left( {\pi + \frac{3}{{{\varphi ^2}}}} \right)\left( {3\varphi - 1} \right) = 8\tau .} \] Данное уравнение является более универсальным, чем исходное уравнение Ван-дер-Ваальса. Изотермы для различных веществ, построенные в соответствии с приведенным уравнением, будут совпадать при одинаковых значениях \(\tau.\) Состояния разных тел, которые описываются одинаковыми приведенными параметрами \(\pi,\) \(\varphi,\) \(\tau,\) называются соответственными состояниями. Если два каких-либо тела или вещества обладают любыми двумя одинаковыми приведенными параметрами, то они имеют и третью одинаковую величину. Это универсальное свойство называется законом соответственных состояний.

Рассмотрим еще один интересный инвариант. Поскольку в модели Ван-дер-Ваальса критические величины \({V_K}\), \({p_K}\), \({T_K}\) выражаются лишь через два параметра \(a\) и \(b,\) мы можем составить комбинацию этих величин, не зависящую от \(a\) и \(b.\) Можно записать следующее соотношение: \[ {\frac{{{p_K}{V_K}}}{{{T_K}}} } = {\frac{{3b \cdot \frac{a}{{27{b^2}}}}}{{\frac{{8a}}{{27bR}}}} } = {\frac{{3\cancel{a}\cancel{b} \cdot \cancel{27}\cancel{b}R}}{{\cancel{27}\cancel{b^2} \cdot 8\cancel{a}}} } = {\frac{{3R}}{8}}\;\;\; {\text{или}\;\;\;\frac{{{p_K}{V_K}}}{{{T_K}R}} } = {\frac{3}{8} = 0,375.} \] Это отношение называется критическим коэффициентом и не зависит ни от каких величин, характеризующих то или иное вещество, т.е. является инвариантной величиной. Рассмотрим снова уравнение Ван-дер-Ваальса при температурах не выше критической: \(T < {T_K}.\) В этом случае изотермы имеют волнообразный характер. Участок такой изотермы между минимумом и максимумом характеризуется положительной производной \(\large\frac{{dp}}{{dV}}\normalsize > 0,\) что соответствует нестабильному состоянию вещества. При малой флуктуации объема \(dV > 0\) давление газа будет также возрастать (так как \(dp > 0\)), что приведет к взрывному расширению газа. При отрицательной флуктуации \(dV < 0,\) наоборот, будет происходить быстрый коллапс вещества.

На самом деле в этой области на \(pV\)-диаграмме происходит фазовый переход "газ-жидкость", сопровождающийся значительным изменением объема \(V\) при постоянном давлении \(p\) и постоянной температуре \(T.\) Такой переход на \(pV\)-диаграмме изображается прямолинейным горизонтальным участком (отрезок \(FJ\) на рисунке \(4\)). В сосуде при этом возникает двухфазное состояние газ + жидкость. При перемещении фазовой точки влево вдоль отрезка \(JF\) объем газа уменьшается, а объем жидкости, соответственно, возрастает.

Расположение горизонтального участка \(FJ\) определяется из термодинамических соображений − на основании т.н. правила Максвелла, согласно которому площади криволинейных фигур \(FGH\) и \(HIJ\) должны быть равными (смотрите выше рисунок \(4\)).

Множество начальных и конечных точек горизонтальных участков при разных температурах \(T\) (где \(T \le {T_K}\)) образует кривую, которая называется бинодалью. Кривая, проходящая через точки минимума и точки максимума всех изотерм при \(T \le {T_K},\) называется спинодалью.

Нестабильные состояния (для которых \(\large\frac{{dp}}{{dV}}\normalsize > 0\)) находятся внутри области, ограниченной спинодалью. Область диаграммы между спинодалью и бинодалью в принципе удовлетворяет критерию устойчивости \(\large\frac{{dp}}{{dV}}\normalsize < 0.\) Поэтому состояния вещества, которые реализуются в этой области, называются метастабильными состояниями. В левой половине указанной области образуется перегретая жидкость, а в правой половине − переохлажденный пар.

Удивительно, что такая простая модель реального газа, в которой лишь грубо учитываются межмолекулярные силы, способна отражать реальный набор различных состояний газа и жидкости. Кроме регулярного газа и жидкости, фазового перехода "газ-жидкость" и рассмотренных метастабильных состояний, модель Ван-дер-Ваальса фиксирует также такое экзотическое явление, как растянутая жидкость (участок \(MNS\) на рисунке \(4\)). Это состояние жидкости является неустойчивым.

В приведенных ниже задачах мы акцентируем внимание на исследовании уравнения Ван-дер-Ваальса с помощью производной.

   Пример 1

Показать, что в критической точке первая и вторая производные от давления по объему при постоянной температуре равны нулю. Уравнение изотермы в модели Ван-дер-Ваальса записывается в виде \[p\left( V \right) = \frac{{RT}}{{V - b}} - \frac{a}{{{V^2}}}.\] Запишем выражения для первой и второй производной, считая температуру \(T\) постоянной: \[ {{\left( {\frac{{\partial p}}{{\partial V}}} \right)_T} } = {p'\left( V \right) } = {{\left( {\frac{{RT}}{{V - b}} - \frac{a}{{{V^2}}}} \right)^\prime } } = { - \frac{{RT}}{{{{\left( {V - b} \right)}^2}}} + \frac{{2a}}{{{V^3}}};} \] \[ {{\left( {\frac{{{\partial ^2}p}}{{\partial {V^2}}}} \right)_T} } = {p''\left( V \right) } = {{\left( { - \frac{{RT}}{{{{\left( {V - b} \right)}^2}}} + \frac{{2a}}{{{V^3}}}} \right)^\prime } } = {\frac{{2RT}}{{{{\left( {V - b} \right)}^3}}} - \frac{{6a}}{{{V^4}}}.} \] Найдем значения \(V\) и \(T,\) при которых обе производные равны нулю: \[ {\left\{ \begin{array}{l} p'\left( V \right) = 0\\ p''\left( V \right) = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} - \frac{{RT}}{{{{\left( {V - b} \right)}^2}}} + \frac{{2a}}{{{V^3}}} = 0\\ \frac{{2RT}}{{{{\left( {V - b} \right)}^3}}} - \frac{{6a}}{{{V^4}}} = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} \frac{{RT}}{{{{\left( {V - b} \right)}^2}}} = \frac{{2a}}{{{V^3}}}\\ \frac{{2RT}}{{{{\left( {V - b} \right)}^3}}} = \frac{{6a}}{{{V^4}}} \end{array} \right..} \] Разделим второе уравнение на первое: \[ {\frac{{2RT}}{{{{\left( {V - b} \right)}^3}}}:\frac{{RT}}{{{{\left( {V - b} \right)}^2}}} = \frac{{6a}}{{{V^4}}}:\frac{{2a}}{{{V^3}}},}\;\; {\Rightarrow \frac{{2\cancel{RT} \cdot \cancel{{\left( {V - b} \right)}^2}}}{{{{\left( {V - b} \right)}^{\cancel{3}}} \cdot \cancel{RT}}} = \frac{{6\cancel{a} \cdot \cancel{V^3}}}{{{V^{\cancel{4}}} \cdot 2\cancel{a}}},}\;\; {\Rightarrow \frac{2}{{V - b}} = \frac{3}{V},}\;\; {\Rightarrow 2V = 3\left( {V - b} \right),}\;\; {\Rightarrow 2V = 3V - 3b,}\;\; {\Rightarrow V = 3b.} \] Из первого уравнения находим \(T:\) \[ {\frac{{RT}}{{{{\left( {V - b} \right)}^2}}} = \frac{{2a}}{{{V^3}}},}\;\; {\Rightarrow T = \frac{{2a{{\left( {V - b} \right)}^2}}}{{R{V^3}}} } = {\frac{{2a{{\left( {3b - b} \right)}^2}}}{{R{{\left( {3b} \right)}^3}}} } = {\frac{{2a \cdot 4{b^2}}}{{R \cdot 27{b^3}}} = \frac{{8a}}{{27bR}}.} \] Наконец, вычислим \(p\) из исходного уравнения Ван-дер-Ваальса: \[ {p = \frac{{RT}}{{V - b}} - \frac{a}{{{V^2}}} } = {\frac{{R \cdot \frac{{8a}}{{27bR}}}}{{3b - b}} - \frac{a}{{{{\left( {3b} \right)}^2}}} } = {\frac{{4a}}{{27{b^2}}} - \frac{2}{{9{b^2}}} } = {\frac{a}{{27{b^2}}}.} \] Как видно, полученные значения полностью совпадают с критическими значениями \({V_K}\), \({p_K}\) и \({T_K},\) полученными выше.

Чтобы исследовать характер критической точки более детально, вычислим в ней третью производную: \[ {{\left( {\frac{{{\partial ^3}p}}{{\partial {V^3}}}} \right)_T} } = {p'''\left( V \right) } = {{\left( {\frac{{2RT}}{{{{\left( {V - b} \right)}^3}}} - \frac{{6a}}{{{V^4}}}} \right)^\prime } } = { - \frac{{6RT}}{{{{\left( {V - b} \right)}^4}}} + \frac{{24a}}{{{V^5}}};} \] \[ {\Rightarrow {\left( {\frac{{{\partial ^3}p}}{{\partial {V^3}}}} \right)_{T = {T_K}}} } = {p'''{\left( V \right)_{T = {T_K}}} } = { - \frac{{6R \cdot \frac{{8a}}{{27bR}}}}{{{{\left( {3b - b} \right)}^4}}} + \frac{{24a}}{{{{\left( {3b} \right)}^5}}} } = { - \frac{{3a}}{{27{b^5}}} + \frac{{8a}}{{81{b^5}}} } = {\frac{{ - 9a + 8a}}{{81{b^5}}} } = { - \frac{a}{{81{b^5}}} < 0.} \] Таким образом, в критической точке третья производная от давления по объему при постоянной температуре отрицательна. Следовательно, критическая точка является точкой перегиба функции \(p\left( V \right),\) но в этой точке, согласно третьему достаточному признаку, никакого экстремума не существует.

   Пример 2

Исследовать зависимость \(pV\) от \(V\) для реальных газов. Для идеальных газов произведение давления и объема при изотермическом процессе остается постоянным: \[pV = RT = \text{const}.\] (Уравнение записано для \(1\) моля газа.)

Для реальных газов ситуация может быть совершенно другой. Запишем уравнение ван-дер-Ваальса в виде \[p = \frac{{RT}}{{V - b}} - \frac{a}{{{V^2}}}.\] Следовательно, \[pV = \frac{{RTV}}{{V - b}} - \frac{a}{V}.\] Исследуем произведение \(pV\) на экстремум. Производная от \(pV\) по переменной \(V\) равна: \[ {{\left( {pV} \right)^\prime } } = {{\left( {\frac{{RTV}}{{V - b}} - \frac{a}{V}} \right)^\prime } } = {RT \cdot \frac{{1 \cdot \left( {V - b} \right) - V \cdot 1}}{{{{\left( {V - b} \right)}^2}}} + \frac{a}{{{V^2}}} } = { - \frac{{bRT}}{{{{\left( {V - b} \right)}^2}}} + \frac{a}{{{V^2}}}.} \] Приравнивая производную нулю, найдем критические точки: \[ {{\left( {pV} \right)^\prime } = 0,}\;\; {\Rightarrow - \frac{{bRT}}{{{{\left( {V - b} \right)}^2}}} + \frac{a}{{{V^2}}} = 0,}\;\; {\Rightarrow \frac{{ - bRT{V^2} + a{{\left( {V - b} \right)}^2}}}{{{V^2}{{\left( {V - b} \right)}^2}}} = 0,}\;\; {\Rightarrow - bRT{V^2} + a{\left( {V - b} \right)^2} = 0,}\;\; {\Rightarrow - bRT{V^2} + a\left( {{V^2} - 2bV + {b^2}} \right) = 0,}\;\; {\Rightarrow - bRT{V^2} + a{V^2} - 2abV + a{b^2} = 0,}\;\; {\Rightarrow \left( {a - bRT} \right){V^2} - 2abV + a{b^2} = 0.} \] Получено квадратное уравнение. Его дискриминант равен: \[ {D = 4{a^2}{b^2} - 4a{b^2}\left( {a - bRT} \right) } = {\cancel{4{a^2}{b^2}} - \cancel{4{a^2}{b^2}} + 4a{b^3}RT } = {4a{b^3}RT > 0.} \] Видно, что дискриминант всегда положителен, т.е. квадратное уравнение имеет два действительных корня. Они выражаются следующей формулой: \[ {{V_{1,2}} = \frac{{2ab \pm \sqrt {4a{b^3}RT} }}{{2\left( {a - bRT} \right)}} } = {\frac{{ab \pm ab\sqrt {\frac{b}{a}RT} }}{{a\left( {1 - \frac{b}{a}RT} \right)}} } = {\frac{{b\left( {1 \pm \sqrt {\frac{b}{a}RT} } \right)}}{{1 - \frac{b}{a}RT}}.} \] Первый корень \({V_1}\) со знаком минус в числителе не имеет физического смысла, поскольку \({V_1} < b.\) Поэтому произведение \(pV\) имеет экстремум в точке \[ {{V_2} = {V_{\min}} = \frac{{b\left( {1 + \sqrt {\frac{b}{a}RT} } \right)}}{{1 - \frac{b}{a}RT}} } = {\frac{{b\left( {1 + \sqrt {\frac{b}{a}RT} } \right)}}{{1 - {{\left( {\sqrt {\frac{b}{a}RT} } \right)}^2}}} } = {\frac{{b\cancel{\left( {1 + \sqrt {\frac{b}{a}RT} } \right)}}}{{\left( {1 - \sqrt {\frac{b}{a}RT} } \right)\cancel{\left( {1 + \sqrt {\frac{b}{a}RT} } \right)}}} } = {\frac{b}{{1 - \sqrt {\frac{b}{a}RT} }}.} \] При условии \(1 - \large\frac{b}{a}\normalsize RT > 0\) парабола, соответствующая числителю производной, будет направлена ветвями верх. Поэтому производная при переходе через правый корень \({V_2}\) меняет знак с минуса на плюс. Это означает, что точка \({V_2}\) является минимумом функции \(pV:\) \({V_2} = {V_{\min}}.\)

Таким образом, при сжатии разреженного газа Ван-дер-Ваальса при постоянной температуре произведение \(pV\) сначала уменьшается, достигая минимального значения \({\left( {pV} \right)_{\min }},\) а затем начинает возрастать. Первая стадия объясняется доминированием сил притяжения между молекулами, а вторая стадия связана с усилением вклада отталкивающих сил.

Минимальное значение \({\left( {pV} \right)_{\min }}\) выражается следующим соотношением: \[ {{\left( {pV} \right)_{\min }} } = {\frac{{RT{V_{\min }}}}{{{V_{\min }} - b}} - \frac{a}{{{V_{\min }}}} } = {\frac{{RT \cdot \frac{b}{{1 - \sqrt {\frac{b}{a}RT} }}}}{{\frac{b}{{1 - \sqrt {\frac{b}{a}RT} }} - b}} - \frac{a}{{\frac{b}{{1 - \sqrt {\frac{b}{a}RT} }}}} } = {\frac{{\frac{{bRT}}{\cancel{1 - \sqrt {\frac{b}{a}RT} }}}}{{\frac{{b - b\left( {1 - \sqrt {\frac{b}{a}RT} } \right)}}{\cancel{1 - \sqrt {\frac{b}{a}RT} }}}} - \frac{{a\left( {1 - \sqrt {\frac{b}{a}RT} } \right)}}{b} } = {\frac{{bRT}}{{b\left( {\cancel{1} - \cancel{1} + \sqrt {\frac{b}{a}RT} } \right)}} - \frac{a}{b} + \frac{a}{b}\sqrt {\frac{b}{a}RT} } = {\sqrt {\frac{a}{b}RT} - \frac{a}{b} + \sqrt {\frac{a}{b}RT} } = {2\sqrt {\frac{a}{b}RT} - \frac{a}{b}.} \] Заметим, что значение \({V_{\min}}\) увеличивается с возрастанием температуры и становится равным бесконечности когда температура равна \[T = {T_B} = \frac{a}{{2R}}.\] Эта переходная точка \({T_B}\) называется температурой Бойля. Ниже этой температуры произведение \(pV\) имеет минимум при изотермическом сжатии. А при температуре выше, чем \({T_B},\) произведение \(pV\) в процессе сжатия будет увеличиваться монотонно.

Некоторые газы имеют достаточно низкие значения температуры Бойля. Например, для гелия \(He\) она составляет \({T_B} = 22,6\;\text{K},\) Для неона \(Ne\) она равна \({T_B} = 122,1\;\text{K}.\) Следовательно, при комнатных температурах такие газы демонстрируют монотонную зависимость \(pV\) от \(V.\)