|
Дифференциальное уравнение Бесселя
|
||||||
|
Линейное обыкновенное дифференциальное уравнение второго порядка вида \[{x^2}y'' + xy' = \left( {{x^2} - {v^2}} \right)y = 0\] называется уравнением Бесселя. Число \(v\) называется порядком уравнения Бесселя.
Данное дифференциальное уравнение было названо в честь немецкого математика и астронома Фридриха Вильгельма Бесселя, который подробно исследовал его и показал (в \(1824\) году), что решения уравнения выражаются через специальный класс функций, получивших название цилиндрических функций или функций Бесселя. Конкретное представление общего решения зависит от числа \(v.\) Далее мы отдельно рассмотрим два случая:
Случай 1. Порядок \(v\) является нецелым числом
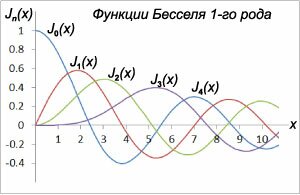
Полагая, что число \(v\) является нецелым и положительным, общее решение уравнения Бесселя можно записать в виде \[y\left( x \right) = {C_1}{J_v}\left( x \right) + {C_2}{J_{ - v}}\left( x \right),\] где \({C_1},\) \({C_2}\) − произвольные постоянные, а \({J_v}\left( x \right),\) \({J_{ - v}}\left( x \right)\) − функции Бесселя первого рода.Функцию Бесселя первого рода можно представить в виде ряда, члены которого выражаются через так называемую гамма-функцию: \[{J_v}\left( x \right) = \sum\limits_{p = 0}^\infty {\frac{{{{\left( { - 1} \right)}^p}}}{{\Gamma \left( {p + 1} \right)\Gamma \left( {p + v + 1} \right)}}{{\left( {\frac{x}{2}} \right)}^{2p + v}}} .\] Гамма-функция является расширением факториальной функции с множества целых на множество действительных чисел. В частности, она обладает следующими свойствами: \[ {\Gamma \left( {p + 1} \right) = p!,}\;\; {\Gamma \left( {p + v + 1} \right) = \left( {v + 1} \right)\left( {v + 2} \right) \cdots \left( {v + p} \right)\Gamma \left( {v + 1} \right).} \] Аналогичным образом записываются функции Бесселя первого рода отрицательного порядка (с индексом \(-v\)). Здесь мы предполагаем, что \(v > 0.\) \[{J_{ - v}}\left( x \right) = \sum\limits_{p = 0}^\infty {\frac{{{{\left( { - 1} \right)}^p}}}{{\Gamma \left( {p + 1} \right)\Gamma \left( {p - v + 1} \right)}}{{\left( {\frac{x}{2}} \right)}^{2p - v}}} .\] Функции Бесселя вычисляются в большинстве математических пакетов. Для примера вид функций Бесселя первого рода порядка от \(v = 0\) до \(v = 4\) показан на рисунке \(1.\) Эти функции можно вычислить также и в MS Excel.
Случай 2. Порядок \(v\) является целым
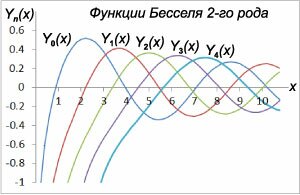
Если порядок \(v\) дифференциального уравнения Бесселя является целым, то функции Бесселя первого рода \({J_v}\left( x \right)\) и \({J_{ - v}}\left( x \right)\) становятся зависимыми друг от друга. В этом случае общее решение уравнения будет описываться другой формулой: \[y\left( x \right) = {C_1}{J_v}\left( x \right) + {C_2}{Y_v}\left( x \right),\] где \({Y_v}\left( x \right)\) − функция Бесселя второго рода. Иногда это семейство функций называют также функциями Неймана или функциями Вебера.Функцию Бесселя второго рода \({Y_v}\left( x \right)\) можно выразить через функции Бесселя первого рода \({J_v}\left( x \right)\) и \({J_{ - v}}\left( x \right):\) \[{Y_v}\left( x \right) = \frac{{{J_v}\left( x \right)\cos \pi v - {J_{ - v}}\left( x \right)}}{{\sin \pi v}}.\] Графики функций \({Y_v}\left( x \right)\) для нескольких первых порядков \(v\) представлены выше на рисунке \(2.\) Примечание: В действительности общее решение дифференциального уравнения Бесселя можно выразить через функции Бесселя первого и второго рода также и для случая нецелого порядка \(v.\)
Некоторые дифференциальные уравнения, приводимые к уравнению Бесселя
1. Еще одним хорошо известным уравнением данного класса является модифицированное уравнение Бесселя, которое получается из регулярного уравнения Бесселя заменой \(x\) на \(-ix.\) Это уравнение имеет вид: \[{x^2}y'' + xy' - \left( {{x^2} + {v^2}} \right)y = 0.\] Решение данного уравнения выражается через так называемые модифицированые функции Бесселя первого и второго рода: \[ {y\left( x \right) = {C_1}{J_v}\left( { - ix} \right) + {C_2}{Y_v}\left( { - ix} \right) } = {{C_1}{I_v}\left( x \right) + {C_2}{K_v}\left( x \right),} \] где \({I_v}\left( x \right)\) и \({K_v}\left( x \right)\) обозначают модифицированные функции Бесселя, соответственно, первого и второго рода.2. Дифференциальное уравнение Эйри, известное в астрономии и физике, записывается в виде: \[y'' - xy = 0\] Его также можно свести к уравнению Бесселя. Решение уравнения Эйри выражается через функции Бесселя дробного порядка \( \pm \large\frac{1}{3}\normalsize:\) \[ {y\left( x \right) } = {{C_1}\sqrt x {J_{\large\frac{1}{3}\normalsize}}\left( {\frac{2}{3}i{x^{\large\frac{3}{2}\normalsize}}} \right) + {C_2}\sqrt x {J_{ - \large\frac{1}{3}\normalsize}}\left( {\frac{2}{3}i{x^{\large\frac{3}{2}\normalsize}}} \right).} \] 3. Дифференциальное уравнение вида \[{x^2}y'' + xy' + \left( {{a^2}{x^2} - {v^2}} \right)y = 0\] отличается от уравнения Бесселя лишь множителем \({a^2}\) перед \({x^2}\) и имеет общее решение в следующем виде: \[y\left( x \right) = {C_1}{J_v}\left( {ax} \right) + {C_2}{Y_v}\left( {ax} \right).\] 4. Похожее дифференциальное уравнение \[{x^2}y'' + axy' + \left( {{x^2} - {v^2}} \right)y = 0\] также сводится к уравнению Бесселя \[{x^2}z'' + xz' + \left( {{x^2} - {n^2}} \right)z = 0\] с помощью подстановки \[y\left( x \right) = {x^{\large\frac{{1 - a}}{2}\normalsize}}z\left( x \right).\] Здесь параметр \({n^2}\) обозначает \[{n^2} = {v^2} + \frac{1}{4}{\left( {a - 1} \right)^2}.\] В результате, общее решение данного дифференциального уравнения определяется формулой \[y\left( x \right) = {x^{\large\frac{{1 - a}}{2}\normalsize}}\left[ {{C_1}{J_n}\left( x \right) + {C_2}{Y_n}\left( x \right)} \right].\] Специальные функции Бесселя широко используются в решении задач математической физики, например, при исследовании
|
||||||
|
Пример 1
|
||||||
|
Решить дифференциальное уравнение \({x^2}y'' + xy' + \left( {3{x^2} - 2} \right)y = 0.\)
Решение. |
||||||
|
Пример 2
|
||||||
|
Решить уравнение \({x^2}y'' + xy' - \left( {4{x^2} + \large\frac{1}{2}\normalsize} \right)y = 0.\)
Решение. |
||||||
|
Пример 3
|
||||||
|
Найти общее решение дифференциального уравнения \({x^2}y'' + 2xy' + \left( {{x^2} - 1} \right)y = 0.\)
Решение. |
||||||