Тройные интегралы в цилиндрических координатах

В цилиндрических координатах положение точки \(M\left( {x,y,z} \right)\) в пространстве \(Oxyz\) определяется тремя числами − \(\rho, \varphi, z,\) где \(\rho\) − длина радиуса-вектора проекции точки \(M\) на плоскость \(Oxy,\) \(\varphi\) − угол, образованный этим радиусом-вектором с осью \(Ox\) (рисунок \(1\)), \(z\) − проекция на ось \(Oz\) (ее значение одинаково в декартовых и цилиндрических координатах). Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями \[ {x = \rho \cos \varphi ,}\;\; {y = \rho \sin \varphi ,}\;\; {z = z.} \] Здесь предполагается, что \[ {\rho \ge 0,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {- \infty < z < \infty .} \] Якобиан перехода от декартовых координат к цилиндрическим равен \[ {I\left( {\rho ,\varphi ,z} \right) } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \rho }}}&{\frac{{\partial x}}{{\partial \varphi }}}&{\frac{{\partial x}}{{\partial z}}}\\ {\frac{{\partial y}}{{\partial \rho }}}&{\frac{{\partial y}}{{\partial \varphi }}}&{\frac{{\partial y}}{{\partial z}}}\\ {\frac{{\partial z}}{{\partial \rho }}}&{\frac{{\partial z}}{{\partial \varphi }}}&{\frac{{\partial z}}{{\partial z}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \rho \sin \varphi }&0\\ {\sin \varphi }&{\rho \cos \varphi }&0\\ 0&0&1 \end{array}} \right| } ={ \rho \ge 0.} \] Тогда формула замены переменных при данном преобразовании имеет вид: \[ {\iiint\limits_U {f\left( {x,y,z} \right)dxdydz} } = {\iiint\limits_{U'} {f\left( {\rho \cos \varphi ,\rho \sin \varphi ,z} \right)\rho d\rho d\varphi dz} .} \] Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью.

   Пример 1

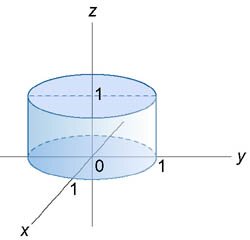
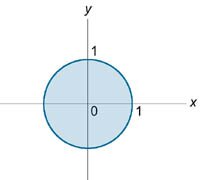
Вычислить интеграл \[\iiint\limits_U {\left( {{x^4} + 2{x^2}{y^2} + {y^4}} \right)dxdydz} ,\] где область \(U\) ограничена поверхностью \({x^2} + {y^2} \le 1\) и плоскостями \(z = 0,\) \(z = 1\) (рисунок \(2\)). Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость \(Oxy\) представляет собой круг \({x^2} + {y^2} \le 1\) или \(0 \le \rho \le 1\) (рисунок \(3\)).

Заметим, что подынтегральное выражение записывается в виде \[ {\left( {{x^4} + 2{x^2}{y^2} + {y^4}} \right) } = {{\left( {{x^2} + {y^2}} \right)^2} } = {{\left( {{\rho ^2}} \right)^2} = {\rho ^4}.} \] Тогда интеграл будет равен \[I = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}\rho d\rho } \int\limits_0^1 {dz} .\] Здесь во втором интеграле добавлен множитель \(\rho\) − якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга. В результате тройной интеграл легко вычисляется: \[ {I = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}\rho d\rho } \int\limits_0^1 {dz} } = {2\pi \int\limits_0^1 {{\rho ^5}d\rho } \int\limits_0^1 {dz} } = {2\pi \cdot 1 \cdot \int\limits_0^1 {{\rho ^5}d\rho } } = {2\pi \left. {\left( {\frac{{{\rho ^6}}}{6}} \right)} \right|_0^1 } = {2\pi \cdot \frac{1}{6} = \frac{\pi }{3}.} \]

   Пример 2

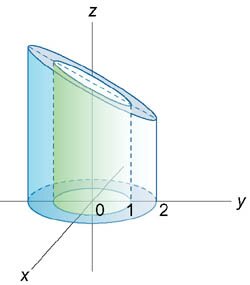
Вычислить интеграл \[\iiint\limits_U {\left( {{x^2} + {y^2}} \right)dxdydz} ,\] где область \(U\) ограничена поверхностями \({x^2} + {y^2} = 3z,\) \(z = 3\) (рисунок \(4\)). Область интегрирования изображена на рисунке \(4.\) Для вычисления интеграла перейдем к цилиндрическим координатам: \[ {x = \rho \cos \varphi ,}\;\; {y = \rho \sin \varphi ,}\;\; {z = z.} \] Дифференциал при этом равен \[dxdydz = \rho d\rho d\varphi dz\;\;\left( {\rho - \text{якобиан}} \right).\] Уравнение параболической поверхности принимает вид: \[{\rho ^2}{\cos ^2}\varphi + {\rho ^2}{\sin^2}\varphi = 3z\;\;\text{или}\;\;{\rho ^2} = 3z.\] Проекция области интегрирования \(U\) на плоскость \(Oxy\) представляет собой окружность \({x^2} + {y^2} \le 9\) радиусом \(\rho = 3\) (рисунок \(5\)). Координата \(\rho\) изменяется в пределах от \(0\) до \(3,\) угол \(\varphi\) − от \(0\) до \(2\pi\) и координата \(z\) − от \(\large\frac{{{\rho ^2}}}{3}\normalsize\) до \(3.\) В результате интеграл будет равен \[ {I = \iiint\limits_U {\left( {{x^2} + {y^2}} \right)dxdydz} } = {\iiint\limits_{U'} {{\rho ^2} \cdot \rho d\rho d\varphi dz} } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^3 {{\rho ^3}d\rho } \int\limits_{\frac{{{\rho ^2}}}{3}}^3 {dz} } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^3 {{\rho ^3}d\rho } \cdot \left[ {\left. z \right|_{\frac{{{\rho ^2}}}{3}}^3} \right] } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^3 {{\rho ^3}\left( {3 - \frac{{{\rho ^2}}}{3}} \right)d\rho } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^3 {\left( {3{\rho ^3} - \frac{{{\rho ^5}}}{3}} \right)d\rho } } = {\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{3{\rho ^4}}}{4} - \frac{{{\rho ^6}}}{{18}}} \right)} \right|_0^3} \right] } = {\left( {\frac{{3 \cdot 81}}{4} - \frac{{729}}{{18}}} \right)\int\limits_0^{2\pi } {d\varphi } } = {\frac{{81}}{4} \cdot 2\pi = \frac{{81\pi }}{2}.} \]

   Пример 3

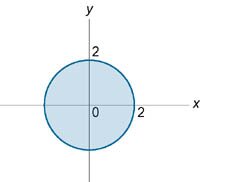
Используя цилиндрические координаты, найти значение интеграла \[ I = \int\limits_{ - 2}^2 {dx} \int\limits_{ - \sqrt {4 - {x^2}} }^{\sqrt {4 - {x^2}} } {dy} \int\limits_0^{4 - {x^2} - {y^2}} {{y^2}dz} .\] Область интегрирования \(U\) изображена на рисунке \(6.\) Ее проекция на плоскость \(Oxy\) представляет собой круг \({x^2} + {y^2} = {2^2}\) (рисунок \(7\)).

Новые переменные в цилиндрических координатах будут изменяться в пределах \[ {0 \le \rho \le 2,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {0 \le z \le 4 - {\rho ^2}.} \] Подставляя \(x = \rho \cos \varphi \) и \(x = \rho \sin \varphi,\) найдем значение интеграла: \[ {I = \int\limits_{ - 2}^2 {dx} \int\limits_{ - \sqrt {4 - {x^2}} }^{\sqrt {4 - {x^2}} } {dy} \int\limits_0^{4 - {x^2} - {y^2}} {{y^2}dz} } = {\iiint\limits_U {{y^2}dxdydz} } = {\iiint\limits_{U'} {{{\left( {\rho \sin \varphi } \right)}^2}\rho d\rho d\varphi dz} } = {\iiint\limits_{U'} {{\rho ^3}{{\sin }^2}\varphi d\rho d\varphi dz} } = {\int\limits_0^{2\pi } {{{\sin }^2}\varphi d\varphi } \int\limits_0^2 {{\rho ^3}\left( {4 - {\rho ^2}} \right)d\rho } } = {\int\limits_0^{2\pi } {{{\sin }^2}\varphi d\varphi } \int\limits_0^2 {\left( {4{\rho ^3} - {\rho ^5}} \right)d\rho } } = {\int\limits_0^{2\pi } {{{\sin }^2}\varphi d\varphi } \cdot \left[ {\left. {\left( {\frac{{4{\rho ^4}}}{4} - \frac{{{\rho ^6}}}{6}} \right)} \right|_0^2} \right] } = {\left( {{2^4} - \frac{{{2^6}}}{6}} \right)\int\limits_0^{2\pi } {{{\sin }^2}\varphi d\varphi } } = {\frac{{16}}{3}\int\limits_0^{2\pi } {{{\sin }^2}\varphi d\varphi } } = {\frac{{16}}{3}\int\limits_0^{2\pi } {\frac{{1 - \cos 2\varphi }}{2}d\varphi } } = {\frac{8}{3}\int\limits_0^{2\pi } {\left( {1 - \cos 2\varphi } \right)d\varphi } } = {\frac{8}{3}\left[ {\left. {\left( {\varphi - \frac{{\sin 2\varphi }}{2}} \right)} \right|_0^{2\pi }} \right] } = {\frac{8}{3} \cdot 2\pi = \frac{{16\pi }}{3}.} \]

   Пример 4

Вычислить интеграл, используя цилиндрические координаты: \[\iiint\limits_U {\sqrt {{x^2} + {y^2}} dxdydz} .\] Область \(U\) ограничена параболоидом \(z = 4 - {x^2} - {y^2},\) цилиндром \({x^2} + {y^2} = 4\) и плоскостями \(y = 0,\) \(z = 0\) (рисунок \(8\)). Изобразив схематически область интегрирования \(U,\) находим, что ее проекция на плоскость \(Oxy\) (область \(D\)) представляет собой полукруг радиусом \(\rho = 2\) (рисунок \(9\)).

Перейдем к цилиндрическим координатам, применяя подстановки \[ {x = \rho \cos \varphi ,}\;\; {y = \rho \sin \varphi ,}\;\; {z = z,}\;\; {dxdydz = \rho d\rho d\varphi dz.} \] Новые переменные будут изменяться в пределах \[ {0 \le \rho \le 2,}\;\; {0 \le \varphi \le \pi ,}\;\; {0 \le z \le 4 - {\rho ^2}.} \] Теперь вычисляем интеграл: \[ {I = \iiint\limits_U {\sqrt {{x^2} + {y^2}} dxdydz} } = {\iiint\limits_{U'} {\rho \cdot \rho d\rho d\varphi dz} } = {\iiint\limits_{U'} {{\rho ^2}d\rho d\varphi dz} } = {\int\limits_0^\pi {d\varphi } \int\limits_0^2 {{\rho ^2}d\rho } \int\limits_0^{4 - {\rho ^2}} {dz} } = {\int\limits_0^\pi {d\varphi } \int\limits_0^2 {{\rho ^2}d\rho } \cdot \left[ {\left. z \right|_0^{4 - {\rho ^2}}} \right] } = {\int\limits_0^\pi {d\varphi } \int\limits_0^2 {{\rho ^2}\left( {4 - {\rho ^2}} \right)d\rho } } = {\int\limits_0^\pi {d\varphi } \int\limits_0^2 {\left( {4{\rho ^2} - {\rho ^4}} \right)d\rho } } = {\int\limits_0^\pi {d\varphi } \left[ {\left. {\left( {\frac{{4{\rho ^3}}}{3} - \frac{{{\rho ^5}}}{5}} \right)} \right|_0^2} \right] } = {\left( {\frac{4}{3} \cdot {2^3} - \frac{{{2^5}}}{5}} \right)\int\limits_0^\pi {d\varphi } } = {\frac{{64}}{{15}}\int\limits_0^\pi {d\varphi } } = {\frac{{64}}{{15}} \cdot \left[ {\left. \varphi \right|_0^\pi } \right] = \frac{{64\pi }}{{15}}.} \]

   Пример 5

Найти интеграл \[\iiint\limits_U {ydxdydz},\] где область \(U\) ограничена плоскостями \(z = x + 1,\) \(z = 0\) и цилиндрическими поверхностями \({x^2} + {y^2} = 1,\) \({x^2} + {y^2} = 4\) (рисунок \(10\)). Вычислим данный интеграл в цилиндрических координатах. Из условия \[0 \le z \le x + 1\] следует, что \[0 \le z \le \rho \cos \varphi + 1.\] Область интегрирования в плоскости \(Oxy\) представляет собой кольцо, ограниченное окружностями \({x^2} + {y^2} = 1\) и \({x^2} + {y^2} = 4\) (рисунок \(11\)). Следовательно, переменные \(\rho\) и \(\varphi\) изменяются в интервале \[1 \le \rho \le 2,\;\;0 \le \varphi \le 2\pi .\] Находим интеграл: \[ {I = \iiint\limits_U {ydxdydz} } = {\iiint\limits_{U'} {\rho \sin \varphi \cdot \rho d\rho d\varphi dz} } = {\iiint\limits_{U'} {{\rho ^2}\sin \varphi d\rho d\varphi dz} } = {\int\limits_0^{2\pi } {\sin \varphi d\varphi } \int\limits_0^2 {{\rho ^2}d\rho } \int\limits_0^{\rho \cos \varphi + 1} {dz} } = {\int\limits_0^{2\pi } {\sin \varphi d\varphi } \int\limits_0^2 {{\rho ^2}d\rho } \cdot \left[ {\left. z \right|_0^{\rho \cos \varphi + 1}} \right] } = {\int\limits_0^{2\pi } {\sin \varphi d\varphi } \int\limits_0^2 {{\rho ^2}\left( {\rho \cos \varphi + 1} \right)d\rho } } = {\int\limits_0^{2\pi } {\sin \varphi d\varphi } \int\limits_0^2 {\left( {{\rho ^3}\cos \varphi + {\rho ^2}} \right)d\rho } } = {\int\limits_0^{2\pi } {\sin \varphi d\varphi } \cdot \left[ {\left. {\left( {\frac{{{\rho ^4}}}{4}\cos \varphi + \frac{{{\rho ^3}}}{3}} \right)} \right|_{\rho = 1}^{\rho = 2}} \right] } = {\int\limits_0^{2\pi } {\sin \varphi \left[ {\left( {4\cos \varphi + \frac{8}{3}} \right) - \left( {\frac{{\cos \varphi }}{4} + \frac{1}{3}} \right)} \right]d\varphi } } = {\int\limits_0^{2\pi } {\sin \varphi \left( {\frac{{15}}{4}\cos \varphi + \frac{7}{3}} \right)d\varphi } } = {\int\limits_0^{2\pi } {\left( {\frac{{15}}{4}\sin \varphi \cos \varphi + \frac{7}{3}\sin \varphi } \right)d\varphi } } = {\int\limits_0^{2\pi } {\left( {\frac{{15}}{8}\sin 2\varphi + \frac{7}{3}\sin \varphi } \right)d\varphi } } = {\left. {\left( { - \frac{{15}}{{16}}\cos 2\varphi - \frac{7}{3}\cos \varphi } \right)} \right|_0^{2\pi } = 0.} \] Этот результат закономерен, поскольку область \(U\) симметрична относительно плоскости \(Oxz,\) а подынтегральная функция является четной.