Тройные интегралы в сферических координатах

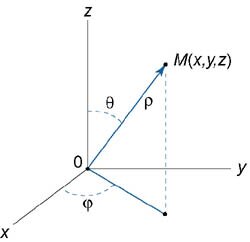
Сферическими координатами точки \(M\left( {x,y,z} \right)\) называются три числа − \(\rho, \varphi, \theta,\) где
Обратите внимание, что определения \(\rho,\) \(\varphi\) в сферических и цилиндрических координатах отличаются друг от друга.

Сферические координаты точки связаны с ее декартовыми координатами соотношениями \[ {x = \rho \cos \varphi \sin \theta ,}\;\; {y = \rho \sin \varphi \sin \theta ,}\;\; {z = \rho \cos \theta ,} \] \[ {\text{где}\;\;\rho \ge 0,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {0 \le \theta \le \pi .} \] Якобиан перехода от декартовых координат к сферическим имеет вид: \[ {I\left( {\rho ,\varphi ,\theta } \right) } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \rho }}}&{\frac{{\partial x}}{{\partial \varphi }}}&{\frac{{\partial x}}{{\partial \theta }}}\\ {\frac{{\partial y}}{{\partial \rho }}}&{\frac{{\partial y}}{{\partial \varphi }}}&{\frac{{\partial y}}{{\partial \theta }}}\\ {\frac{{\partial z}}{{\partial \rho }}}&{\frac{{\partial z}}{{\partial \varphi }}}&{\frac{{\partial z}}{{\partial \theta }}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\cos \varphi \sin \theta }&{ - \rho \sin \varphi \sin \theta }&{\rho \cos \varphi \cos \theta }\\ {\sin \varphi \sin \theta }&{\rho \cos \varphi \sin \theta }&{\rho \sin \varphi \cos \theta }\\ {\cos \theta }&0&{ - \rho \sin \theta } \end{array}} \right|.} \] Раскладывая определитель по второму столбцу, получаем \[ {I\left( {\rho ,\varphi ,\theta } \right) } = {\rho \sin \varphi \sin \theta \cdot \left| {\begin{array}{*{20}{c}} {\sin \varphi \sin \theta }&{\rho \sin \varphi \cos \theta }\\ {\cos \theta }&{ - \rho \sin \theta } \end{array}} \right| } + {\rho \cos \varphi \sin \theta \cdot \left| {\begin{array}{*{20}{c}} {\cos \varphi \sin \theta }&{\rho \cos \varphi \cos \theta }\\ {\cos \theta }&{ - \rho \sin \theta } \end{array}} \right| } = {\rho \sin \varphi \sin \theta \left( { - \rho \sin \varphi \,{{\sin }^2}\theta - \rho \sin \varphi \,{{\cos }^2}\theta } \right) } + {\rho \cos \varphi \sin \theta \left( { - \rho \cos \varphi \,{{\sin }^2}\theta - \rho \cos \varphi \,{{\cos }^2}\theta } \right) } = {\rho \sin \varphi \sin \theta \cdot \left( { - \rho \sin \varphi } \right) \cdot 1 } + {\rho \cos \varphi \sin \theta \cdot \left( { - \rho \cos \varphi } \right) \cdot 1 } = {- {\rho ^2}\sin \theta \left( {{{\sin }^2}\varphi + {{\cos }^2}\varphi } \right) } = { - {\rho ^2}\sin \theta .} \] Соответственно, абсолютное значение якобиана равно \[\left| {I\left( {\rho ,\varphi ,\theta } \right)} \right| = {\rho ^2}\sin \theta .\] Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид: \[ {\iiint\limits_U {f\left( {x,y,z} \right)dxdydz} } = {\iiint\limits_{U'} {f\left( {\rho \cos \varphi \sin \theta ,\rho \sin \varphi \sin \theta,\rho \cos \theta } \right){\rho ^2}\sin \theta d\rho d\varphi d\theta } .} \] Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования \(U\) представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид \(f\left( {{x^2} + {y^2} + {z^2}} \right).\)

Иногда выгодно использовать т.н. обобщенные сферические координаты, связанные с декартовыми формулами \[ {x = a\rho \cos \varphi \sin \theta ,}\;\; {y = b\rho \sin \varphi \sin \theta ,}\;\; {z = c\rho \cos \theta .} \] В этом случае якобиан равен \[I\left( {\rho ,\varphi ,\theta } \right) = - abc{\rho ^2}\sin \theta .\]

   Пример 1

Найти интеграл \(\iiint\limits_U {\sqrt {{x^2} + {y^2} + {z^2}} dxdydz},\) где область интегрирования \(U\) − шар, заданный уравнением \({{x^2} + {y^2} + {z^2}} = 25.\) Поскольку область \(U\) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от \(f\left( {{x^2} + {y^2} + {z^2}} \right),\) то перейдем к сферическим координатам. Сделаем замену: \[ {x = \rho \cos \varphi \sin \theta ,}\;\; {y = \rho \sin \varphi \sin \theta ,}\;\; {z = \rho \cos \theta ,} \] Новые переменные изменяются в пределах: \[ {0 \le \rho \le 5,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {0 \le \theta \le \pi .} \] Учитывая якобиан \({\rho ^2}\sin \theta,\) записываем интеграл в виде: \[ {I = \iiint\limits_U {\sqrt {{x^2} + {y^2} + {z^2}} dxdydz} } = {\iiint\limits_{U'} {\rho \cdot {\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^5 {{\rho ^3}d\rho } \int\limits_0^\pi {\sin \theta d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^5 {{\rho ^3}d\rho } \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^5 {{\rho ^3}d\rho } \left( { - \cos \pi + \cos 0} \right) } = {2\int\limits_0^{2\pi } {d\varphi } \int\limits_0^5 {{\rho ^3}d\rho } } = {2\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{\rho ^4}}}{4}} \right)} \right|_0^5} \right] } = {2\int\limits_0^{2\pi } {d\varphi } \cdot \frac{{{5^4}}}{4} } = {\frac{{625}}{2}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{625}}{2} \cdot 2\pi = 625\pi .} \]

   Пример 2

Вычислить интеграл \[\iiint\limits_U {{e^{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^{\frac{3}{2}}}}}dxdydz} ,\] где область \(U\) представляет собой единичный шар \({{x^2} + {y^2} + {z^2}} \le 1.\) Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования \(U\) описывается неравенствами \[ {0 \le \rho \le 1,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {0 \le \theta \le \pi .} \] Записывая интеграл в сферических координатах, получаем \[ {I = \iiint\limits_U {{e^{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^{\frac{3}{2}}}}}dxdydz} } = {\iiint\limits_{U'} {{e^{{{\left( {{\rho ^2}} \right)}^{\frac{3}{2}}}}}{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\iiint\limits_{U'} {{e^{{\rho ^3}}}{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{e^{{\rho ^3}}}{\rho ^2}d\rho } \int\limits_0^\pi {\sin \theta d\theta } .} \] Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим \[ {I = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{e^{{\rho ^3}}}{\rho ^2}d\rho } \int\limits_0^\pi {\sin \theta d\theta } } = {\left[ {\left. \varphi \right|_0^{2\pi }} \right] \cdot \int\limits_0^1 {\left( {{e^{{\rho ^3}}} \cdot \frac{1}{3}d{\rho ^3}} \right)} \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] } = {2\pi \cdot \frac{1}{3}\left[ {\left. {\left( {{e^{{\rho ^3}}}} \right)} \right|_{{\rho ^3} = 0}^{{\rho ^3} = 1}} \right] \cdot \left( { - \cos \pi + \cos 0} \right) } = {\frac{{2\pi }}{3} \cdot \left( {e - 1} \right) \cdot 2 } = {\frac{{4\pi }}{3}\left( {e - 1} \right).} \]

   Пример 3

Вычислить интеграл \(\iiint\limits_U {xyzdxdydz} ,\) где область \(U\) представляет собой часть шара \({x^2} + {y^2} + {z^2} \le {R^2},\) расположенную в первом октанте \(x \ge 0, y \ge 0, z \ge 0.\) Перейдем к сферическим координатам. Сделаем замену переменных: \[ {x = \rho \cos \varphi \sin \theta ,}\;\; {y = \rho \sin \varphi \sin \theta ,}\;\; {z = \rho \cos \theta ,}\;\; {dxdydz = {\rho ^2}\sin \theta d\rho d\varphi d\theta .} \] Новые переменные будут изменяться в пределах: \[ {0 \le \rho \le R,}\;\; {0 \le \varphi \le \frac{\pi }{2},}\;\;0 {\le \theta \le \frac{\pi }{2}.} \] Тогда интеграл в сферических координатах равен \[ {I = \iiint\limits_U {xyzdxdydz} } = {\iiint\limits_{U'} {\left[ {\rho \cos \varphi \sin \theta \cdot \rho \sin \varphi \sin \theta \cdot \rho \cos \theta \cdot {\rho ^2}\sin \theta d\rho d\varphi d\theta } \right]} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos \varphi \sin \varphi d\varphi } \int\limits_0^R {{\rho ^5}d\rho } \int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\sin }^3}\theta \cos \theta d\theta } } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\frac{1}{2}\sin 2\varphi d\varphi } \right)} \int\limits_0^R {{\rho ^5}d\rho } \int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\sin }^3}\theta \cos \theta d\theta } } = {\frac{1}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2\varphi d\varphi } \int\limits_0^R {{\rho ^5}d\rho } \int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\sin }^3}\theta d\left( {\sin \theta } \right)} } = {\frac{1}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2\varphi d\varphi } \int\limits_0^R {{\rho ^5}d\rho } \cdot \left[ {\left. {\left( {\frac{{{{\sin }^4}\theta }}{4}} \right)} \right|_{\theta = 0}^{\theta = \large\frac{\pi }{2}\normalsize}} \right] } = {\frac{1}{8}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2\varphi d\varphi } \int\limits_0^R {{\rho ^5}d\rho } \cdot \left( {{{\sin }^4}\frac{\pi }{2} - {{\sin }^4}0} \right) } = {\frac{1}{8}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2\varphi d\varphi } \int\limits_0^R {{\rho ^5}d\rho } \cdot 1 } = {\frac{1}{8}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2\varphi d\varphi } \cdot \left[ {\left. {\left( {\frac{{{\rho ^6}}}{6}} \right)} \right|_0^R} \right] } = {\frac{{{R^6}}}{{48}}\left[ {\left. {\left( { - \frac{{\cos 2\varphi }}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{{{R^6}}}{{96}}\left( { - \cos \pi + \cos 0} \right) } = {\frac{{{R^6}}}{{96}} \cdot 2 } = {\frac{{{R^6}}}{{48}}.} \]

   Пример 4

Найти тройной интеграл \[\iiint\limits_U {\left( {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}}} \right)dxdydz} ,\] где область \(U\) ограничена эллипсоидом \[{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}}} = 1.\] Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: \[ {x = a\rho \cos \varphi \sin \theta ,}\;\; {y = b\rho \sin \varphi \sin \theta ,}\;\; {z = c\rho \cos \theta .} \] Модуль якобиана данного преобразования равен \(\left| I \right| = abc{\rho ^2}\sin \theta .\) Поэтому для дифференциалов справедливо соотношение \[dxdydz = abc{\rho ^2}\sin \theta d\rho d\varphi d\theta .\] В новых координатах интеграл принимает вид: \[ {I = \iiint\limits_U {\left( {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}}} \right)dxdydz} } = {\iiint\limits_{U'} {\left[ {\frac{{{{\left( {a\rho \cos \varphi \sin \theta } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {b\rho \sin \varphi \sin \theta } \right)}^2}}}{{{b^2}}} + \frac{{{{\left( {c\rho \cos \theta } \right)}^2}}}{{{c^2}}}} \right]abc{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\iiint\limits_{U'} {\left[ {{\rho ^2}{{\cos }^2}\varphi \,{{\sin }^2}\theta + {\rho ^2}{\sin^2}\varphi \,{{\sin }^2}\theta + {\rho ^2}{{\cos }^2}\theta } \right]abc{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\iiint\limits_{U'} {\left[ {{\rho ^2}{{\sin }^2}\theta \underbrace {\left( {{{\cos }^2}\varphi + {\sin^2}\varphi } \right)}_1 + {\rho ^2}{{\cos }^2}\theta } \right]abc{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {\iiint\limits_{U'} {{\rho ^2}\underbrace {\left( {{\sin^2}\theta + {{\cos }^2}\theta } \right)}_1abc{\rho ^2}\sin \theta d\rho d\varphi d\theta } } = {abc\iiint\limits_{U'} {{\rho ^4}\sin \theta d\rho d\varphi d\theta } .} \] Область интегрирования \(U'\) в сферических координатах представляет собой параллелепипед и определяется неравенствами \[ {0 \le \rho \le 1,}\;\; {0 \le \varphi \le 2\pi ,}\;\; {0 \le \theta \le \pi .} \] Тогда тройной интеграл становится равным \[ {I = abc\iiint\limits_{U'} {{\rho ^4}\sin \theta d\rho d\varphi d\theta } } = {abc\int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}d\rho } \int\limits_0^\pi {\sin \theta d\theta } } = {abc\int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}d\rho } \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] } = {abc\int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}d\rho } \cdot \left( { - \cos \pi + \cos 0} \right) } = {2abc\int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{\rho ^4}d\rho } } = {2abc\int\limits_0^{2\pi } {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{\rho ^5}}}{5}} \right)} \right|_0^1} \right] } = {\frac{{2abc}}{5}\int\limits_0^{2\pi } {d\varphi } } = {\frac{{2abc}}{5} \cdot \left[ {\left. \varphi \right|_0^{2\pi }} \right] } = {\frac{{2abc}}{5} \cdot 2\pi = \frac{{4abc\pi }}{5}.} \]

   Пример 5

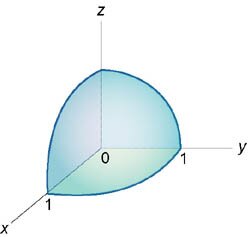
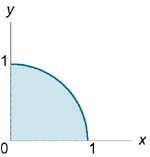
Вычислить интеграл \[\int\limits_0^1 {dx} \int\limits_0^{\sqrt {1 - {x^2}} } {dy} \int\limits_0^{\sqrt {1 - {x^2} - {y^2}} } {{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}dz} ,\] используя сферические координаты. Область интегрирования представляет собой часть шара, расположенная в первом октанте (рисунки \(2,3\)) и, следовательно, ограничена неравенствами \[ {0 \le \rho \le 1,}\;\; {0 \le \varphi \le \frac{\pi }{2},}\;\; {0 \le \theta \le \frac{\pi }{2}.} \] Учитывая, что подынтегральное выражение равно \[ {{\left( {{x^2} + {y^2} + {z^2}} \right)^2} } = {{\left[ {{{\left( {\rho \cos \varphi \sin \theta } \right)}^2} + {{\left( {\rho \sin \varphi \sin \theta } \right)}^2} + {{\left( {\rho \cos \theta } \right)}^2}} \right]^2} } = {{\left[ {{\rho ^2}{{\cos }^2}\varphi \,{{\sin }^2}\theta + {\rho ^2}{\sin^2}\varphi \,{{\sin }^2}\theta + {\rho ^2}{{\cos }^2}\theta } \right]^2} } = {{\left[ {{\rho ^2}{{\sin }^2}\theta \underbrace {\left( {{{\cos }^2}\varphi + {\sin^2}\varphi } \right)}_1 + {\rho ^2}{{\cos }^2}\theta } \right]^2} } = {{\left[ {{\rho ^2}{{\sin }^2}\theta + {\rho ^2}{{\cos }^2}\theta } \right]^2} } = {{\left[ {{\rho ^2}\underbrace {\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right)}_1} \right]^2} } = {{\rho ^4},} \] а дифференциалы связаны соотношениями \[dxdydz = {\rho ^2}\sin \theta d\rho d\varphi d\theta ,\] получаем \[ {I = \int\limits_0^1 {dx} \int\limits_0^{\sqrt {1 - {x^2}} } {dy} \int\limits_0^{\sqrt {1 - {x^2} - {y^2}} } {{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}dz} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } \int\limits_0^1 {\left( {{\rho ^4} \cdot {\rho ^2}d\rho } \right)} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin \theta d\theta } } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } \int\limits_0^1 {{\rho ^6}d\rho } \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } \int\limits_0^1 {{\rho ^6}d\rho } \cdot \left( { - \cos \frac{\pi }{2} + \cos 0} \right) } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } \int\limits_0^1 {{\rho ^6}d\rho } \cdot 1 } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } \cdot \left[ {\left. {\left( {\frac{{{\rho ^7}}}{7}} \right)} \right|_0^1} \right] } = {\frac{1}{7}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\varphi } } = {\frac{1}{7} \cdot \left[ {\left. \varphi \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{1}{7} \cdot \frac{\pi }{2} } = {\frac{\pi }{{14}}.} \]