Соприкосновение плоских кривых

Пусть на плоскости заданы две кривые \(y = f\left( x \right)\) и \(y = g\left( x \right),\) которые касаются в точке \({M_0}\left( {{x_0},{y_0}} \right)\) (рисунок \(1\)) и имеют производные до \(\left( {n + 1} \right)\)-го порядка включительно. Говорят, что кривые \(y = f\left( x \right)\) и \(y = g\left( x \right)\) имеют в точке \({M_0}\left( {{x_0},{y_0}} \right)\) касание \(n\)-го порядка, если выполняются следующие условия: \[ {f\left( {{x_0}} \right) = g\left( {{x_0}} \right),}\;\; {f'\left( {{x_0}} \right) = g'\left( {{x_0}} \right),}\;\; {f''\left( {{x_0}} \right) = g''\left( {{x_0}} \right),\;\ldots,\;} {{f^{\left( n \right)}}\left( {{x_0}} \right) = {g^{\left( n \right)}}\left( {{x_0}} \right),}\;\; {{f^{\left( {n + 1} \right)}}\left( {{x_0}} \right) \ne {g^{\left( {n + 1} \right)}}\left( {{x_0}} \right).} \] В частности, если \(n = 1,\) то кривые \(y = f\left( x \right)\) и \(y = g\left( x \right)\) имеют общую касательную.

Случай \(n = 0\) означает, что кривые имеют общую точку \({M_0}\left( {{x_0},{y_0}} \right):\) \(f\left( {{x_0}} \right) = g\left( {{x_0}} \right),\) но их первые производные при этом не совпадают: \(f'\left( {{x_0}} \right) \ne g'\left( {{x_0}} \right).\) В этом случае кривые просто пересекаются в точке \({M_0}.\)

Можно рассмотреть разность функций \(\varphi \left( x \right) = g\left( x \right) - f\left( x \right)\) в окрестности точки \({x_0}\) и разложить ее в ряд Тейлора с остаточным членом в форме Пеано. Если кривые \(g\left( x \right)\) и \(f\left( x \right)\) имеют порядок касания \(n,\) то первые \(n\) членов ряда равны нулю и разность \(\varphi \left( x \right)\) представляется в виде \[ {\varphi \left( x \right) = \frac{{{\varphi ^{\left( {n + 1} \right)}}\left( {{x_0}} \right) + \alpha }}{{\left( {n + 1} \right)!}}{\left( {x - {x_0}} \right)^{n + 1}} } = {\frac{{{g^{\left( {n + 1} \right)}}\left( {{x_0}} \right) - {f^{\left( {n + 1} \right)}}\left( {{x_0}} \right) + \alpha }}{{\left( {n + 1} \right)!}}{\left( {x - {x_0}} \right)^{n + 1}},} \] т.е. пропорциональна \({\left( {x - {x_0}} \right)^{n + 1}}.\) Следовательно, при четном значении \(n\) разность \(\varphi \left( x \right)\) имеет разные знаки слева и справа от точки касания \({x_0},\) т.е. в этом случае кривые пересекаются в точке \({M_0}.\) Частный случай \(n = 0\) рассмотрен выше.

При нечетном \(n\) кривые \(y = f\left( x \right)\) и \(y = g\left( x \right)\) касаются друг друга в точке \({M_0}\) без взаимного пересечения. Рассмотрим следующую задачу. Дано уравнение кривой \(y = f\left( x \right)\) и семейство кривых \[G\left( {x,y,a,b, \ldots ,\ell} \right) = 0\] с \(n + 1\) параметрами \({a,b, \ldots ,\ell}.\) Требуется, изменяя значения параметров, выбрать из данного семейства такую кривую, которая с кривой \(y = f\left( x \right)\) в точке \({M_0}\left( {{x_0},{y_0}} \right)\) имела бы наивысший возможный порядок касания. Такая кривая будет называться соприкасающейся кривой.

Введем обозначение \[\Phi \left( {x,a,b, \ldots ,l} \right) = G\left( {x,f\left( x \right),a,b, \ldots ,l} \right).\] Условия касания записываются в виде: \[\left\{ \begin{array}{l} \Phi \left( {{x_0},a,b, \ldots ,\ell} \right) = 0\\ {\Phi'_x}\left( {{x_0},a,b, \ldots ,\ell} \right) = 0\\ {\Phi''_{xx}}\left( {{x_0},a,b, \ldots ,\ell} \right) = 0\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ \Phi _{{x^n}}^{\left( n \right)}\left( {{x_0},a,b, \ldots ,\ell} \right) = 0 \end{array} \right..\] В результате мы получаем систему из \(n + 1\) уравнений с \(n + 1\) неизвестными значениями параметров. Решая эту систему, находим параметры \({a,b, \ldots ,\ell}\) и уравнение соприкасающейся кривой. Обычно ее порядок касания будет не ниже, чем \(n\) (в случае \(n + 1\) параметров). Таким образом, порядок касания соприкасающейся кривой, как правило, на единицу меньше числа параметров. Выведем уравнение соприкасающейся окружности. Пусть задана функция \(y = f\left( x \right),\) которая является по меньшей мере дважды дифференцируемой. Семейство окружностей описывается уравнением \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\] Как видно, здесь мы имеем дело с тремя параметрами − координатами центра окружности \(a, b\) и ее радиусом \(R.\) Ясно, что в данном случае максимально возможный порядок касания равен \(2.\)

Обозначив \[\Phi \left( {x,a,b,R} \right) = {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} - {R^2},\] запишем производные функции \(\Phi:\) \[ {{\Phi '_x}\left( {{x_0},a,b,R} \right) = 2\left( {x - a} \right) + 2\left( {y - b} \right)y',}\;\;\; {{\Phi ''_{xx}}\left( {{x_0},a,b,R} \right) = 2 + 2{\left( {y'} \right)^2} + 2\left( {y - b} \right)y''.} \] Полагая, что касание кривых происходит в точке \(\left( {{x_0},{y_0}} \right),\) получаем следующую систему трех уравнений для определения соприкасающейся окружности: \[ {\left\{ \begin{array}{l} \Phi \left( {{x_0},a,b,R} \right) = 0\\ {\Phi'_x}\left( {{x_0},a,b,R} \right) = 0\\ {\Phi''_{xx}}\left( {{x_0},a,b,R} \right) = 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {\left( {{x_0} - a} \right)^2} + {\left( {{y_0} - b} \right)^2} - {R^2} = 0\\ 2\left( {{x_0} - a} \right) + 2\left( {{y_0} - b} \right){y'_0} = 0\\ 2 + 2\left( {{y'_0}} \right)^2 + 2\left( {{y_0} - b} \right){y''_0} = 0 \end{array} \right..} \] Из последнего уравнения находим значение \(b:\) \[ {2 + 2{\left( {{y'_0}} \right)^2} + 2\left( {{y_0} - b} \right){y''_0} = 0,}\;\; {\Rightarrow \left( {{y_0} - b} \right){y''_0} = - 1 - {\left( {{y'_0}} \right)^2},}\;\; {\Rightarrow {y_0} - b = - \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}},}\;\; {\Rightarrow b = {y_0} + \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}.} \] Подставляя \({{y_0} - b}\) во второе уравнение, получаем координату \(a\) центра окружности: \[ {2\left( {{x_0} - a} \right) + 2\left( {{y_0} - b} \right){y'_0} = 0,}\;\; {\Rightarrow {x_0} - a = - \left( {{y_0} - b} \right){y'_0},}\;\; {\Rightarrow {x_0} - a = \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}{y'_0},}\;\; {\Rightarrow a = {x_0} - \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}{y'_0}.} \] Радиус соприкасающейся окружности определяется из первого уравнения системы: \[ {{\left( {{x_0} - a} \right)^2} + {\left( {{y_0} - b} \right)^2} - {R^2} = 0,}\;\; {\Rightarrow {R^2} = {\left( {{x_0} - a} \right)^2} + {\left( {{y_0} - b} \right)^2},}\;\; {\Rightarrow {R^2} = {\left( {\frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}{y'_0}} \right)^2} + {\left( {\frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}} \right)^2},}\;\; {\Rightarrow {R^2} = {\left( {\frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}} \right)^2}\left[ {{{\left( {{y'_0}} \right)}^2} + 1} \right],}\;\; {\Rightarrow {R^2} = \frac{{{{\left[ {1 + {{\left( {{y'_0}} \right)}^2}} \right]}^3}}}{{{{\left( {{y''_0}} \right)}^2}}},}\;\; {\Rightarrow R = \frac{{{{\left[ {1 + {{\left( {{y'_0}} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{\left| {{y''_0}} \right|}}.} \] Как видно, координаты центра окружности \(a, b\) являются координатами центра кривизны кривой \(y = f\left( x \right)\) в точке \({x_0},\) а радиус соприкасающейся окружности совпадает со значением радиуса кривизны этой кривой в точке касания.

   Пример 1

Составить уравнение параболы, соприкасающейся с экспоненциальной функцией \(f\left( x \right) = {e^x}\) в точке \({x_0} = 0.\) Будем считать, что парабола задана уравнением \(y = g\left( x \right) = a{x^2} + bx + c.\) Данная функция содержит \(3\) параметра. Поэтому можно предположить, что порядок касания кривых равен \(2.\) Тогда коэффициенты \(a, b, c\) находятся из следующих условий: \[\left\{ \begin{array}{l} f\left( {{x_0}} \right) = g\left( {{x_0}} \right)\\ f'\left( {{x_0}} \right) = g'\left( {{x_0}} \right)\\ f''\left( {{x_0}} \right) = g''\left( {{x_0}} \right) \end{array} \right..\] Производные функций \(f\left( x \right) = {e^x}\) и \(g\left( x \right) = a{x^2} + bx + c\) выражаются формулами \[ {f'\left( x \right) = {\left( {{e^x}} \right)^\prime } = {e^x},}\;\;\; {f''\left( x \right) = {\left( {{e^x}} \right)^\prime } = {e^x};} \] \[ {g'\left( x \right) = {\left( {a{x^2} + bx + c} \right)^\prime } = 2ax + b,}\;\;\; {g''\left( x \right) = {\left( {2ax + b} \right)^\prime } = 2a.} \] Тогда система уравнений принимает такой вид: \[\left\{ \begin{array}{l} {e^{{x_0}}} = ax_0^2 + b{x_0} + c\\ {e^{{x_0}}} = 2a{x_0} + b\\ {e^{{x_0}}} = 2a \end{array} \right..\] Подставляя \({x_0} = 0,\) получаем: \[ \left\{ \begin{array}{l} c = 1\\ b = 1\\ 2a = 1 \end{array} \right. \;\;\text{или}\;\; \left\{ \begin{array}{l} a = \frac{1}{2}\\ b = 1\\ c = 1 \end{array} \right.. \] Итак, парабола, соприкасающаяся с экспоненциальной функцией в точке \({x_0} = 0,\) имеет второй порядок касания и определяется формулой \[y = \frac{{{x^2}}}{2} + x + 1.\] Если записать ее уравнение в виде \[ {y = \frac{{{x^2}}}{2} + x + 1 } = {\frac{1}{2}\left( {{x^2} + 2x} \right) + 1 } = {\frac{1}{2}\left( {{x^2} + 2x + 1 - 1} \right) + 1 } = {\frac{1}{2}{\left( {x + 1} \right)^2} + \frac{1}{2},} \] то видно, что вершина параболы находится в точке \(\left( { - 1,\large\frac{1}{2}\normalsize} \right).\) Схематически обе соприкасающиеся кривые показаны на рисунке \(2.\)

   Пример 2

Составить уравнение параболы, соприкасающейся с функцией \(f\left( x \right) = \cos x\) в точке \({x_0} = 0.\) Полагая, что семейство парабол является трехпараметрическим, т.е. описывается уравнением \[y = a{x^2} + bx + c\] с тремя параметрами \(a, b\) и \(c,\) введем функцию \[\Phi \left( {x,a,b,c} \right) = a{x^2} + bx + c - f\left( x \right)\] и запишем условие касания в точке \({x_0}\) в виде \[\left\{ \begin{array}{l} \Phi \left( {{x_0},a,b,c} \right) = 0\\ {\Phi '_x}\left( {{x_0},a,b,c} \right) = 0\\ {\Phi ''_{xx}}\left( {{x_0},a,b,c} \right) = 0 \end{array} \right..\] В нашем случае \(f\left( x \right) = \cos x.\) Следовательно, \[ {f'\left( x \right) = {\left( {\cos x} \right)^\prime } = - \sin x,}\;\;\; {f''\left( x \right) = {\left( { - \sin x} \right)^\prime } = - \cos x.} \] В результате имеем следующую систему для определения коэффициентов \(a, b, c:\) \[\left\{ \begin{array}{l} ax_0^2 + b{x_0} + c - \cos {x_0} = 0\\ 2a{x_0} + b + \sin {x_0} = 0\\ 2a + \cos {x_0} = 0 \end{array} \right..\] Подставляя \({x_0} = 0,\) получаем: \[\left\{ \begin{array}{l} c - 1 = 0\\ b = 0\\ 2a + 1 = 0 \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} a = - \frac{1}{2}\\ b = 0\\ c = 1 \end{array} \right..\] Таким образом, парабола, соприкасающаяся с функцией косинус в точке \({x_0} = 0,\) описывается уравнением \[y = - \frac{{{x^2}}}{2} + 1.\] Как видно, это уравнение соответствует первым двум членам разложения косинуса в ряд Маклорена.

   Пример 3

Найти уравнение кривой вида \[y = g\left( x \right) = \frac{a}{{x + b}},\] которая соприкасается с графиком функции \(f\left( x \right) = \ln x + 1\) в точке \({x_0} = 1.\) Семейство кривых \(g\left( x \right)\) содержит два параметра \(a\) и \(b.\) Поэтому касание данных кривых будет иметь первый порядок. Условия касания записываются следующим образом: \[\left\{ \begin{array}{l} f\left( {{x_0}} \right) = g\left( {{x_0}} \right)\\ f'\left( {{x_0}} \right) = g'\left( {{x_0}} \right) \end{array} \right..\] Здесь производные имеют вид: \[ {f'\left( x \right) = {\left( {\ln x + 1} \right)^\prime } = \frac{1}{x},}\;\;\; {g'\left( x \right) = {\left( {\frac{a}{{x + b}}} \right)^\prime } = - \frac{a}{{{{\left( {x + b} \right)}^2}}}.} \] Подставляя в систему выражения для функций и их производных, получаем: \[\left\{ \begin{array}{l} \ln {x_0} + 1 = \frac{a}{{{x_0} + b}}\\ \frac{1}{{{x_0}}} = - \frac{a}{{{{\left( {x + b} \right)}^2}}} \end{array} \right..\] Учитывая, что \({x_0} = 1,\) находим значения \(a\) и \(b:\) \[ {\left\{ \begin{array}{l} \ln 1 + 1 = \frac{a}{{1 + b}}\\ \frac{1}{1} = - \frac{a}{{{{\left( {1 + b} \right)}^2}}} \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} a = 1 + b\\ a = - \left( {1 + b} \right) \end{array} \right.,}\;\; {\Rightarrow a = - {a^2},}\;\; {\Rightarrow a + {a^2} = 0,}\;\; {\Rightarrow a\left( {1 + a} \right) = 0.} \] Содержательным решением является корень \(a = -1.\) Ему соответствует \(b = -2.\) Таким образом, дробно-рациональная функция, которая имеет касание \(1\)-го порядка (т.е. общую касательную) с кривой \(f\left( x \right) = \ln x + 1\) в точке \({x_0} = 1\) имеет такой вид: \[y = g\left( x \right) = - \frac{1}{{x - 2}} = \frac{1}{{2 - x}}.\]

   Пример 4

Составить уравнение кубической функции \[y = g\left( x \right) = a{x^3} + b{x^2} + cx + d,\] график которой соприкасается с кривой \(f\left( x \right) = \tan x\) в точке \({x_0} = 0.\) Здесь мы имеем дело с семейством функций, содержащих \(4\) параметра. Следовательно, наивысший возможный порядок касания кривых равен \(3.\) Для определения коэфициентов \(a, b, c\) и \(d\) запишем следующие условия касания: \[\left\{ \begin{array}{l} f\left( {{x_0}} \right) = g\left( {{x_0}} \right)\\ f'\left( {{x_0}} \right) = g'\left( {{x_0}} \right)\\ f''\left( {{x_0}} \right) = g''\left( {{x_0}} \right)\\ f'''\left( {{x_0}} \right) = g'''\left( {{x_0}} \right) \end{array} \right..\] Производные кубической функции имеют такой вид: \[g'\left( x \right) = {\left( {a{x^3} + b{x^2} + cx + d} \right)^\prime } = 3a{x^2} + 2bx + c,\] \[g''\left( x \right) = {\left( {3a{x^2} + 2bx + c} \right)^\prime } = 6ax + 2b,\] \[g'''\left( x \right) = {\left( {6ax + 2b} \right)^\prime } = 6a.\] Вычислим производные тангенса: \[f'\left( x \right) = {\left( {\tan x} \right)^\prime } = \frac{1}{{{{\cos }^2}x}},\] \[ {f''\left( x \right) = {\left( {\frac{1}{{{{\cos }^2}x}}} \right)^\prime } } = {{\left[ {{{\left( {\cos x} \right)}^{ - 2}}} \right]^\prime } } = { - 2{\left( {\cos x} \right)^{ - 3}} \cdot \left( { - \sin x} \right) } = {\frac{{2\sin x}}{{{{\cos }^3}x}},} \] \[ {f'''\left( x \right) = {\left( {\frac{{2\sin x}}{{{{\cos }^3}x}}} \right)^\prime } } = {\frac{{{{\left( {2\sin x} \right)}^\prime }{{\cos }^3}x - 2\sin x{{\left( {{{\cos }^3}x} \right)}^\prime }}}{{{{\cos }^6}x}} } = {\frac{{2\,\cos x\,{{\cos }^3}x - 2\sin x \cdot 3\,{{\cos }^2}x \cdot \left( { - \sin x} \right)}}{{{{\cos }^6}x}} } = {\frac{{2\,{{\cos }^3}x + 6\,{{\sin }^2}x\,{{\cos }^2}x}}{{{{\cos }^6}x}} } = {\frac{{{{\cos }^2}x\left( {2\,{{\cos }^2}x + 2\,{{\sin }^2}x + 4\,{{\sin }^2}x} \right)}}{{{{\cos }^6}x}} } = {\frac{{2 + 4\,{{\sin }^2}x}}{{{{\cos }^4}x}}.} \] Тогда система уравнений принимает вид: \[\left\{ \begin{array}{l} \tan {x_0} = ax_0^3 + bx_0^2 + c{x_0} + d\\ \frac{1}{{{{\cos }^2}{x_0}}} = 3ax_0^2 + 2b{x_0} + c\\ \frac{{2\sin {x_0}}}{{{{\cos }^3}{x_0}}} = 6a{x_0} + 2b\\ \frac{{2 + 4{{\sin }^2}{x_0}}}{{{{\cos }^4}{x_0}}} = 6a \end{array} \right..\] Подставляя значение \({x_0} = 0,\) получаем: \[\left\{ \begin{array}{l} d = 0\\ c = 1\\ 2b = 0\\ 6a = 2 \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} a = \frac{1}{3}\\ b = 0\\ c = 1\\ d = 0 \end{array} \right..\] Таким образом, соприкасающаяся кубическая функция записывается как \[y = \frac{{{x^3}}}{3} + x.\] Данная кривая имеет третий порядок касания с кривой тангенса в начале координат.

Заметим, что найденная кубическая функция представляет собой разложение тангенса в ряд Маклорена до третьего порядка.

   Пример 5

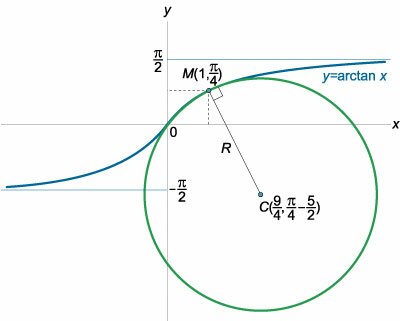
Составить уравнение окружности, соприкасаюшейся с кривой \(f\left( x \right) = \arctan x\) в точке \({x_0} = 1.\) Очевидно, что точка касания двух кривых имеет координаты \[\left( {{x_0},{y_0}} \right) = \left( {1,\frac{\pi }{4}} \right).\] Координаты центра соприкасающейся окружности и ее радиус находятся по формулам \[ {a = {x_0} - \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}{y'_0},}\;\;\; {b = {y_0} + \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}},}\;\;\; {R = \frac{{{{\left[ {1 + {{\left( {{y'_0}} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{\left| {{y''_0}} \right|}}.} \] Найдем производные, входящие в эти выражения: \[ {y' = {\left( {\arctan x} \right)^\prime } = \frac{1}{{1 + {x^2}}},}\;\;\; {y'' = {\left( {\frac{1}{{1 + {x^2}}}} \right)^\prime } = - \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}}.} \] Их значения при \({x_0} = 1\) составляют \[ {{y'_0} = y'\left( 1 \right) = \frac{1}{2},}\;\;\; {{y''_0} = y''\left( 1 \right) = - \frac{1}{2}.} \] Тогда координаты центра окружности равны \[ {a = {x_0} - \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}}{y'_0} } = {1 - \frac{{1 + {{\left( {\frac{1}{2}} \right)}^2}}}{{\left( { - \frac{1}{2}} \right)}} \cdot \frac{1}{2} } = {\frac{9}{4} = 2,25;} \] \[ {b = {y_0} + \frac{{1 + {{\left( {{y'_0}} \right)}^2}}}{{{y''_0}}} } = {\frac{\pi }{4} + \frac{{1 + {{\left( {\frac{1}{2}} \right)}^2}}}{{\left( { - \frac{1}{2}} \right)}} } = {\frac{\pi }{4} - \frac{5}{2} \approx - 1,71.} \] Вычислим также радиус соприкасающейся окружности: \[ {R = \frac{{{{\left[ {1 + {{\left( {{y'_0}} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{\left| {{y''_0}} \right|}} } = {\frac{{{{\left[ {1 + {{\left( {\frac{1}{2}} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{\left| { - \frac{1}{2}} \right|}} } = {\frac{{{{\left( {1 + \frac{1}{4}} \right)}^{\large\frac{3}{2}\normalsize}}}}{{\frac{1}{2}}} } = {2{\left( {\frac{5}{4}} \right)^{\large\frac{3}{2}\normalsize}} } = {\frac{{\sqrt {125} }}{4} \approx 2,80.} \] Таким образом, центр соприкасающейся окружности находится в точке \(\left( {\large\frac{9}{4}\normalsize,\large\frac{\pi }{4}\normalsize - \large\frac{5}{2}\normalsize} \right)\) (рисунок \(3\)).