Прогиб балки

Балкой называют конструктивный элемент, способный выдерживать большие нагрузки на изгиб. В случае малых прогибов форму балки можно описать линейным дифференциальным уравнением \(4\)-го порядка.

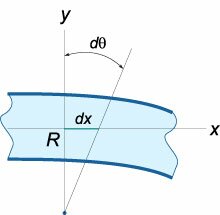
Рассмотрим вывод данного уравнения. При изгибе балки между двумя смежными сечениями, отстоящими друг от друга на расстоянии \(dx,\) образуется угол \(d\theta\) (рисунок \(1\)). При этом деформация \(\varepsilon \) в каждой точке будет пропорциональна координате \(y,\) которую будем отсчитывать от нейтральной линии. Длина нейтральной линии считается неизменной.

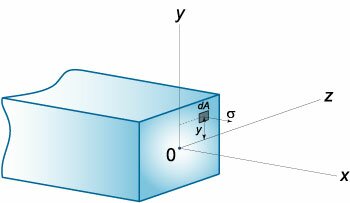
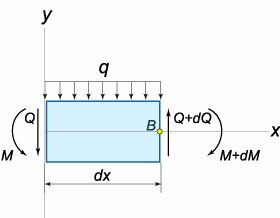
Из геометрии рисунка \(1\) следует, что \[\varepsilon = \frac{y}{R},\] где \(R\) − радиус кривизны бруса.

Величина нормального напряжения \(\sigma\) в сечении будет также зависеть от координаты \(y.\) Ее можно оценить по закону Гука: \[\sigma = \varepsilon E = \frac{E}{R}y,\] где \(E\) − модуль упругости балки.

Изгибающий момент \(M\left( x \right)\) для заданного сечения балки относительно оси \(Oz\) вычисляется по формуле \[ {M\left( x \right) = {M_z} = \int\limits_A {\sigma ydA} } = {\frac{E}{R}\int\limits_A {{y^2}dA} } = {\frac{E}{R}I,} \] где \(I\) − момент инерции поперечного сечения относительно нейтральной оси \(Oz\) (рисунок \(2\)). Отсюда получаем выражение для радиуса кривизны балки: \[R = \frac{{EI}}{{M\left( x \right)}}.\] Известно, что радиус кривизны определяется формулой \[R = \frac{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{y''}}.\] Считая прогиб балки достаточно малым, можно пренебречь первой производной \(y'.\) Тогда дифференциальное уравнение упругой линии записывается в следующем виде: \[y'' = \frac{{M\left( x \right)}}{{EI}}\;\;\text{или}\;\;\frac{{{d^2}y}}{{d{x^2}}} = \frac{{M\left( x \right)}}{{EI}}.\] Изгибающий момент \({M\left( x \right)}\) можно выразить через известную внешнюю нагрузку \({q\left( x \right)},\) действующую на балку. Действительно, выделим малый элемент \(dx\) и рассмотрим условия его равновесия (рисунок \(3\)). Сумма проекций всех сил на ось \(Oz\) равна нулю: \[ - Q - qdx + Q + dQ = 0.\] Сумма моментов всех сил относительно, например, правой границы элемента \(dx\) (точка \(B\) на рисунке \(3\)) будет также равна нулю: \[ - M + M + dM - Qdx - q\frac{{{{\left( {dx} \right)}^2}}}{2} = 0.\] Отсюда следует соотношение \[\left\{ \begin{array}{l} \frac{{dQ}}{{dx}} = q\\ \frac{{dM}}{{dx}} = Q \end{array} \right.\;\;\text{или}\;\;\frac{{{d^2}M}}{{d{x^2}}} = q.\] С учетом этого выражения дифференциальное уравнение принимает вид: \[ {M\left( x \right) = EI\frac{{{d^2}y}}{{d{x^2}}},}\;\; {\Rightarrow \frac{{{d^2}M}}{{d{x^2}}} = \frac{{{d^2}}}{{d{x^2}}}\left( {EI\frac{{{d^2}y}}{{d{x^2}}}} \right) = q.} \] Данное уравнение называется дифференциальным уравнением Эйлера-Бернулли. В случае, если величины \(E\) и \(I\) постоянны вдоль оси \(Ox,\) мы получаем уравнение четвертого порядка: \[EI\frac{{{d^4}y}}{{d{x^4}}} = q.\] Данное уравнение при задании соответствующих граничных условий определяет прогиб нагруженной балки.

   Пример 1

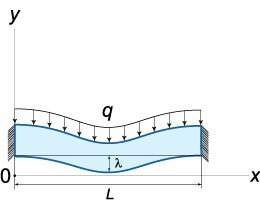
Определить прогиб балки, жестко закрепленной с обоих концов и нагруженной равномерно распределенной силой (рисунок \(4\)).
Пусть на балку длиной \(L\) действует однородно распределенная сила \(q.\) Модуль упругости \(E\) и момент инерции балки \(I\) считаем известными.

Уравнение прогиба балки имеет вид: \[EI\frac{{{d^4}y}}{{d{x^4}}} = - q.\] Знак "минус" перед \(q\) показывает, что сила направлена в сторону, противоположную положительному направлению оси \(Oy,\) т.е. вертикально вниз.

При жестком закреплении концов балки справедливы следующие граничные условия: \[ {y\left( {x = 0} \right) = 0,}\;\; {y\left( {x = L} \right) = 0,}\;\; {\frac{{dy}}{{dx}}\left( {x = 0} \right) = 0,}\;\; {\frac{{dy}}{{dx}}\left( {x = L} \right) = 0.} \] Последовательно интегрируя дифференциальное уравнение, находим функцию \(y\left( x \right):\) \[ {\frac{{{d^3}y}}{{d{x^3}}} = - \frac{{qx}}{{EI}} + {C_1},}\;\; {\Rightarrow \frac{{{d^2}y}}{{d{x^2}}} = - \frac{{q{x^2}}}{{2EI}} + {C_1}x + {C_2},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = - \frac{{q{x^3}}}{{6EI}} + \frac{{{C_1}{x^2}}}{2} + {C_2}x + {C_3},}\;\; {\Rightarrow y\left( x \right) = - \frac{{q{x^4}}}{{24EI}} + \frac{{{C_1}{x^3}}}{6} + \frac{{{C_2}{x^2}}}{2} + {C_3}x + {C_4}.} \] Из условий \(y\left( {x = 0} \right) = 0\) и \(\large\frac{{dy}}{{dx}}\normalsize\left( {x = 0} \right) = 0\) следует, что \({C_3} = {C_4} = 0.\) С учетом двух других граничных условий получаем следующую систему уравнений с неизвестными \({C_1}\) и \({C_2}:\) \[\left\{ \begin{array}{l} - \frac{{q{L^4}}}{{24EI}} + \frac{{{C_1}{L^3}}}{6} + \frac{{{C_2}{L^2}}}{2} = 0\\ - \frac{{q{L^3}}}{{6EI}} + \frac{{{C_1}{L^2}}}{2} + {C_2}L = 0 \end{array} \right..\] Решая ее, находим коэффициенты \({C_1}\) и \({C_2}:\) \[ {\left\{ \begin{array}{l} \left. { - \frac{{q{L^4}}}{{24EI}} + \frac{{{C_1}{L^3}}}{6} + \frac{{{C_2}{L^2}}}{2} = 0\;} \right| \cdot \frac{{24}}{{{L^2}}}\\ \left. { - \frac{{q{L^3}}}{{6EI}} + \frac{{{C_1}{L^2}}}{2} + {C_2}L = 0\;} \right| \cdot \frac{6}{L} \end{array} \right.,}\;\; {\Rightarrow \left. {\left\{ {\begin{array}{*{20}{l}} { - \frac{{q{L^2}}}{{EI}} + 4{C_1}L + 12{C_2} = 0}\\ { - \frac{{2q{L^2}}}{{EI}} + 6{C_1}L + 12{C_2} = 0} \end{array}\;} \right.} \right| - ,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{C_1} = \frac{{qL}}{{2EI}}}\\ {{C_2} = - \frac{{q{L^2}}}{{12EI}}} \end{array}} \right..} \] Итак, прогиб балки под действием равномерно распределенной нагрузки \(q\) описывается функцией \[ {y\left( x \right) = - \frac{{q{x^4}}}{{24EI}} + \frac{{qL{x^3}}}{{12EI}} - \frac{{q{L^2}{x^2}}}{{24EI}} } = { - \frac{{q{x^2}}}{{24EI}}\left( {{x^2} - 2Lx + {L^2}} \right) } = { - \frac{{q{x^2}}}{{24EI}}{\left( {x - L} \right)^2}.} \] Чтобы определить стрелу прогиба \(\lambda,\) исследуем функцию \(f\left( x \right) = {x^2}{\left( {x - L} \right)^2}\) на экстремум. Находим производную этой функции и приравниваем ее нулю: \[ {f'\left( x \right) = {\left[ {{x^2}{{\left( {x - L} \right)}^2}} \right]^\prime } } = {2x{\left( {x - L} \right)^2} + 2{x^2}\left( {x - L} \right) } = {2x\left( {x - L} \right)\left( {x - L + x} \right) } = {2x\left( {x - L} \right)\left( {2x - L} \right) = 0.} \] Отсюда следует, что данная функция имеет экстремум при \(x = \large\frac{L}{2}\normalsize.\) В этой точке функция \(f\left( x \right)\) принимает максимальное значение, равное \[f\left( {\frac{L}{2}} \right) = {\left( {\frac{L}{2}} \right)^2}{\left( { - \frac{L}{2}} \right)^2} = \frac{{{L^4}}}{{16}}.\] Тогда стрела прогиба \(\lambda\) будет определяться формулой \[\lambda = \frac{q}{{24EI}} \cdot \frac{{{L^4}}}{{16}} = \frac{{q{L^4}}}{{384EI}}.\] Оказывается, что величина прогиба \(\lambda\) пропорциональна длине балки в четвертой степени! Такая крайне сильная зависимость накладывает существенные ограничения на конструкцию зданий и сооружений.

   Пример 2

Тонкий цилиндрический вал длиной \(L\) вращается с угловой скоростью \(\omega.\) При какой скорости \(\omega\) может произойти разрушение вала? Модуль упругости материала \(E,\) масса вала \(M,\) радиус сечения \(a.\)

При вращении вала на него действует центробежная сила, которая пропорциональна отклонению \(y\) от оси вращения. При увеличении в некоторой точке деформации \(y\) центробежная сила в этой точке также будет возрастать, что приведет к дальнейшему искривлению вала. Неустойчивость такого рода возникает при определенных частотах и может привести к разрушению вала.

Исследуем эту задачу с помощью дифференциального уравнения. Базовое уравнение, описывающее деформацию вала, записывается в виде: \[EI\frac{{{d^4}y}}{{d{x^4}}} = f,\] где \(f\) обозначает плотность центробежной силы.

На элемент вала \(dx\) действует центробежная сила, равная \[dF = {\omega ^2}y\frac{M}{L}dx.\] Здесь величина \({\large\frac{M}{L}\normalsize} dx\) соответствует массе элемента \(dx,\) \(y\) − прогиб вала, равный радиусу вращения элемента \(dx.\) В результате наше дифференциальное уравнение принимает вид: \[ {EI\frac{{{d^4}y}}{{d{x^4}}} = \frac{{{\omega ^2}M}}{L}y}\;\;\; {\text{или}\;\;\;\frac{{{d^4}y}}{{d{x^4}}} - {\alpha ^4}y = 0,} \] где введено обозначение \({\alpha ^4} = \large\frac{{{\omega ^2}M}}{{EIL}}\normalsize.\)

Итак, мы получили красивое линейное дифференциальное уравнение четвертого порядка. Найдем корни характеристического уравнения. \[ {{s^4} - {\alpha ^4} = 0,}\;\; {\Rightarrow \left( {{s^2} - {\alpha ^2}} \right)\left( {{s^2} + {\alpha ^2}} \right) = 0,}\;\; {\Rightarrow \left( {s - \alpha } \right)\left( {s + \alpha } \right)\left( {{s^2} + {\alpha ^2}} \right) = 0.} \] Корни имеют такие значения: \[ {{s_1} = \alpha ,\;\;{s_2} = - \alpha ,}\;\; {{s_3} = \alpha i,\;\;{s_4} = - \alpha i.} \] Тогда общее решение уравнения выражается формулой \[ {y\left( x \right) = {C_1}{e^{\alpha x}} + {C_2}{e^{ - \alpha x}} } + {{C_3}\cos \alpha x + {C_4}\sin\alpha x.} \] Коэффициенты \({C_i}\) находятся из граничных условий. В данном случае, учитывая, что вал вращается на двух опорах, граничные условия имеют вид:

• прогиб вала в точках \(x = 0\) и \(x = L\) равен нулю;

• кривизна вала в точках \(x = 0\) и \(x = L\) равна нулю.

Следовательно, \[ {y\left( {x = 0} \right) = 0,\;\;y\left( {x = L} \right) = 0,}\;\; {\frac{{{d^2}y}}{{d{x^2}}}\left( {x = 0} \right) = 0,}\;\; {\frac{{{d^2}y}}{{d{x^2}}}\left( {x = L} \right) = 0.} \] Находим вторую производную функции \(y\left( x \right):\) \[ {\frac{{dy}}{{dx}} = {C_1}\alpha {e^{\alpha x}} - {C_2}\alpha {e^{ - \alpha x}} } - {{C_3}\alpha \sin \alpha x } + {{C_4}\alpha \cos\alpha x,} \] \[ {\frac{{{d^2}y}}{{d{x^2}}} = {C_1}{\alpha ^2}{e^{\alpha x}} + {C_2}{\alpha ^2}{e^{ - \alpha x}} } - {{C_3}{\alpha ^2}\cos\alpha x } - {{C_4}{\alpha ^2}\sin\alpha x.} \] Подставляя \(y\) и \(\large\frac{{{d^2}y}}{{d{x^2}}}\normalsize\) в граничные условия, получаем \[ \left\{ \begin{array}{l} {C_1} + {C_2} + {C_3} = 0\\ {C_1} + {C_2} - {C_3} = 0\\ {C_1}{e^{\alpha L}} + {C_2}{e^{ - \alpha L}} + {C_3}\cos\alpha L + {C_4}\sin\alpha L = 0\\ {C_1}{e^{\alpha L}} + {C_2}{e^{ - \alpha L}} - {C_3}\cos\alpha L - {C_4}\sin\alpha L = 0 \end{array} \right.. \] Решение этой системы имеет вид: \[\left\{ \begin{array}{l} {C_1} = 0\\ {C_2} = 0\\ {C_3} = 0\\ {C_4}\sin\alpha L = 0 \end{array} \right..\] Случаю \({C_4} = 0\) соответствует тривиальное решение \(y = 0.\) В этом случае вал остается недеформированным. Содержательное решение существует при \({C_4} \ne 0.\) Тогда должно выполняться условие \[\sin \alpha L = 0,\;\; \Rightarrow \alpha L = \pi n,\;\;n = 1,2,3, \ldots \] Заметим, что число \(n\) здесь больше нуля, поскольку при \(n = 0\) мы снова получаем тривиальное решение \(y = 0.\)

Итак, при \(\alpha L = \pi n\) вал вращения начинает искривляться, принимая форму синусоиды: \[y\left( x \right) = {C_4}\sin \alpha x = {C_4}\sin \left( {\frac{{\pi n}}{L}x} \right).\] Минимальная критическая частота \({\omega _\text{кр}},\) при которой возникает данная неустойчивость, находится по следующей формуле: \[ {\alpha = \frac{\pi }{L}\left( {\text{при}\;n = 1} \right),}\;\; {\Rightarrow \frac{{\omega _\text{кр}^2M}}{{EIL}} = {\alpha ^4} = {\left( {\frac{\pi }{L}} \right)^4},}\;\; {\Rightarrow \omega _\text{кр}^2 = \frac{{{\pi ^4}}}{{{L^4}}}\frac{{EIL}}{M} = \frac{{{\pi ^4}}}{{{L^3}}}\frac{{EI}}{M},}\;\; {\Rightarrow {\omega _\text{кр}} = \frac{{{\pi ^2}}}{L}\sqrt {\frac{{EI}}{{LM}}} .} \] Если вал представляет собой цельный стержень с радиусом поперечного сечения \(a,\) то его момент инерции относительно центральной оси равен \[I = \frac{{M{a^2}}}{{4L}}.\] Подставляя \(I\) в предыдущую формулу, находим минимальную критическую скорость вращения вала: \[ {{\omega _\text{кр}} = \frac{{{\pi ^2}}}{L}\sqrt {\frac{{EI}}{{LM}}} } = {\frac{{{\pi ^2}}}{L}\sqrt {\frac{E}{{LM}} \cdot \frac{{M{a^2}}}{{4L}}} } = {\frac{{{\pi ^2}a}}{{2{L^2}}}\sqrt E .} \]