Поверхностные интегралы первого рода

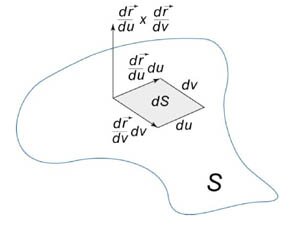
Рассмотрим скалярную функцию \(f\left( {x,y,z} \right)\) и поверхность \(S.\) Пусть \(S\) задана векторной функцией \[\mathbf{r}\left( {u,v} \right) = x\left( {u,v} \right)\mathbf{i} + y\left( {u,v} \right)\mathbf{j} + z\left( {u,v} \right)\mathbf{k},\] где координаты \(\left( {u,v} \right)\) изменяются в пределах некоторой области определения \(D\left( {u,v} \right)\) в плоскости \(uv.\) Заметим, что функция \(f\left( {x,y,z} \right)\) рассматривается только в точках, принадлежащих поверхности \(S,\) то есть \[f\left[ {\mathbf{r}\left( {u,v} \right)} \right] = f\left[ {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right].\] Поверхностный интеграл первого рода от функции \(f\left( {x,y,z} \right)\) по поверхности \(S\) определяется следующим образом: \[ {\iint\limits_S {f\left( {x,y,z} \right)dS} } = {\iint\limits_{D\left( {u,v} \right)} {f\left( {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right)\left| {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right|dudv} ,} \] где частные производные \({\large\frac{{\partial \mathbf{r}}}{{\partial u}}\normalsize}\) и \({\large\frac{{\partial \mathbf{r}}}{{\partial v}}\normalsize}\) равны \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} } = {\frac{{\partial x}}{{\partial u}}\left( {u,v} \right)\mathbf{i} + \frac{{\partial y}}{{\partial u}}\left( {u,v} \right)\mathbf{j} + \frac{{\partial z}}{{\partial u}}\left( {u,v} \right)\mathbf{k},} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial v}} } = {\frac{{\partial x}}{{\partial v}}\left( {u,v} \right)\mathbf{i} + \frac{{\partial y}}{{\partial v}}\left( {u,v} \right)\mathbf{j} + \frac{{\partial z}}{{\partial v}}\left( {u,v} \right)\mathbf{k},} \] а \({\large\frac{{\partial \mathbf{r}}}{{\partial u}}\normalsize \times \large\frac{{\partial \mathbf{r}}}{{\partial v}}\normalsize}\) означает векторное произведение. Вектор \({\large\frac{{\partial \mathbf{r}}}{{\partial u}}\normalsize \times \large\frac{{\partial \mathbf{r}}}{{\partial v}}\normalsize}\) перпендикулярен поверхности в точке \({\mathbf{r}\left( {u,v} \right)}.\)

Абсолютное значение \(dS = \left| {\large\frac{{\partial \mathbf{r}}}{{\partial u}}\normalsize \times \large\frac{{\partial \mathbf{r}}}{{\partial v}}\normalsize} \right|dudv\) называется элементом площади: оно соответствует изменению площади \(dS\) в результате приращения координат \(u\) и \(v\) на малые значения \(du\) и \(dv\) (рисунок \(1\)). Площадь поверхности \(S\) выражается с помощью поверхностного интеграла в виде \[A = \iint\limits_S {dS} .\] Если поверхность \(S\) задана уравнением \(z = z\left( {x,y} \right),\) где \(z\left( {x,y} \right)\) − дифференцируемая функция в области \(D\left( {x,y} \right),\) то поверхностный интеграл находится по формуле \[ {\iint\limits_S {f\left( {x,y,z} \right)dS} } = {\iint\limits_{D\left( {x,y} \right)} {f\left( {x,y,z\left( {x,y} \right)} \right)\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} .} \] Если поверхность \(S\) состоит из нескольких частей \({S_i},\) то для вычисления поверхностного интеграла можно использовать свойство аддитивности: \[ {\iint\limits_S {f\left( {x,y,z} \right)dS} } = {\sum\limits_{i = 1}^n {\iint\limits_{{S_i}} {f\left( {x,y,z} \right)d{S_i}} } .} \]

   Пример 1

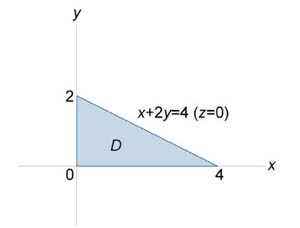
Вычислить поверхностный интеграл \(\iint\limits_S {\left( {x + y + z} \right)dS},\) где \(S\) − часть плоскости \(x + 2y + 4z = 4,\) лежащая в первом октанте \(\left( {x \ge 0,\;y \ge 0,z \ge 0} \right).\) Запишем уравнение плоскости в виде \[z = z\left( {x,y} \right) = 1 - \frac{x}{4} - \frac{y}{2}.\] Найдем частные производные \[\frac{{\partial z}}{{\partial x}} = - \frac{1}{4},\;\;\frac{{\partial z}}{{\partial y}} = - \frac{1}{2}.\] Применяя формулу \[ {\iint\limits_S {f\left( {x,y,z} \right)dS} } = {\iint\limits_{D} {f\left( {x,y,z\left( {x,y} \right)} \right)\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy},} \] поверхностный интеграл можно выразить через двойной интеграл: \[ {I = \iint\limits_S {\left( {x + y + z} \right)dS} } = {\iint\limits_D {\left( {x + y + 1 - \frac{x}{4} - \frac{y}{2}} \right)\sqrt {1 + {{\left( { - \frac{1}{4}} \right)}^2} + {{\left( { - \frac{1}{2}} \right)}^2}} dxdy} } = {\iint\limits_D {\left( {\frac{{3x}}{4} + \frac{y}{2} + 1} \right)\frac{{\sqrt {21} }}{4}dxdy} .} \] Область интегрирования \(D\) представляет собой треугольник, показанный выше на рисунке \(2.\) Вычисляем окончательно заданный интеграл: \[ {I = \frac{{\sqrt {21} }}{4}\int\limits_0^2 {\left[ {\int\limits_0^{4 - 2y} {\left( {\frac{{3x}}{4} + \frac{y}{2} + 1} \right)dx} } \right]dy} } = {\frac{{\sqrt {21} }}{{16}}\int\limits_0^2 {\left[ {\int\limits_0^{4 - 2y} {\left( {3x + 2y + 4} \right)dx} } \right]dy} } = {\frac{{\sqrt {21} }}{{16}}\int\limits_0^2 {\left[ {\left. {\left( {\frac{{3{x^2}}}{2} + 2yx + 4x} \right)} \right|_{x = 0}^{4 - 2y}} \right]dy} } = {\frac{{\sqrt {21} }}{{16}}\int\limits_0^2 {\left[ {\frac{3}{2}{{\left( {4 - 2y} \right)}^2} + 2\left( {4 - 2y} \right)y + 4\left( {4 - 2y} \right)} \right]dy} } = {\frac{{\sqrt {21} }}{{32}}\int\limits_0^2 {\left[ {3{{\left( {16 - 16y + 4{y^2}} \right)}^2} + 16y - 8{y^2} + 32 - 16y} \right]dy} } = {\frac{{\sqrt {21} }}{{32}}\int\limits_0^2 {\left( {80 - 48y + 4{y^2}} \right)dy} } = {\frac{{\sqrt {21} }}{4}\int\limits_0^2 {\left( {20 - 12y + {y^2}} \right)dy} } = {\frac{{\sqrt {21} }}{4}\left[ {\left. {\left( {20y - 6{y^2} + \frac{{{y^3}}}{3}} \right)} \right|_0^2} \right] } = {\frac{{\sqrt {21} }}{4}\left( {40 - 24 + \frac{8}{3}} \right) } = {\frac{{7\sqrt {21} }}{3}.} \]

   Пример 2

Вычислить интеграл \(\iint\limits_S {{z^2}dS},\) где \(S\) представляет собой полную поверхность конуса \(\sqrt {{x^2} + {y^2}} \le z \le 2.\) Обозначим через \({S_1}\) боковую поверхность конуса, и через \({S_2}\) − его основание. Запишем данный интеграл в виде суммы двух интегралов \[ {I = {I_1} + {I_2} } = {\iint\limits_{{S_1}} {{z^2}d{S_1}} + \iint\limits_{{S_2}} {{z^2}d{S_2}} .} \] Найдем сначала первый интеграл \({I_1},\) используя формулу \[ {{I_1} = \iint\limits_{{S_1}} {{z^2}d{S_1}} } = {\iint\limits_D {f\left( {x,y,z\left( {x,y} \right)} \right)\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} .} \] Частные производные здесь равны \[\frac{{\partial z}}{{\partial x}} = \frac{\partial }{{\partial x}}\sqrt {{x^2} + {y^2}} = \frac{x}{{\sqrt {{x^2} + {y^2}} }},\] \[\frac{{\partial z}}{{\partial y}} = \frac{\partial }{{\partial y}}\sqrt {{x^2} + {y^2}} = \frac{y}{{\sqrt {{x^2} + {y^2}} }}.\] Тогда \[ {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} } = {\sqrt {1 + {{\left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2} + {{\left( {\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2}} } = {\sqrt {1 + \frac{{{x^2}}}{{{x^2} + {y^2}}} + \frac{{{y^2}}}{{{x^2} + {y^2}}}} } = {\sqrt 2 .} \] Поскольку \(z = 2\) для основания конуса, то область интегрирования \(D\left( {x,y} \right)\) определяется неравенством \({z^2} + {y^2} \le 4\) (рисунок \(3\)). Следовательно, интеграл \({I_1}\) записывается в виде \[ {{I_1} = \iint\limits_{{S_1}} {{z^2}d{S_1}} } = {\sqrt 2 \iint\limits_{D\left( {x,y} \right)} {\left( {{x^2} + {y^2}} \right)dxdy} .} \] Его легко вычислить в полярных координатах: \[ {{I_1} = \sqrt 2 \iint\limits_{D\left( {x,y} \right)} {\left( {{x^2} + {y^2}} \right)dxdy} } = {\sqrt 2 \int\limits_0^{2\pi } {\int\limits_0^2 {{r^2} \cdot rdrd\varphi } } } = {\sqrt 2 \int\limits_0^{2\pi } d \varphi \int\limits_0^2 {{r^3}dr} } = {\sqrt 2 \cdot 2\pi \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^2} \right] } = {\frac{{\sqrt 2 \pi }}{2}\left( {{2^4} - 0} \right) } = {8\sqrt 2 \pi .} \] Рассмотрим теперь второй интеграл \({I_2}.\) Уравнение основания конуса имеет вид \(z = 2.\) Поэтому, \[{I_2} = \iint\limits_{{S_2}} {{2^2}d{S_2}} = 4\iint\limits_{{S_2}} {d{S_2}} ,\] где \(\iint\limits_{{S_2}} {d{S_2}} \) равно площади основания \(\pi \cdot {2^2} = 4\pi .\) Тогда \[ {{I_2} = 4\iint\limits_{{S_2}} {d{S_2}} } = {4 \cdot 4\pi = 16\pi .} \] Таким образом, полное значение поверхностного интеграла равно \[ {I = {I_1} + {I_2} } = {8\sqrt 2 \pi + 16\pi } = {8\pi \left( {\sqrt 2 + 2} \right).} \]

   Пример 3

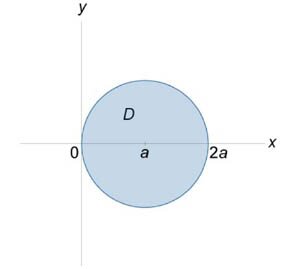
Вычислить интеграл \(\iint\limits_S {\left( {xy + yz + zx} \right)dS},\) где \(S\) − часть конуса \(z = \sqrt {{x^2} + {y^2}} \) внутри поверхности \({x^2} + {y^2} = 2ax.\) Определим сначала область интегрирования \(D,\) которая является проекцией поверхности \(S\) на плоскость \(Oxy.\) Запишем уравнение \({x^2} + {y^2} = 2ax\) в следующем виде: \[ {{x^2} - 2ax + {y^2} = 0,}\;\; {\Rightarrow {x^2} - 2ax + {a^2} + {y^2} = {a^2},}\;\; {\Rightarrow {\left( {x - a} \right)^2} + {y^2} = {a^2}.} \] Как видно, область интегрирования \(D\) представляет собой круг с центром в точке \(\left( {a,0} \right)\) (рисунок \(4\)). Поскольку частные производные равны \[\frac{{\partial z}}{{\partial x}} = \frac{\partial }{{\partial x}}\sqrt {{x^2} + {y^2}} = \frac{x}{{\sqrt {{x^2} + {y^2}} }},\] \[\frac{{\partial z}}{{\partial y}} = \frac{\partial }{{\partial y}}\sqrt {{x^2} + {y^2}} = \frac{y}{{\sqrt {{x^2} + {y^2}} }},\] то элемент площади конической поверхности имеет вид \[ {dS = \sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy } = {\sqrt {1 + {{\left( {\frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2} + {{\left( {\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right)}^2}} dxdy } = {\sqrt 2 dxdy.} \] Следовательно, по формуле \[ {\iint\limits_S {f\left( {x,y,z} \right)dS} } = {\iint\limits_D {f\left( {x,y,z\left( {x,y} \right)} \right)\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} } \] получаем \[ {I = \iint\limits_S {\left( {xy + yz + zx} \right)dS} } = {\sqrt 2 \iint\limits_{D\left( {x,y} \right)} {\left( {xy + \left( {y + x} \right)\sqrt {{x^2} + {y^2}} } \right)dxdy} .} \] Для вычисления полученного интеграла удобно перейти к полярным координатам. Область интегрирования \(D\) при этом принимает вид \[D = \left\{ {\left( {r,\varphi } \right)|\;0 \le r \le 2a\cos \varphi , - \frac{\pi }{2} \le \varphi \le \frac{\pi }{2}} \right\}.\] Тогда интеграл равен \[ {I = \sqrt 2 \iint\limits_{D\left( {r,\varphi } \right)} {\left[ {r\cos \varphi \cdot r\sin \varphi + \left( {r\sin \varphi + r\cos \varphi } \right)\sqrt {{r^2}} } \right]rdrd\varphi } } = {\sqrt 2 \int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {\cos \varphi \sin \varphi + \sin \varphi + \cos \varphi } \right)d\varphi } \int\limits_0^{2a\cos \varphi } {{r^3}dr} } = {\sqrt 2 \int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left[ {\left( {\cos \varphi \sin \varphi + \sin \varphi + \cos \varphi } \right) \cdot \left( {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^{2a\cos \varphi }} \right)} \right]d\varphi } } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {\cos \varphi \sin \varphi + \sin \varphi + \cos \varphi } \right){{\cos }^4}\varphi d\varphi } } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left[ {\left( {{{\cos }^5}\varphi + {{\cos }^4}\varphi } \right)\sin\varphi + {{\cos }^5}\varphi } \right]d\varphi } } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {{{\cos }^5}\varphi + {{\cos }^4}\varphi } \right)\sin\varphi d\varphi } } + {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{\cos^5}\varphi d\varphi } } = {{I_1} + {I_2}.} \] В последней формуле интеграл \({I_1}\) равен нулю, поскольку подынтегральная функция является нечетной, а интегрирование выполняется в интервале, симметричном относительно начала координат. Отсюда следует, что \[ {I = {I_2} = 4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{\cos^5}\varphi d\varphi } } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{\cos^4}\varphi \cos \varphi d\varphi } } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{{\left( {{\cos^2}\varphi } \right)}^2}d\left( {\sin \varphi } \right)} } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{{\left( {1 - {\sin^2}\varphi } \right)}^2}d\left( {\sin \varphi } \right)} } = {4\sqrt 2 {a^4}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {1 - 2{\sin^2}\varphi + {{\sin }^4}\varphi } \right)d\left( {\sin \varphi } \right)} } = {4\sqrt 2 {a^4}\left[ {\left. {\left( {\sin \varphi - \frac{{2{{\sin }^3}\varphi }}{3} + \frac{{{{\sin }^5}\varphi }}{5}} \right)} \right|_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize}} \right] } = {8\sqrt 2 {a^4}\left[ {\sin \frac{\pi }{2} - \frac{2}{3}{{\sin }^3}\left( {\frac{\pi }{2}} \right) + \frac{1}{5}{{\sin }^5}\left( {\frac{\pi }{2}} \right)} \right] } = {8\sqrt 2 {a^4}\left( {1 - \frac{2}{3} + \frac{1}{5}} \right) } = {\frac{{64\sqrt 2 {a^4}}}{{15}}.} \]

   Пример 4

Найти интеграл \(\iint\limits_S {xdS},\) где поверхность \(S\) − часть сферы \({x^2} + {y^2} + {z^2} = {a^2},\) лежащая в первом октанте. Данный интеграл удобно вычислять в сферических координатах. Элемент площади в сферических координатах имеет вид \(dS = {a^2}\sin \theta d\psi d\theta .\) Поскольку \(x = a\cos \psi \sin \theta ,\) то интеграл можно записать в следующей форме: \[ {I = \iint\limits_S {xdS} } = {\iint\limits_{D\left( {\psi ,\theta } \right)} {a\cos \psi \sin \theta \cdot {a^2}\sin \theta d\psi d\theta } } = {{a^3}\iint\limits_{D\left( {\psi ,\theta } \right)} {\cos \psi \,{{\sin }^2}\theta d\psi d\theta } .} \] Область интегрирования \(D\left( {\psi ,\theta } \right)\) определяется как \[D = \left\{ {\left( {\psi ,\theta } \right)|\;0 \le \psi \le \frac{\pi }{2},0 \le \theta \le \frac{\pi }{2}} \right\}.\] Следовательно, интеграл равен \[ {I = {a^3}\iint\limits_{D\left( {\psi ,\theta } \right)} {\cos \psi \,{{\sin }^2}\theta d\psi d\theta } } = {{a^3}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos \psi d\psi } \int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\sin }^2}\theta d\theta } } = {{a^3} \cdot \left[ {\left. {\left( {\sin \psi } \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] \cdot \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{1 - \cos 2\theta }}{2}d\theta } } = {{a^3} \cdot 1 \cdot \frac{1}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 - \cos 2\theta } \right)d\theta } } = {\frac{{{a^3}}}{2}\left[ {\left. {\left( {\theta - \frac{{\sin 2\theta }}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{{{a^3}}}{2} \cdot \frac{\pi }{2} } = {\frac{{\pi {a^3}}}{4}.} \]

   Пример 5

Найти интеграл \(\iint\limits_S {\large\frac{{dS}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}\normalsize} ,\) где \(S\) − часть цилиндрической поверхности, заданной параметрически в виде \(\mathbf{r}\left( {u,v} \right) = \left( {a\cos u,a\sin u,v} \right),\) \(0 \le u \le 2\pi ,\) \(0 \le v \le H.\) Вычислим частные производные: \[\frac{{\partial \mathbf{r}}}{{\partial u}} = \left( {\frac{{\partial x}}{{\partial u}},\frac{{\partial y}}{{\partial u}},\frac{{\partial z}}{{\partial u}}} \right) = \left( { - a\sin u,a\cos u,0} \right),\] \[\frac{{\partial \mathbf{r}}}{{\partial v}} = \left( {\frac{{\partial x}}{{\partial v}},\frac{{\partial y}}{{\partial v}},\frac{{\partial z}}{{\partial v}}} \right) = \left( {0,0,1} \right)\] и их векторное произведение: \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ { - a\sin u} & {a\cos u} & 0\\ 0 & 0 & 1 \end{array}} \right| } = {a\cos u \cdot \mathbf{i} + a\sin u \cdot \mathbf{j} + 0 \cdot \mathbf{k}.} \] Тогда, элемент площади заданной поверхности равен \[ {dS = \left| {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right|dudv } = {\left| {\sqrt {{{\left( {a\cos u} \right)}^2} + {{\left( {a\sin u} \right)}^2}} } \right|dudv } = {adudv.} \] Теперь можно вычислить поверхностный интеграл: \[ {\iint\limits_S {\frac{{dS}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}} } = {\iint\limits_{D\left( {u,v} \right)} {\frac{{adudv}}{{\sqrt {{{\left( {a\cos u} \right)}^2} + {{\left( {a\sin u} \right)}^2} + {v^2}} }}} } = {\iint\limits_{D\left( {u,v} \right)} {\frac{{adudv}}{{\sqrt {{a^2} + {v^2}} }}} } = {\int\limits_0^{2\pi } {adu} \int\limits_0^H {\frac{{dv}}{{\sqrt {{a^2} + {v^2}} }}} } = {2\pi a\int\limits_0^H {\frac{{dv}}{{\sqrt {{a^2} + {v^2}} }}} } = {2\pi a\left[ {\left. {\ln \left( {v + \sqrt {{a^2} + {v^2}} } \right)} \right|_{v = 0}^H} \right] } = {2\pi a\left[ {\ln \left( {H + \sqrt {{a^2} + {H^2}} } \right) - \ln a} \right] } = {2\pi a\ln \frac{{H + \sqrt {{a^2} + {H^2}} }}{a}.} \]

   Пример 6

Вычислить интеграл \(\iint\limits_S {\sqrt {1 + {x^2} + {y^2}} dS} .\) Поверхность \(S\) задана параметрически в виде \(\mathbf{r}\left( {u,v} \right) = u\cos v \cdot \mathbf{i} + u\sin v \cdot \mathbf{j} + v \cdot \mathbf{k},\) \(0 \le u \le 2,\) \(0 \le v \le \pi .\) Найдем частные производные и их векторное произведение: \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} } = {\frac{\partial }{{\partial u}}\left( {u\cos v,u\sin v,v} \right) } = {\left( {\cos v,\sin v,0} \right),} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial v}} } = {\frac{\partial }{{\partial v}}\left( {u\cos v,u\sin v,v} \right) } = {\left( { - u\sin v,u\cos v,1} \right),} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ {\cos v} & {\sin v} & 0\\ { - u\sin v} & {u\cos v} & 1 \end{array}} \right| } = {\sin v \cdot \mathbf{i} - \cos v \cdot \mathbf{j} + \left( {u\,{{\cos }^2}v + u\,{{\sin }^2}v} \right) \cdot \mathbf{k} } = {\sin v \cdot \mathbf{i} - \cos v \cdot \mathbf{j} + u \cdot \mathbf{k}.} \] Тогда элемент площади равен \[ {dS = \left| {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right|dudv } = {\sqrt {1 + {{\left( {u\cos v} \right)}^2} + {{\left( {u\sin v} \right)}^2}} dudv } = {\sqrt {1 + {u^2}} dudv.} \] Теперь несложно вычислить заданный поверхностный интеграл: \[ {\iint\limits_S {\sqrt {1 + {x^2} + {y^2}} dS} } = {\iint\limits_{D\left( {u,v} \right)} {\sqrt {1 + {{\left( {u\cos v} \right)}^2} + {{\left( {u\sin v} \right)}^2}} \sqrt {1 + {u^2}} dudv} } = {\iint\limits_{D\left( {u,v} \right)} {\left( {1 + {u^2}} \right)dudv} } = {\int\limits_0^\pi {dv} \int\limits_0^2 {\left( {1 + {u^2}} \right)du} } = {\pi \cdot \left[ {\left. {\left( {u + \frac{{{u^3}}}{3}} \right)} \right|_0^2} \right] } = {\frac{{14\pi }}{3}.} \]