|
Отопление дома
|
||||||||||||
|
Любой хозяин подтвердит, что отопление дома − это дорогое удовольствие. Помимо расходов, это ведь еще и углеродное загрязнение окружающей среды! Оказывается, что используя систему дифференциальных уравнений, вполне возможно описать изменение температуры в доме при различных режимах отопления. Такая модель может принести реальную практическую пользу.
Рассмотрим типичный двухэтажный дом (рисунок \(1\)). Температуру внутри дома будем описывать двумя функциями:
Введем следующие коэффициенты \({k_i},\) характеризующие двухэтажный дом:
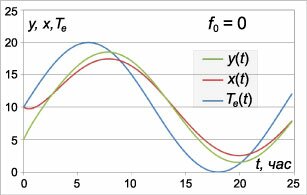
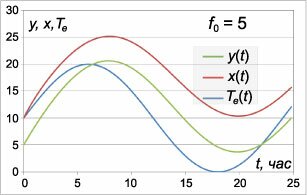
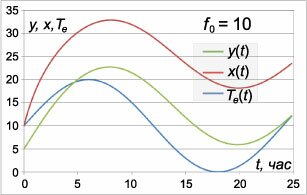
Запишем данную систему в векторно-матричной форме: \[ {\mathbf{X'}\left( t \right) = K\mathbf{X}\left( t \right) + \mathbf{F}\left( t \right),}\;\; {\text{где}\;\;\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {x\left( t \right)}\\ {y\left( t \right)} \end{array}} \right),}\;\; {K = \left( {\begin{array}{*{20}{c}} { - {k_1} - {k_2} - {k_3}}&{{k_2}}\\ {{k_2}}&{ - {k_2} - {k_4}} \end{array}} \right),}\;\; {\mathbf{F}\left( t \right) = {\mathbf{F}_1}\left( t \right) + {\mathbf{F}_2}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{k_1}{T_g} + {k_3}{T_e}\left( t \right)}\\ {{k_4}{T_e}\left( t \right)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {f\left( t \right)}\\ 0 \end{array}} \right).} \] Здесь неоднородная часть представлена в виде суммы двух векторов. Поскольку система линейная, то для ее решения можно применить принцип суперпозиции. Рассмотрим сначала однородную систему: \[\mathbf{X}'\left( t \right) = K\mathbf{X}\left( t \right).\] Определим собственные значения матрицы \(K:\) \[\require{cancel} {\det \left( {K - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - {k_1} - {k_2} - {k_3} - \lambda }&{{k_2}}\\ {{k_2}}&{ - {k_2} - {k_4} - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( { - {k_1} - {k_2} - {k_3} - \lambda } \right)\left( { - {k_2} - {k_4} - \lambda } \right) - k_2^2 = 0,}\;\; {\Rightarrow {k_1}{k_2} + \cancel{k_2^2} + {k_2}{k_3} + \color{blue}{{k_2}\lambda} } + {{k_1}{k_4} + {k_2}{k_4} + {k_3}{k_4} + \color{blue}{{k_4}\lambda} } + {\color{blue}{{k_1}\lambda} + \color{blue}{{k_2}\lambda} + \color{blue}{{k_3}\lambda} + {\lambda ^2} - \cancel{k_2^2} = 0,}\;\; {\Rightarrow {\lambda ^2} + \color{blue}{\left( {{k_1} + 2{k_2} + {k_3} + {k_4}} \right)\lambda} + {k_1}{k_2} + {k_2}{k_3} + {k_3}{k_4} + {k_1}{k_4} + {k_2}{k_4} = 0.} \] Заметим, что в полученном характеристическом уравнении, которое является квадратным, коэффициенты всегда положительны: \[ {{k_1} + 2{k_2} + {k_3} + {k_4} > 0,}\;\; {{k_1}{k_2} + {k_2}{k_3} + {k_3}{k_4} + {k_1}{k_4} + {k_2}{k_4} > 0.} \] Поэтому, согласно критерию Рауса-Гурвица решение однородной системы будет асимптотически устойчивым. В данном случае речь идет о нулевом решении, так как именно оно является положением равновесия однородной системы. Найдем дискриминант характеристического уравнения: \[ {D = {b^2} - 4ac } = {{\left( {{k_1} + 2{k_2} + {k_3} + {k_4}} \right)^2} } - {4\left( {{k_1}{k_2} + {k_2}{k_3} + {k_3}{k_4} + {k_1}{k_4} + {k_2}{k_4}} \right) } = {k_1^2 + 4k_2^2 + k_3^2 + k_4^2 + \cancel{4{k_1}{k_2}} + 2{k_1}{k_3} } + {\color{blue}{2{k_1}{k_4}} + \cancel{4{k_2}{k_3}} + \cancel{4{k_2}{k_4}} + \color{red}{2{k_3}{k_4}} - \cancel{4{k_1}{k_2}} } - {\cancel{4{k_2}{k_3}} - \color{red}{4{k_3}{k_4}} - \color{blue}{4{k_1}{k_4}} - \cancel{4{k_2}{k_4}} } = {k_1^2 + 4k_2^2 + k_3^2 + k_4^2 + 2{k_1}{k_3} - \color{blue}{2{k_1}{k_4}} - \color{red}{2{k_3}{k_4}} } = {{\left( {{k_1} + {k_3}} \right)^2} + 4k_2^2 + k_4^2 - 2{k_1}{k_4} - 2{k_3}{k_4}} = {{\left( {{k_1} + {k_3}} \right)^2} - 2{k_4}\left( {{k_1} + {k_3}} \right) + k_4^2 + 4k_2^2 } = {{\left( {{k_1} + {k_3} - {k_4}} \right)^2} + 4k_2^2 > 0.} \] Таким образом, дискриминант характеристического уравнения всегда положителен. Это означает, что мы всегда имеем точку равновесия типа "узел". Поскольку выше уже была доказана устойчивость системы, то данная точка всегда представляет собой устойчивый узел, т.е. собственные числа \({\lambda _1},{\lambda _2}\) являются различными и принимают действительные отрицательные значения. Они определяются следующим соотношением: \[{\lambda _{1,2}} = \frac{{ - \left( {{k_1} + 2{k_2} + {k_3} + {k_4}} \right) \pm \sqrt {{{\left( {{k_1} + {k_3} - {k_4}} \right)}^2} + 4k_2^2} }}{2}.\] Далее, для избежания громоздких выражений, рассмотрим задачу с конкретными значениями коэффициентов теплопроводности \({{k_i}}.\) Возьмем, к примеру, такие значения: \[{k_1} = \frac{1}{{10}},\;\;{k_2} = \frac{1}{5},\;\;{k_3} = \frac{2}{5},\;\;{k_4} = \frac{1}{2}.\] Чем больше значение \({k_i},\) тем хуже теплоизоляция и выше теплопроводность соответствующей поверхности. При таком выборе коэффициентов \({k_i}\) дискриминант \(D\) характеристического уравнения будет равен \[ {D = {\left( {{k_1} + {k_3} - {k_4}} \right)^2} + 4k_2^2 } = {{\left( {\frac{1}{{10}} + \frac{2}{5} - \frac{1}{2}} \right)^2} + 4 \cdot {\left( {\frac{1}{5}} \right)^2} = \frac{4}{{25}}.} \] Тогда собственные числа \({\lambda _{1,2}}\) имеют следующие значения: \[ {{\lambda _{1,2}} = \frac{{ - \left( {{k_1} + 2{k_2} + {k_3} + {k_4}} \right) \pm \sqrt D }}{2} } = {\frac{{ - \left( {\frac{1}{{10}} + 2 \cdot \frac{1}{5} + \frac{2}{5} + \frac{1}{2}} \right) \pm \sqrt {\frac{4}{{25}}} }}{2} } = {\frac{{ - \frac{7}{5} \pm \frac{2}{5}}}{2} = - \frac{9}{{10}},\; - \frac{1}{2}.} \] Таким образом, \({\lambda _1} = - \large\frac{9}{{10}}\normalsize,\) \({\lambda _2} = - \large\frac{1}{{2}}\normalsize.\) Теперь вычислим собственные векторы, ассоциированные с собственными значениями \({\lambda _1},{\lambda _2}.\) Пусть собственному числу \({\lambda _1} = - \large\frac{9}{{10}}\normalsize\) соответствует вектор \({\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T},\) где индекс \(^T\) обозначает операцию транспонирования. Получаем: \[ {\left( {K - {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - {k_1} - {k_2} - {k_3} - {\lambda _1}}&{{k_2}}\\ {{k_2}}&{ - {k_2} - {k_4} - {\lambda _1}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - \frac{1}{{10}} - \frac{1}{5} - \frac{2}{5} + \frac{9}{{10}}}&{\frac{1}{5}}\\ {\frac{1}{5}}&{ - \frac{1}{5} - \frac{1}{2} + \frac{9}{{10}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {\frac{1}{5}}&{\frac{1}{5}}\\ {\frac{1}{5}}&{\frac{1}{5}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \frac{1}{5}{V_{11}} + \frac{1}{5}{V_{21}} = 0,}\;\; {\Rightarrow {V_{11}} = - {V_{21}},}\;\; {\Rightarrow {\mathbf{V}_1} = \left( {\begin{array}{*{20}{r}} { - 1}\\ 1 \end{array}} \right).} \] Аналогично найдем второй собственный вектор \({\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T},\) связанный с собственным значением \({\lambda _2} = - \large\frac{1}{{2}}\normalsize :\) \[ {\left( {K - {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - {k_1} - {k_2} - {k_3} - {\lambda _2}}&{{k_2}}\\ {{k_2}}&{ - {k_2} - {k_4} - {\lambda _2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - \frac{1}{{10}} - \frac{1}{5} - \frac{2}{5} + \frac{1}{{2}}}&{\frac{1}{5}}\\ {\frac{1}{5}}&{ - \frac{1}{5} - \frac{1}{2} + \frac{1}{{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} {-\frac{1}{5}}&{\frac{1}{5}}\\ {\frac{1}{5}}&{-\frac{1}{5}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{12}}}\\ {{V_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow -\frac{1}{5}{V_{12}} + \frac{1}{5}{V_{22}} = 0,}\;\; {\Rightarrow {V_{12}} = {V_{22}},}\;\; {\Rightarrow {\mathbf{V}_2} = \left( {\begin{array}{*{20}{r}} 1\\ 1 \end{array}} \right).} \] Общее решение однородной системы при заданных коэффициентах \({k_i}\) записывается в виде: \[ {{\mathbf{X}_0}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_0}\left( t \right)}\\ {{y_0}\left( t \right)} \end{array}} \right) } = {{C_1}{e^{ - {\large\frac{9}{{10}}\normalsize} t}}\left( {\begin{array}{*{20}{c}} { - 1}\\ 1 \end{array}} \right) + {C_2}{e^{ - {\large\frac{1}{2}\normalsize} t}}\left( {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right),} \] где постоянные \({C_1},\) \({C_2}\) зависят от начальных условий. Построим теперь решение неоднородной системы. Сначала рассмотрим неоднородную часть \({\mathbf{F}_1},\) которая описывает параметры внешней среды: \[ {{\mathbf{F}_1}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{k_1}{T_g} + {k_3}{T_e}\left( t \right)}\\ {{k_4}{T_e}\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} {\frac{1}{{10}}{T_g} + \frac{2}{5}{T_e}\left( t \right)}\\ {\frac{1}{2}{T_e}\left( t \right)} \end{array}} \right) } = {\frac{1}{{10}}\left( {\begin{array}{*{20}{c}} {{T_g} + 4{T_e}\left( t \right)}\\ {5{T_e}\left( t \right)} \end{array}} \right).} \] Пусть, например, температура земли (будем измерять ее в градусах Цельсия) составляет \({T_g} = 10^\circ\text{C}.\) Предположим также, что наружная температура изменяется с суточной периодичностью по закону \[{T_e}\left( t \right) = 10 + 10\sin \left( {\frac{{2\pi }}{{24}}t} \right) = 10 + 10\sin \left( {\frac{\pi }{{12}}t} \right),\] т.е. в интервале от \(0^\circ\text{C}\) до \(20^\circ\text{C}.\) Время \(t\) и период колебаний выражаются в часах. Тогда получаем: \[ {{\mathbf{F}_1}\left( t \right) = \frac{1}{{10}}\left( {\begin{array}{*{20}{c}} {10 + 4\left( {10 + 10\sin \left( {\frac{\pi }{{12}}t} \right)} \right)}\\ {5\left( {10 + 10\sin \left( {\frac{\pi }{{12}}t} \right)} \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} {5 + 4\sin \left( {\frac{\pi }{{12}}t} \right)}\\ {5 + 5\sin \left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right).} \] Частное решение \({\mathbf{X}_1}\left( t \right)\) для такой неоднородной части будем искать в виде векторного квазимногочлена \[ {{\mathbf{X}_1}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{y_1}\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} {{D_1} + {A_1}\sin \left( {\frac{\pi }{{12}}t} \right) + {B_1}\cos\left( {\frac{\pi }{{12}}t} \right)}\\ {{D_2} + {A_2}\sin \left( {\frac{\pi }{{12}}t} \right) + {B_2}\cos\left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right).} \] Подставляем пробное решение \({\mathbf{X}_1}\left( t \right)\) в систему уравнений с неоднородной частью \({\mathbf{F}_1}\left( t \right):\) \[{\mathbf{X'}_1}\left( t \right) = K{\mathbf{X}_1}\left( t \right) + {\mathbf{F}_1}\left( t \right),\] \[ {\Rightarrow \left( {\begin{array}{*{20}{c}} {{x'_1}\left( t \right)}\\ {{y'_1}\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} { - {k_1} - {k_2} - {k_3}}&{{k_2}}\\ {{k_2}}&{ - {k_2} - {k_4}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{y_1}\left( t \right)} \end{array}} \right) } + {\left( {\begin{array}{*{20}{c}} {{k_1}{T_g} + {k_3}{T_e}\left( t \right)}\\ {{k_4}{T_e}\left( t \right)} \end{array}} \right),} \] \[ {\Rightarrow \left( {\begin{array}{*{20}{c}} {{x'_1}\left( t \right)}\\ {{y'_1}\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} { - \frac{7}{{10}}}&{\frac{2}{{10}}}\\ {\frac{2}{{10}}}&{ - \frac{7}{{10}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{y_1}\left( t \right)} \end{array}} \right) } + {\left( {\begin{array}{*{20}{c}} {5 + 4\sin \left( {\frac{\pi }{{12}}t} \right)}\\ {5 + 5\sin \left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right),} \] \[ \Rightarrow \] \[ {{A_1}\frac{\pi }{{12}}\cos \left( {\frac{\pi }{{12}}t} \right) - {B_1}\frac{\pi }{{12}}\sin\left( {\frac{\pi }{{12}}t} \right) } = { - \frac{7}{{10}}\left[ {{D_1} + {A_1}\sin\left( {\frac{\pi }{{12}}t} \right) } + {{B_1}\cos\left( {\frac{\pi }{{12}}t} \right)} \right] } + {\frac{2}{{10}}\left[ {{D_2} + {A_2}\sin\left( {\frac{\pi }{{12}}t} \right) } + {{B_2}\cos\left( {\frac{\pi }{{12}}t} \right)} \right] } + {5 + 4\sin \left( {\frac{\pi }{{12}}t} \right),} \] \[ {{A_2}\frac{\pi }{{12}}\cos \left( {\frac{\pi }{{12}}t} \right) - {B_2}\frac{\pi }{{12}}\sin\left( {\frac{\pi }{{12}}t} \right) } = { \frac{2}{{10}}\left[ {{D_1} + {A_1}\sin\left( {\frac{\pi }{{12}}t} \right) } + {{B_1}\cos\left( {\frac{\pi }{{12}}t} \right)} \right] } - {\frac{7}{{10}}\left[ {{D_2} + {A_2}\sin\left( {\frac{\pi }{{12}}t} \right) } + {{B_2}\cos\left( {\frac{\pi }{{12}}t} \right)} \right] } + {5 + 5\sin \left( {\frac{\pi }{{12}}t} \right);} \] \[ \Rightarrow \] \[ {{A_1}\frac{\pi }{{12}}\cos \left( {\frac{\pi }{{12}}t} \right) - {B_1}\frac{\pi }{{12}}\sin\left( {\frac{\pi }{{12}}t} \right) } = { - \frac{7}{{10}}{D_1} - \frac{7}{{10}}{A_1}\sin\left( {\frac{\pi }{{12}}t} \right) } - {\frac{7}{{10}}{B_1}\cos\left( {\frac{\pi }{{12}}t} \right) } + {\frac{2}{{10}}{D_2} + \frac{2}{{10}}{A_2}\sin\left( {\frac{\pi }{{12}}t} \right) } + {\frac{2}{{10}}{B_2}\cos\left( {\frac{\pi }{{12}}t} \right) } + {5 + 4\sin \left( {\frac{\pi }{{12}}t} \right),} \] \[ {{A_2}\frac{\pi }{{12}}\cos \left( {\frac{\pi }{{12}}t} \right) - {B_2}\frac{\pi }{{12}}\sin\left( {\frac{\pi }{{12}}t} \right) } = {\frac{2}{{10}}{D_1} + \frac{2}{{10}}{A_1}\sin\left( {\frac{\pi }{{12}}t} \right) } + {\frac{2}{{10}}{B_1}\cos\left( {\frac{\pi }{{12}}t} \right) } - {\frac{7}{{10}}{D_2} - \frac{7}{{10}}{A_2}\sin\left( {\frac{\pi }{{12}}t} \right) } - {\frac{7}{{10}}{B_2}\cos\left( {\frac{\pi }{{12}}t} \right) } + {5 + 5\sin \left( {\frac{\pi }{{12}}t} \right).} \] Приравнивая коэффициенты у подобных слагаемых, получаем следующую алгебраическую систему: \[\left\{ \begin{array}{l} {A_1}\frac{\pi }{{12}} = - \frac{7}{{10}}{B_1} + \frac{2}{{10}}{B_2}\\ - {B_1}\frac{\pi }{{12}} = - \frac{7}{{10}}{A_1} + \frac{2}{{10}}{A_2} + 4\\ 0 = - \frac{7}{{10}}{D_1} + \frac{2}{{10}}{D_2} + 5\\ {A_2}\frac{\pi }{{12}} = \frac{2}{{10}}{B_1} - \frac{7}{{10}}{B_2}\\ - {B_2}\frac{\pi }{{12}} = \frac{2}{{10}}{A_1} - \frac{7}{{10}}{A_2} + 5\\ 0 = \frac{2}{{10}}{D_1} - \frac{7}{{10}}{D_2} + 5 \end{array} \right..\] Решая данную систему, находим коэффициенты \({A_1},\) \({B_1},\) \({D_1},\) \({A_2},\) \({B_2},\) \({D_2}:\) \[ {{A_1} = 6.55,\;\;{B_1} = - 3.55,}\;\; {{A_2} = 7.58,\;\;{B_2} = - 3.85,}\;\; {{D_1} = {D_2} = 10.} \] Итак, частное решение \({\mathbf{X}_1}\left( t \right)\) записывается в виде: \[ {{\mathbf{X}_1}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{y_1}\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} {10 + 6.55\sin \left( {\frac{\pi }{{12}}t} \right) - 3.55\cos \left( {\frac{\pi }{{12}}t} \right)}\\ {10 + 7.58\sin \left( {\frac{\pi }{{12}}t} \right) - 3.85\cos \left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right).} \] Аналогично найдем частное решение \({\mathbf{X}_2}\left( t \right),\) соответствующее неоднородной части \({\mathbf{F}_2}\left( t \right):\) \[{\mathbf{F}_2}\left( t \right) = \left( {\begin{array}{*{20}{c}} {f\left( t \right)}\\ 0 \end{array}} \right).\] Для источника тепла \({f\left( t \right)}\) можно запрограммировать различные режимы работы. Мы ограничимся рассмотрением простого случая, когда источник тепла действует постоянно: \(f\left( t \right) = {f_0}.\) Тогда частное решение \({\mathbf{X}_2}\) ищем в виде постоянного вектора: \[{\mathbf{X}_2} = \left( {\begin{array}{*{20}{c}} G\\ H \end{array}} \right).\] После подстановки решения в систему с неоднородной частью \({\mathbf{F}_2}\) получаем: \[ {{\mathbf{X'}_2} = K{\mathbf{X}_2} + {\mathbf{F}_2},}\;\; {\Rightarrow \mathbf{0} = \left( {\begin{array}{*{20}{c}} { - \frac{7}{{10}}}&{\frac{2}{{10}}}\\ {\frac{2}{{10}}}&{ - \frac{7}{{10}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} G\\ H \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{f_0}}\\ 0 \end{array}} \right),}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{c}} { - \frac{7}{{10}}G + \frac{2}{{10}}H + {f_0} = 0}\\ {\frac{2}{{10}}G - \frac{7}{{10}}H = 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{c}} { - 7G + 2H + 10{f_0} = 0}\\ {2G - 7H = 0} \end{array}} \right.,}\;\; {\Rightarrow H = \frac{4}{9}{f_0},\;\;G = \frac{{14}}{9}{f_0}.} \] Таким образом, частное решение \({\mathbf{X}_2}\) представляется следующим постоянным вектором: \[{\mathbf{X}_2} = \left( {\begin{array}{*{20}{c}} {{x_2}}\\ {{y_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} G\\ H \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{{14}}{9}{f_0}}\\ {\frac{4}{9}{f_0}} \end{array}} \right).\] В соответствии с принципом суперпозиции частное решение линейной системы, неоднородная часть которой является суммой векторов \({\mathbf{F}_1}\left( t \right) + {\mathbf{F}_2},\) выражается в виде суммы соответствующих частных решений \({\mathbf{X}_1}\left( t \right) + {\mathbf{X}_2}.\) В результате общее решение задачи записывается как \[ {\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {x\left( t \right)}\\ {y\left( t \right)} \end{array}} \right) = {\mathbf{X}_0}\left( t \right) + {\mathbf{X}_1}\left( t \right) + {\mathbf{X}_2} } = {{C_1}{e^{ - {\large\frac{9}{{10}}\normalsize} t}}\left( {\begin{array}{*{20}{c}} { - 1}\\ 1 \end{array}} \right) + {C_2}{e^{ - {\large\frac{1}{2}\normalsize} t}}\left( {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right) } + {\left( {\begin{array}{*{20}{c}} {10 + 6.55\sin \left( {\frac{\pi }{{12}}t} \right) - 3.55\cos \left( {\frac{\pi }{{12}}t} \right)}\\ {10 + 7.58\sin \left( {\frac{\pi }{{12}}t} \right) - 3.85\cos \left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\frac{{14}}{9}{f_0}}\\ {\frac{4}{9}{f_0}} \end{array}} \right).} \] Найдем постоянные числа \({C_1},\) \({C_2}\) из начальных условий. Пусть, например, \(x\left( 0 \right) = 10^\circ\text{C},\) \(y\left( 0 \right) = 5^\circ\text{C}.\) Следовательно, \[ {\left\{ \begin{array}{l} x\left( 0 \right) = - {C_1} + {C_2} + 10 - 3.55 + \frac{{14}}{9}{f_0} = 10\\ y\left( 0 \right) = {C_1} + {C_2} + 10 - 3.85 + \frac{4}{9}{f_0} = 5 \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} { - {C_1} + {C_2} = 3.55 - 1.56{f_0}}\\ {{C_1} + {C_2} = - 1.55 - 0.44{f_0}} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{C_1} = - 2.35 + 0.56{f_0}}\\ {{C_2} = 1.20 - {f_0}} \end{array}} \right..} \] Окончательное общее решение с учетом заданных начальных условий и при произвольном постоянном уровне источника тепла записывается в таком виде: \[ {\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {x\left( t \right)}\\ {y\left( t \right)} \end{array}} \right) } = {\left( { - 2.35 + 0.56{f_0}} \right){e^{ - {\large\frac{9}{{10}}\normalsize}t}}\left( {\begin{array}{*{20}{c}} { - 1}\\ 1 \end{array}} \right) + \left( {1.20 - {f_0}} \right){e^{ - {\large\frac{1}{2}\normalsize} t}}\left( {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right) } + {\left( {\begin{array}{*{20}{c}} {10 + 6.55\sin \left( {\frac{\pi }{{12}}t} \right) - 3.55\cos \left( {\frac{\pi }{{12}}t} \right)}\\ {10 + 7.58\sin \left( {\frac{\pi }{{12}}t} \right) - 3.85\cos \left( {\frac{\pi }{{12}}t} \right)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {1.56}\\ {0.44} \end{array}} \right){f_0}.} \] Здесь первые два слагаемых являются затухающими членами и описывают переходный процесс. Третье слагаемое обусловлено теплообменом с окружающей средой. Напомним, что в данной задаче был выбран следующий закон изменения наружной температуры: \[{T_e}\left( t \right) = 10 + 10\sin \left( {\frac{\pi }{{12}}t} \right).\] Наконец, последнее слагаемое в общей формуле описывает действие внутреннего постоянного источника тепла \({f_0}.\) Параметр \({f_0}\) пропорционален мощности источника. Включенный источник обеспечивает в течение часа повышение температуры (на нижнем этаже) на \({f_0}\) градусов. Рассмотрим графики изменения температуры. На рисунке \(2\) показаны кривые изменения температуры на нижнем и верхнем этажах дома (соответственно, функции \(x\left( t \right)\) и \(y\left( t \right)\) при выключенном источнике \({f_0} = 0.\) Видно, что при увеличении наружной температуры \({T_e}\left( t \right)\) температура внутри дома изменяется с запаздыванием. Инерция теплообмена приводит также к тому, что температура на нижнем этаже изменяется в интервале от \(2.5^\circ\text{C}\) до \(17.5^\circ\text{C},\) а на верхнем этаже − от \(1.5^\circ\text{C}\) до \(18.5^\circ\text{C},\) в то время как наружная температура изменяется от \(0^\circ\text{C}\) до \(20^\circ\text{C}.\) При включении источника тепла \({f_0}\) в доме, естественно, становится теплее. На рисунке \(3\) показаны графики \(x\left( t \right),\) \(y\left( t \right)\) для случая \({f_0} = 5\left( {\large\frac{\text{град}}{\text{час}}\normalsize} \right).\) Теперь на нижнем этаже температура изменяется от \(10^\circ\text{C}\) до \(25^\circ\text{C},\) а на верхнем − от \(5^\circ\text{C}\) до \(20.5^\circ\text{C}.\) При увеличении мощности источника тепла нижний этаж обогревается значительно лучше, чем верхний этаж (рисунок \(4\)). Исследуя решения \(x\left( t \right),\) \(y\left( t \right)\) при различных режимах работы источника тепла, можно подобрать наиболее комфортный и экономичный режим отопления дома. |
||||||||||||