|
Основные понятия теории устойчивости
|
||||||||||||
|
Предположим, что некоторое явление описывается системой \(n\) дифференциальных уравнений \[\frac{{d{x_i}}}{{dt}} = {f_i}\left( {t,{x_1},{x_2}, \ldots ,{x_n}} \right),\;\;i = 1,2, \ldots ,n\] с начальными условиями \[{x_i}\left( {{t_0}} \right) = {x_{i0}},\;\;i = 1,2, \ldots ,n.\] Будем считать, что функции \({f_i}\left( {t,{x_1},{x_2}, \ldots ,{x_n}} \right)\) определены и непрерывны вместе со своими частными производными на множестве \(\left\{ {t \in \left[ {{t_0}, + \infty } \right),{x_i} \in {\Re^n}} \right\}.\) Далее без ограничения общности полагаем, что начальный момент равен нулю: \({t_0} = 0.\)
Систему дифференциальных уравнений удобнее записать в векторной форме: \[ {\mathbf{X'} = \mathbf{f}\left( {t,\mathbf{X}} \right),\;\;\text{где}}\;\; {\mathbf{X} = \left( {{x_1},{x_2}, \ldots ,{x_n}} \right),}\;\; {\mathbf{f} = \left( {{f_1},{f_2}, \ldots ,{f_n}} \right).} \] В реальных системах начальные условия задаются с определенной точностью. Поэтому возникает естественный вопрос: как малые изменения начальных условий влияют на поведение решения при больших временах - в предельном случае при \(t \to \infty?\) Если траектория движения системы мало изменяется при малых возмущениях начального положения, то говорят, что движение системы является устойчивым. Строгое определение устойчивости в терминах \(\varepsilon - \delta\)-нотации было предложено в \(1892\) году русским математиком А.М.Ляпуновым (\(1857-1918\)). Рассмотрим более подробно понятие устойчивости, введенное Ляпуновым.
Устойчивость по Ляпунову
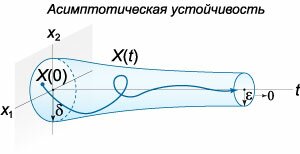
Решение \(\boldsymbol{\varphi} \left( t \right)\) системы дифференциальных уравнений \[\mathbf{X'} = \mathbf{f}\left( {t,\mathbf{X}} \right)\] с начальными условиями \[\mathbf{X}\left( 0 \right) = {\mathbf{X}_0}\] устойчиво (в смысле Ляпунова), если для любого \(\varepsilon > 0\) найдется число \(\delta = \delta \left( \varepsilon \right) > 0,\) такое, что если \[ {\left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\| < \delta ,}\;\; {\text{то}\;\;\left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| < \varepsilon } \] для всех значений \(t \ge 0.\) В противном случае решение \(\boldsymbol{\varphi} \left( t \right)\) называется неустойчивым.В качестве нормы для измерения расстояния между точками можно использовать, например, эвклидову метрику \(\left\| {{\mathbf{x}_e}} \right\|\) или метрику Манхеттена \(\left\| {{\mathbf{x}_m}} \right\|:\) \[\left\| {{\mathbf{x}_e}} \right\| = \sqrt {\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^2}} } ,\;\;\left\| {{\mathbf{x}_m}} \right\| = \sum\limits_{i = 1}^n {\left| {{x_i}} \right|} .\] В случае \(n = 2\) устойчивость по Ляпунову означает, что любая траектория \({\mathbf{X}\left( t \right)},\) которая начинается в \(\delta \left( \varepsilon \right)\)-окрестности точки \({\boldsymbol{\varphi} \left( 0 \right)},\) остается внутри трубки с максимальным радиусом \(\varepsilon\) при всех \(t \ge 0\) (рисунок \(1\)).
Асимптотическая и экспоненциальная устойчивость
Если решение \(\boldsymbol{\varphi} \left( t \right)\) системы дифференциальных уравнений не только устойчиво в смысле Ляпунова, но и удовлетворяет соотношению \[\lim\limits_{t \to \infty } \left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| = 0\] при условии \[\left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\| < \delta,\] то говорят, что решение \(\boldsymbol{\varphi} \left( t \right)\) является асимптотически устойчивым. В этом случае все решения, достаточно близкие к \(\boldsymbol{\varphi} \left( 0 \right)\) в начальный момент времени, постепенно сходятся к \(\boldsymbol{\varphi} \left( t \right)\) при увеличении \(t.\) Схематически это показано на рисунке \(2.\)Если решение \(\boldsymbol{\varphi} \left( t \right)\) асимптотически устойчиво и, кроме того, из условия \[\left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\| < \delta\] следует, что \[\left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| \le \alpha \left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\|{e^{ - \beta t}}\] для всех \(t \ge 0,\) то говорят, что решение \(\boldsymbol{\varphi} \left( t \right)\) является экспоненциально устойчивым. В таком случае все решения, близкие к \(\boldsymbol{\varphi} \left( 0 \right)\) в начальный момент, сходятся к \(\boldsymbol{\varphi} \left( t \right)\) со скоростью (большей или равной), которая определяется экспоненциальной функцией с параметрами \(\alpha,\) \(\beta\) (рисунок \(3\)). Общая теория устойчивости, помимо устойчивости в смысле Ляпунова, содержит много других концепций и определений устойчивого движения. В частности, важное значение имеют понятия орбитальной и структурной устойчивости.
Орбитальная устойчивость
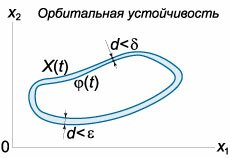
Орбитальная устойчивость описывает поведение замкнутой траектории (орбиты) под действием малых внешних возмущений.Рассмотрим автономную систему \[ {\frac{{d{x_i}}}{{dt}} = {f_i}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),}\;\; {{x_i}\left( {{t_0}} \right) = {x_{i0}},}\;\; {i = 1,2, \ldots ,n,} \] т.е. систему уравнений, правая часть которых не содержит в явном виде независимой переменной \(t.\) В векторном виде автономная система записывается как \[ {\mathbf{X'}\left( t \right) = \mathbf{f}\left( \mathbf{X} \right),\;\;\text{где}}\;\; {\mathbf{X} = \left( {{x_1},{x_2}, \ldots ,{x_n}} \right),}\;\; {\mathbf{f} = \left( {{f_1},{f_2}, \ldots ,{f_n}} \right).} \] Пусть \(\boldsymbol{\varphi} \left( t \right)\) − периодическое решение заданной автономной системы, т.е. имеет вид замкнутой траектории (орбиты). Если для любого \(\varepsilon > 0\) найдется постоянное число \(\delta = \delta \left( \varepsilon \right) > 0,\) такое, что траектория всякого решения \(\mathbf{X}\left( t \right),\) начинающегося в \(\delta\)-окрестности траектории \(\boldsymbol{\varphi} \left( t \right),\) остается в \(\varepsilon\)-окрестности траектории \(\boldsymbol{\varphi} \left( t \right)\) при всех \(t \ge 0,\) то такая траектория \(\boldsymbol{\varphi} \left( t \right)\) называется орбитально устойчивой (рисунок \(4\)). По аналогии с асимптотической устойчивостью в смысле Ляпунова вводится также понятие асимптотической орбитальной устойчивости. Такой тип движения реализуется, например, в системах, имеющих предельный цикл.
Структурная устойчивость
Предположим, что у нас имеются две автономных системы с близкими свойствами - в том смысле, что их фазовые портреты содержат одинаковые особые точки и геометрически похожие траектории. Такие системы можно назвать структурно устойчивыми.В строгом определении требуется, чтобы данные системы были орбитально топологически эквивалентными, т.е. должен существовать гомеоморфизм (это страшное слово означает взаимно-однозначное и непрерывное отображение), который преобразует семейство траекторий первой системы в семейство траекторий второй системы с сохранением направления движения. В этих терминах определение структурной устойчивости формулируется следующим образом. Рассмотрим автономную систему, которая в невозмущенном и возмущенном состоянии описывается, соответственно, двумя уравнениями: \[\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right),\] \[\mathbf{X'} = \mathbf{f}\left( \mathbf{X} \right) + \varepsilon\mathbf{g}\left( \mathbf{X} \right).\] Если для любой ограниченной и непрерывно-дифференцируемой векторной функции \(\mathbf{g}\left( \mathbf{X} \right)\) существует число \(\varepsilon > 0,\) такое, что траектории невозмущенной и возмущенной системы являются орбитально топологически эквивалентными, то такая система называется структурно устойчивой.
Редукция к задаче об устойчивости нулевого решения
Пусть задана произвольная неавтономная система \[\mathbf{X'} = \mathbf{f}\left( {t,\mathbf{X}} \right)\] с начальным условием \(\mathbf{X}\left( 0 \right) = {\mathbf{X}_0}\) (задача Коши), где вектор-функция \(\mathbf{f}\) определена на множестве \(\left\{ {t \in \left[ {{t_0}, + \infty } \right),{x_i} \in {\Re^n}} \right\}.\)Предположим, что данная система имеет решение \(\boldsymbol{\varphi} \left( t \right),\) устойчивость которого требуется исследовать. Анализ устойчивости упрощается, если рассмотреть возмущения \[\mathbf{Z}\left( t \right) = \mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right),\] для которых получается дифференциальное уравнение \[\mathbf{Z'}\left( t \right) = \mathbf{f}\left( {t,\mathbf{Z}} \right).\] Очевидно, что последнему уравнению удовлетворяет нулевое решение \[\mathbf{Z}\left( {t,\mathbf{0}} \right) \equiv \mathbf{0},\] что соответствует тождеству \[\mathbf{X}\left( t \right) \equiv \boldsymbol{\varphi} \left( t \right).\] Таким образом, исследование устойчивости решения \(\boldsymbol{\varphi} \left( t \right)\) можно заменить на исследование устойчивости функции \(\mathbf{Z}\left( t \right)\) вблизи точки \(\mathbf{Z} = \mathbf{0}.\)
Устойчивость линейных систем
Линейная система \[\mathbf{X'} = A\left( t \right)\mathbf{X} + \mathbf{f}\left( t \right)\] называется устойчивой, если все ее решения устойчивы в смысле Ляпунова.Оказывается, что неоднородная линейная система будет устойчивой при любом свободном члене \(\mathbf{f}\left( t \right),\) если устойчиво нулевое решение соответствующей однородной системы \[\mathbf{X'} = A\left( t \right)\mathbf{X}.\] Поэтому при изучении устойчивости в классе линейных систем достаточно ограничиться анализом однородных дифференциальных систем. В наиболее простом случае, когда матрица коэффициентов \(A\) является постоянной, условия устойчивости формулируются в терминах собственных значений матрицы \(A.\) Рассмотрим однородную линейную систему \[\mathbf{X'} = A\mathbf{X},\] где \(A\) − постоянная матрица размером \(n \times n.\) Такая система (она также является автономной) имеет нулевое решение \(\mathbf{X}\left( t \right) = \mathbf{0}.\) Устойчивость данного решения определяется следующими теоремами. Пусть \({\lambda _i}\) − собственные числа матрицы \(A.\) Теорема \(1\). Линейная однородная система с постоянными коэффициентами устойчива в смысле Ляпунова тогда и только тогда, когда все собственные значения \({\lambda _i}\) матрицы \(A\) удовлетворяют соотношению \[\text{Re}\left[ {{\lambda _i}} \right] \le 0\;\;\left( {i = 1,2, \ldots ,n} \right),\] причем у собственных значений, действительная часть которых равна нулю, алгебраическая и геометрическая кратность должны быть одинаковы (т.е. соответствующие жордановы клетки должны быть размера \(1 \times 1.\)) Теорема \(2\). Линейная однородная система с постоянными коэффициентами является асимптотически устойчивой тогда и только тогда, когда все собственные значения \({\lambda _i}\) имеют отрицательные действительные части: \[\text{Re}\left[ {{\lambda _i}} \right] \lt 0\;\;\left( {i = 1,2, \ldots ,n} \right).\] Теорема \(3\). Линейная однородная система с постоянными коэффициентами неустойчива, если выполнено хотя бы одно из условий:
Устойчивость по первому приближению
Рассмотрим нелинейную автономную систему \(\mathbf{X'} = f\left( \mathbf{X} \right).\) Предположим, что система имеет нулевое решение \(\mathbf{X} = \mathbf{0},\) которое будем исследовать на устойчивость.Считая функции \({f_i}\left( \mathbf{X} \right)\) дважды непрерывно дифференцируемыми в некоторой окрестности начала координат, можно разложить правую часть в ряд Маклорена: \[ {\frac{{d{x_1}}}{{dt}} = \frac{{\partial {f_1}}}{{\partial {x_1}}}\left( 0 \right){x_1} + \frac{{\partial {f_1}}}{{\partial {x_2}}}\left( 0 \right){x_2} + \cdots } + {\frac{{\partial {f_1}}}{{\partial {x_n}}}\left( 0 \right){x_n} } + {{R_1}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),} \] \[ {\frac{{d{x_2}}}{{dt}} = \frac{{\partial {f_2}}}{{\partial {x_1}}}\left( 0 \right){x_1} + \frac{{\partial {f_2}}}{{\partial {x_2}}}\left( 0 \right){x_2} + \cdots } + {\frac{{\partial {f_2}}}{{\partial {x_n}}}\left( 0 \right){x_n} } + {{R_2}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),} \] \[\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\] \[ {\frac{{d{x_n}}}{{dt}} = \frac{{\partial {f_n}}}{{\partial {x_1}}}\left( 0 \right){x_1} + \frac{{\partial {f_n}}}{{\partial {x_2}}}\left( 0 \right){x_2} + \cdots } + {\frac{{\partial {f_n}}}{{\partial {x_n}}}\left( 0 \right){x_n} } + {{R_n}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right).} \] где слагаемые \({R_i}\) описывают члены второго (и более высокого) порядка малости относительно координатных функций \({{x_1},{x_2}, \ldots ,{x_n}}.\) Возвращаясь к векторно-матричной записи, получаем: \[\mathbf{X'} = J\mathbf{X} + \mathbf{R}\left( \mathbf{X} \right),\] где якобиан \(J\) определяется формулой \[J = \left( {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}}}{{\partial {x_1}}}}&{\frac{{\partial {f_1}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_1}}}{{\partial {x_n}}}}\\ {\frac{{\partial {f_2}}}{{\partial {x_1}}}}&{\frac{{\partial {f_2}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_2}}}{{\partial {x_n}}}}\\ \cdots & \cdots & \vdots & \cdots \\ {\frac{{\partial {f_n}}}{{\partial {x_1}}}}&{\frac{{\partial {f_n}}}{{\partial {x_2}}}}& \vdots &{\frac{{\partial {f_n}}}{{\partial {x_n}}}} \end{array}} \right).\] Значения частных производных в этой матрице вычисляются в точке разложения в ряд, т.е. в данном случае в нуле. Во многих случаях вместо исходной нелинейной автономной системы можно рассматривать и исследовать на устойчивость соответствующую линеаризованную систему или систему уравнений первого приближения. Устойчивость такой системы определяется следующими признаками:
Функции Ляпунова
Одним из мощных инструментов анализа устойчивости систем дифференциальных уравнений, включая нелинейные системы, являются функции Ляпунова. Данная техника подробно рассматривается на отдельной web-странице "Метод функций Ляпунова". |
||||||||||||
|
Пример 1
|
||||||||||||
|
Используя определение устойчивости по Ляпунову, показать, что нулевое решение системы устойчиво. \[\frac{{dx}}{{dt}} = - x - y,\;\;\frac{{dy}}{{dt}} = - x + y.\]
Решение.
Сначала найдем общее решение системы. Собственные значения \({\lambda _i}\) матрицы коэффициентов \(A\) равны: \[ {A = \left( {\begin{array}{*{20}{r}} { - 1}&{ - 1}\\ 1&1 \end{array}} \right),}\;\; {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - 1 - \lambda }&{ - 1}\\ 1&{1 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\left( { - 1 - \lambda } \right)^2} + 1 = 0,}\;\; {\Rightarrow {\lambda ^2} + 2\lambda + 2 = 0,}\;\; {\Rightarrow {\lambda _{1,2}} = - 1 \pm i.} \] Определим собственный вектор \({\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}\) для собственного значения \({\lambda _1} = - 1 + i:\) \[ {\left( {A - {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - 1 - \left( { - 1 + i} \right)}&{ - 1}\\ 1&{ - 1 - \left( { - 1 + i} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} { - i}&{ - 1}\\ 1&{ - i} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} { - i{V_{11}} - {V_{21}} = 0}\\ {{V_{11}} - i{V_{21}} = 0} \end{array}} \right..} \] Полученные уравнения являются линейно зависимыми. Поэтому, полагая \({V_{21}} = t,\) из второго уравнения находим: \[{V_{11}} = i{V_{21}} = it.\] Следовательно, собственный вектор \({\mathbf{V}_1}\) равен: \[ {{\mathbf{V}_1} = \left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {it}\\ t \end{array}} \right) } = {t\left( {\begin{array}{*{20}{c}} i\\ 1 \end{array}} \right) } \sim {\left( {\begin{array}{*{20}{c}} i\\ 1 \end{array}} \right).} \] Тогда решение \({\mathbf{X}_1}\left( t \right),\) соответствующее комплексному числу \({\lambda _1} = - 1 + i,\) имеет вид: \[ {{\mathbf{X}_1}\left( t \right) = \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) = {e^{{\lambda _1}t}}{\mathbf{V}_1} } = {{e^{\left( { - 1 + i} \right)t}}\left( {\begin{array}{*{20}{c}} i\\ 1 \end{array}} \right).} \] Разложим экспоненциальную функцию по формуле Эйлера: \[ {{e^{\left( { - 1 + i} \right)t}} = {e^{ - t}}{e^{it}} } = {{e^{ - t}}\left( {\cos t + i\sin t} \right).} \] Получаем \[ {{\mathbf{X}_1}\left( t \right) = \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) } = {{e^{ - t}}\left( {\cos t + i\sin t} \right)\left( {\begin{array}{*{20}{c}} i\\ 1 \end{array}} \right) } = {{e^{ - t}}\left( {\begin{array}{*{20}{c}} {\left( {\cos t + i\sin t} \right)i}\\ {\cos t + i\sin t} \end{array}} \right) } = {{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - \sin t + i\cos t}\\ {\cos t + i\sin t} \end{array}} \right) } = {{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - \sin t}\\ {\cos t} \end{array}} \right) + i{e^{ - t}}\left( {\begin{array}{*{20}{c}} {\cos t}\\ {\sin t} \end{array}} \right).} \] Отсюда видно, что действительная и мнимая части решения равны \[ {\text{Re}\left[ {{\mathbf{X}_1}\left( t \right)} \right] = {e^{ - t}}\left( {\begin{array}{*{20}{c}} { - \sin t}\\ {\cos t} \end{array}} \right),}\;\; {\text{Im}\left[ {{\mathbf{X}_1}\left( t \right)} \right] = {e^{ - t}}\left( {\begin{array}{*{20}{c}} {\cos t}\\ {\sin t} \end{array}} \right).} \] Следовательно, общее решение системы выражается формулой \[ {\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) } = {{C_1}{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - \sin t}\\ {\cos t} \end{array}} \right) } + {{C_2}{e^{ - t}}\left( {\begin{array}{*{20}{c}} {\cos t}\\ {\sin t} \end{array}} \right)} \] или \[\left\{ \begin{array}{l} x\left( t \right) = - {C_1}{e^{ - t}}\sin t + {C_2}{e^{ - t}}\cos t\\ y\left( t \right) = {C_1}{e^{ - t}}\cos t + {C_2}{e^{ - t}}\sin t \end{array} \right..\] Полагая, что в начальный момент \(t = 0\) система находится в точке \(\left( {{x_0},{y_0}} \right),\) получаем: \[\left\{ \begin{array}{l} x\left( 0 \right) = {C_2} = {x_0}\\ y\left( 0 \right) = {C_1} = {y_0} \end{array} \right..\] С учетом этого решение можно записать в следующем виде: \[\left\{ \begin{array}{l} x\left( t \right) = - {y_0}{e^{ - t}}\sin t + {x_0}{e^{ - t}}\cos t\\ y\left( t \right) = {y_0}{e^{ - t}}\cos t + {x_0}{e^{ - t}}\sin t \end{array} \right..\] Траектория этого решения выходит из точки \(\left( {{x_0},{y_0}} \right).\)Теперь исследуем устойчивость нулевого решения, которое обозначим как \(\boldsymbol{\varphi} \left( t \right) \equiv 0.\) Согласно определению устойчивости по Ляпунову введем некоторое число \(\varepsilon > 0\) и найдем соответствующее ему число \(\delta = \delta \left( \varepsilon \right) > 0,\) такое, что при \[\left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\| < \delta \] будет выполняться соотношение \[\left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| < \varepsilon \] для всех \(t \ge 0.\) Пусть возмущенное решение \(\mathbf{X}\left( t \right)\) в начальный момент имеет координаты \(\left( {{x_0},{y_0}} \right).\) Считая, что отклонение от нуля по каждой из координат не превосходит \(\large\frac{\delta }{2}\normalsize\) и применяя неравенство треугольника, можно записать: \[ {\left\| {\mathbf{X}\left( 0 \right) - \boldsymbol{\varphi} \left( 0 \right)} \right\| } = {\sqrt {{{\left| {{x_0}} \right|}^2} + {{\left| {{y_0}} \right|}^2}} \le \left| {{x_0}} \right| + \left| {{y_0}} \right| } = {\frac{\delta }{2} + \frac{\delta }{2} = \delta .} \] Здесь в качестве нормы мы использовали обычную эвклидову метрику. Установим связь между числами \(\delta\) и \(\varepsilon.\) Подставляя известные выражения для решения \(\mathbf{X}\left( t \right) = \left( {x\left( t \right),y\left( t \right)} \right),\) получаем: \[ {\left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| } = {{e^{ - t}}\sqrt {{{\left| { - {y_0}\sin t + {x_0}\cos t} \right|}^2} + {{\left| {{y_0}\cos t + {x_0}\sin t} \right|}^2}} } \le {{e^{ - t}}\sqrt {{{\left( {\left| {{y_0}} \right| + \left| {{x_0}} \right|} \right)}^2} + {{\left( {\left| {{y_0}} \right| + \left| {{x_0}} \right|} \right)}^2}} } = {{e^{ - t}}\sqrt {2{{\left( {\left| {{y_0}} \right| + \left| {{x_0}} \right|} \right)}^2}} } = {{e^{ - t}}\sqrt {2{{\left( {\frac{\delta }{2} + \frac{\delta }{2}} \right)}^2}} } = {{e^{ - t}}\sqrt {2{\delta ^2}} } = {\sqrt 2 {e^{ - t}}\delta \le \sqrt 2 \delta = \varepsilon .} \] Итак, если мы положим \(\delta = \large\frac{\varepsilon }{{\sqrt 2 }}\normalsize,\) то все возмущенные траектории, выходящие из точки \(\left( {{x_0},{y_0}} \right),\) при условии \(\left| {{x_0}} \right| < \large\frac{\delta }{2}\normalsize,\;\left| {{y_0}} \right| < \large\frac{\delta }{2}\normalsize,\) будут оставаться в трубке с радиусом \(\varepsilon.\) Таким образом, система является устойчивой в смысле Ляпунова. Заметим, что на самом деле выполняется более сильное условие: \[\lim\limits_{t \to \infty } \left\| {\mathbf{X}\left( t \right) - \boldsymbol{\varphi} \left( t \right)} \right\| = \lim\limits_{t \to \infty } \left( {\sqrt 2 {e^{ - t}}\delta } \right) = 0.\] т.е. система является асимптотически устойчивой. |
||||||||||||
|
Пример 2
|
||||||||||||
|
Исследовать на устойчивость и асимптотическую устойчивость нулевое решение системы, общее решение которой имеет вид \[\left\{ \begin{array}{l} x\left( t \right) = 3{C_1} + {C_2}{e^{ - t}}\\ y\left( t \right) = 2{C_1}{t^2}{e^{ - t}} - {C_2}\cos t \end{array} \right..\]
Решение.
Пусть начальные условия заданы в виде \(x\left( 0 \right) = {x_0},y\left( 0 \right) = {y_0}.\) Выразим общее решение системы через координаты \({x_0},{y_0}:\) \[ {\left\{ \begin{array}{l} x\left( 0 \right) = 3{C_1} = {x_0}\\ y\left( 0 \right) = - {C_2} = {y_0} \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{C_1} = \frac{{{x_0}}}{3}}\\ {{C_2} = - {y_0}} \end{array}} \right..} \] Тогда \[\left\{ \begin{array}{l} x\left( t \right) = {x_0} - {y_0}{e^{ - t}}\\ y\left( t \right) = \frac{2}{3}{x_0}{t^2}{e^{ - t}} + {y_0}\cos t \end{array} \right..\] Предположим, что решения \(x\left( t \right),y\left( t \right)\) при всех значениях \(t \ge 0\) удовлетворяют соотношениям \[\left| {x\left( t \right)} \right| < \varepsilon ,\;\;\left| {y\left( t \right)} \right| < \varepsilon ,\] где \(\varepsilon\) − произвольное положительное число. В соответствии с определением устойчивости по Ляпунову попробуем подобрать число \(\delta \left( \varepsilon \right),\) зависящее от \(\varepsilon,\) такое, чтобы выполнялись неравенства \[ {\left| {x\left( 0 \right)} \right| = \left| {{x_0}} \right| < \delta \left( \varepsilon \right),}\;\; {\left| {y\left( 0 \right)} \right| = \left| {{y_0}} \right| < \delta \left( \varepsilon \right).} \] В результате получаем \[ {\left| {x\left( t \right)} \right| = \left| {{x_0} - {y_0}{e^{ - t}}} \right| } \le {\left| {{x_0}} \right| + \left| {{y_0}} \right| < \varepsilon ,} \] \[ {\left| {y\left( t \right)} \right| = \left| {\frac{2}{3}{x_0}{t^2}{e^{ - t}} + {y_0}\cos t} \right| } \le {\frac{2}{3}\left| {{x_0}} \right|{t^2}{e^{ - t}} + \left| {{y_0}} \right| < \varepsilon .} \] Учтем, что функция \(g\left( t \right) = {t^2}{e^{ - t}}\) является ограниченной. Действительно, \[ {g'\left( t \right) = {\left( {{t^2}{e^{ - t}}} \right)^\prime } } = {2t{e^{ - t}} - {t^2}{e^{ - t}} } = {\left( {2t - {t^2}} \right){e^{ - t}} } = {t\left( {2 - t} \right){e^{ - t}},}\;\; {\Rightarrow g'\left( t \right) = 0\;\;\text{при}\;\;t = 0,2.} \] При \(t = 2\) функция \(g\left( t \right) = {t^2}{e^{ - t}}\) имеет максимум, равный \[ {{g_{\max }} = g\left( {t = 2} \right) } = {{2^2}{e^{ - 2}} } \approx {0.54 < 1.} \] Тогда неравенство для \(\left| {y\left( t \right)} \right|\) записывается в виде \[\left| {y\left( t \right)} \right| \le \frac{2}{3}\left| {{x_0}} \right| + \left| {{y_0}} \right| < \varepsilon .\] Если мы теперь выберем \(\delta = \large\frac{\varepsilon }{2}\normalsize,\) так что \[ {\left| {{x_0}} \right| < \delta = \frac{\varepsilon }{2}\;\;\text{и}}\;\; {\left| {{y_0}} \right| < \delta = \frac{\varepsilon }{2},} \] то будут заведомо выполняться неравенства \[ {\left| {x\left( t \right)} \right| = \left| {{x_0}} \right| + \;\left| {{y_0}} \right| < \frac{\varepsilon }{2} + \frac{\varepsilon }{2} = \varepsilon ,}\;\; {\left| {y\left( t \right)} \right| \le \frac{2}{3}\left| {{x_0}} \right| + \left| {{y_0}} \right| < \frac{2}{3} \cdot \frac{\varepsilon }{2} + \frac{\varepsilon }{2} } = {\frac{{5\varepsilon }}{6} < \varepsilon .} \] Следовательно, нулевое решение заданной системы уравнений устойчиво.Из формул для \({x\left( t \right)},{y\left( t \right)} \) видно, что система не является асимптотически устойчивой, поскольку при \(t \to \infty\) значения \({x\left( t \right)},{y\left( t \right)} \) не стремятся к нулю. |
||||||||||||
|
Пример 3
|
||||||||||||
|
Определить, при каких значениях параметров \(a, b\) нулевое решение системы \[\frac{{dx}}{{dt}} = ax + y,\;\;\frac{{dy}}{{dt}} = x + by\] является асимптотически устойчивым?
Решение.
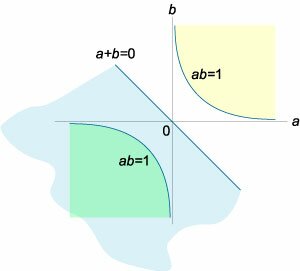
Вычислим собственные значения \({\lambda _i}\) матрицы коэффициентов \(A:\) \[ {A = \left( {\begin{array}{*{20}{c}} a&1\\ 1&b \end{array}} \right),}\;\; {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {a - \lambda }&1\\ 1&{b - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( {a - \lambda } \right)\left( {b - \lambda } \right) - 1 = 0,}\;\; {\Rightarrow {\lambda ^2} - \left( {a + b} \right)\lambda + ab - 1 = 0.} \] Решим полученное квадратное уравнение с параметрами \(a, b.\) \[ {D = {\left( {a + b} \right)^2} - 4\left( {ab - 1} \right) } = {{a^2} + 2ab + {b^2} - 4ab + 4 } = {{a^2} - 2ab + {b^2} + 4 } = {{\left( {a - b} \right)^2} + 4 > 0.} \] Как видно, дискриминант всегда положительный. Поэтому собственные значения являются действительными числами и определяются формулой \[{\lambda _{1,2}} = \frac{{a + b \pm \sqrt {{{\left( {a - b} \right)}^2} + 4} }}{2}.\] Найдем множество значений чисел \(a, b\) при которых собственные значения \({\lambda _1},\) \({\lambda _2}\) отрицательны (что соответствует условию асимптотической устойчивости системы): \[\left\{ \begin{array}{l} {\lambda _1} < 0\\ {\lambda _2} < 0 \end{array} \right.,\;\; \Rightarrow \left\{ {\begin{array}{*{20}{c}} {a + b + \sqrt {{{\left( {a - b} \right)}^2} + 4} < 0}\\ {a + b - \sqrt {{{\left( {a - b} \right)}^2} + 4} < 0} \end{array}} \right..\] Складывая оба неравенства, получаем \(a + b < 0.\) В таком случае второе неравенство \[\sqrt {{{\left( {a - b} \right)}^2} + 4} > a + b\] выполняется при всех \(a, b,\) удовлетворяющих условию \(a + b < 0.\)Решим первое неравенство: \[ {\left\{ \begin{array}{l} \sqrt {{{\left( {a - b} \right)}^2} + 4} < - \left( {a + b} \right)\\ a + b < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {\left( {a - b} \right)^2} + 4 < {\left( {a + b} \right)^2}\\ a + b < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {\left( {a + b} \right)^2} - {\left( {a + b} \right)^2} > 4\\ a + b < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} \left( {a + b - a + b} \right)\left( {a + b + a - b} \right) > 4\\ a + b < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} 4ab > 4\\ a + b < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} ab > 1\\ a + b < 0 \end{array} \right..} \] Решение обоих элементарных неравенств показаны графически на рисунке \(5.\) Общим решением является область (заштрихованная зеленым цветом), расположенная ниже гиперболы \(ab = 1\) в левой полуплоскости. При всех значениях \(a, b\) из этой области решение системы будет асимптотически устойчивым.
|
||||||||||||