Ортогональные траектории

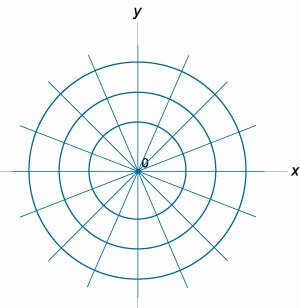
Пусть семейство кривых задано уравнением \[g\left( {x,y} \right) = C,\] где \(C\) − постоянная. Для данного семейства кривых можно построить ортогональные траектории, то есть такое множество кривых \(f\left( {x,y} \right) = C,\) которые будут пересекать исходные кривые под прямым углом.

Например, ортогональной траекторией для пучка прямых линий, заданных уравнением \(y = kx,\) где \(k\) − параметр (наклон прямой), является любая окружность с центром в начале координат (Рисунок \(1\)): \[{x^2} + {y^2} = {R^2},\] где \(R\) − радиус окружности. Аналогично, ортогональными траекториями для семейства эллипсов \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{c^2} - {a^2}}} = 1,\;\;\text{где}\;\;0 < a < c,\] будут являться конфокальные гиперболы, удовлетворяющие уравнению: \[\frac{{{x^2}}}{{{b^2}}} - \frac{{{y^2}}}{{{b^2} - {c^2}}} = 1,\;\;\text{где}\;\;0 < c < b.\] Оба семейства кривых схематически изображены ни рисунке \(2.\) Здесь \(a\) и \(b\) играют роль параметров, описывающих, соответственно, семейство эллипсов и гипербол. Общий подход к определению ортогональных траекторий основан на решении дифференциального уравнения в частных производных: \[\nabla f\left( {x,y} \right) \cdot \nabla g\left( {x,y} \right) = 0,\] где символ \(\nabla\) обозначает градиент функции \(f\left( {x,y} \right)\) или \(g\left( {x,y} \right),\) а точка означает скалярное произведение двух векторов градиента.

Используя определение градиента, можно записать: \[\nabla f\left( {x,y} \right) = \mathbf{grad}\,f\left( {x,y} \right) = \left( {\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}}} \right),\] \[\nabla g\left( {x,y} \right) = \mathbf{grad}\,g\left( {x,y} \right) = \left( {\frac{{\partial g}}{{\partial x}},\frac{{\partial g}}{{\partial y}}} \right).\] Следовательно, данное уравнение в частных производных можно переписать в виде: \[ {\nabla f\left( {x,y} \right) \cdot \nabla g\left( {x,y} \right) = 0,}\;\; {\Rightarrow \left( {\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}}} \right) \cdot \left( {\frac{{\partial g}}{{\partial x}},\frac{{\partial g}}{{\partial y}}} \right) = 0,}\;\; {\Rightarrow \frac{{\partial f}}{{\partial x}}\frac{{\partial g}}{{\partial x}} + \frac{{\partial f}}{{\partial y}}\frac{{\partial g}}{{\partial y}} = 0.} \] Решая последнее уравнение, определяем уравнение ортогональных траекторий \(f\left( {x,y} \right) = C.\) Ниже мы опишем простой алгоритм нахождения ортогональных траекторий \(f\left( {x,y} \right) = C\) для заданного семейства кривых \(g\left( {x,y} \right) = C,\) используя только обыкновенные дифференциальные уравнения. Этот алгоритм включает следующие шаги:

1. Сначала мы определяем дифференциальное уравнение \(G\left( {x,y,y'} \right) = 0\) для заданного семейства кривых \(g\left( {x,y} \right) = C.\) Смотрите подробнее об этом на странице Дифференциальные уравнения плоских кривых.

2. Далее заменяем в дифференциальном уравнении \(y'\) на \(\left( { - \large\frac{1}{{y'}}\normalsize} \right).\) В результате получаем дифференциальное уравнение ортогональных траекторий.

3. Решаем новое дифференциальное уравнение и находим алгебраическое уравнение семейства ортогональных траекторий \(f\left( {x,y} \right) = C.\)

   Пример 1

Найти ортогональные траектории семейства прямых линий \(y = Cx,\) где \(C\) − параметр. Воспользуемся описанным выше алгоритмом.

\(1)\) Запишем дифференциальное уравнение для заданного семейства прямых \(y = Cx.\) Дифференцируя последнее уравнение по переменной \(x,\) получаем: \[y' = C = \text{const}.\] Исключим постоянную \(C\) из системы уравнений: \[\left\{ \begin{array}{l} y = Cx\\ y' = C \end{array} \right.,\;\; \Rightarrow y' = \frac{y}{x}.\] Получаем дифференциальное уравнение для исходного пучка прямых линий.

\(2)\) Заменим \(y'\) на \(\left( { - \large\frac{1}{{y'}}\normalsize} \right).\) В результате находим дифференциальное уравнение ортогональных траекторий: \[ - \frac{1}{{y'}} = \frac{y}{x},\;\; \Rightarrow y' = - \frac{x}{y}.\] \(3)\) Наконец решим полученное дифференциальное уравнение и определим алгебраическое уравнение семейства ортогональных траекторий: \[ {y' = - \frac{x}{y},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = - \frac{x}{y},}\;\; {\Rightarrow ydy = - xdx,}\;\; {\Rightarrow \int {ydy} = - \int {xdx} ,}\;\; {\Rightarrow \frac{{{y^2}}}{2} = - \frac{{{x^2}}}{2} + C,}\;\; {\Rightarrow \frac{{{x^2}}}{2} + \frac{{{y^2}}}{2} = C,}\;\; {\Rightarrow {x^2} + {y^2} = 2C.} \] Заменяя \(2C\) на \({R^2},\) мы видим, что ортогональные траектории для данного семейства прямых представляют собой концентрические окружности (Рисунок \(1\)): \[{x^2} + {y^2} = {R^2}.\]

   Пример 2

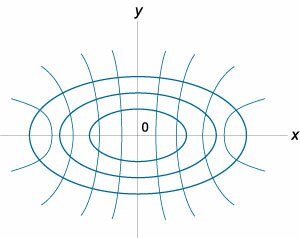
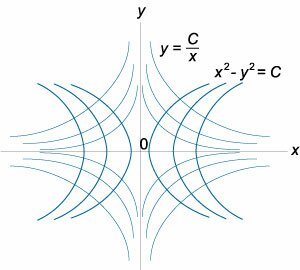
Семейство гиперболических кривых задано уравнением \(y = \large\frac{C}{x}\normalsize.\) Найти ортогональные траектории к этим кривым. \(1)\) Определим дифференциальное уравнение для семейства гипербол. Дифференцируя уравнение по переменной \(x,\) получаем: \[y' = - \frac{C}{{{x^2}}}.\] Исключим параметр \(C\) из системы двух уравнений: \[\left\{ \begin{array}{l} y = \frac{C}{x}\\ y' = - \frac{C}{{{x^2}}} \end{array} \right..\] Из первого уравнения следует, что \(C = xy.\) Подставляя это во второе уравнение, находим: \[y' = - \frac{{xy}}{{{x^2}}} = - \frac{y}{x}.\] \(2)\) Заменим \(y'\) на \(\left( { - \large\frac{1}{{y'}}\normalsize} \right):\) \[ - \frac{1}{{y'}} = - \frac{y}{x},\;\; \Rightarrow y' = \frac{x}{y}.\] \(3)\) Теперь проинтегрируем дифференциальное уравнение, описывающее ортогональные траектории: \[ {y' = \frac{x}{y},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = \frac{x}{y},}\;\; {\Rightarrow ydy = xdx,}\;\; {\Rightarrow \int {ydy} = \int {xdx} ,}\;\; {\Rightarrow \frac{{{y^2}}}{2} = \frac{{{x^2}}}{2} + C,}\;\; {\Rightarrow {x^2} - {y^2} = C.} \] В последнем уравнении мы заменили \(2C\) просто на \(C.\) В итоге мы получили алгебраическое уравнение семейства ортогональных траекторий. Как видно, эти траектории также являются гиперболами. Оба семейства гипербол схематически показаны на рисунке \(3.\)

   Пример 3

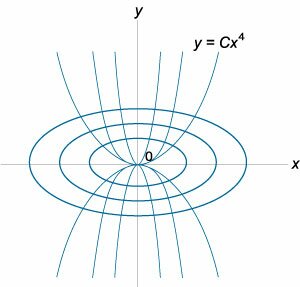
Определить ортогональные траектории для семейства кривых, заданных степенной функцией \(y = C{x^4}.\) \(1)\) Найдем дифференциальное уравнение, соответствующее заданному семейству степенных кривых: \[y = C{x^4},\;\; \Rightarrow y' = 4C{x^3}.\] Решая систему двух уравнений и исключая \(C,\) получаем: \[ {C = \frac{y}{{{x^4}}},}\;\; {\Rightarrow y' = 4 \cdot \frac{y}{{{x^4}}} \cdot {x^3} = \frac{{4y}}{x}.} \] \(2)\) Заменяем \(y'\) на \(\left( { - \large\frac{1}{{y'}}\normalsize} \right):\) \[ - \frac{1}{{y'}} = \frac{{4y}}{x},\;\; \Rightarrow y' = - \frac{x}{{4y}}.\] Последнее выражение представляет собой дифференциальное уравнение ортогональных траекторий.

\(3)\) Интегрируя, можно найти соответствующее алгебраическое уравнение ортогональных траекторий: \[ {y' = - \frac{x}{{4y}},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = - \frac{x}{{4y}},}\;\; {\Rightarrow 4ydy = - xdx,}\;\; {\Rightarrow 4\int {ydy} = - \int {xdx} ,}\;\; {\Rightarrow 4 \cdot \frac{{{y^2}}}{2} = - \frac{{{x^2}}}{2} + C,}\;\; {\Rightarrow 4{y^2} + {x^2} = 2C.} \] Разделим обе части на \(2C:\) \[ {\frac{{4{y^2}}}{{2C}} + \frac{{{x^2}}}{{2C}} = \frac{{2C}}{{2C}},}\;\; {\Rightarrow \frac{{{y^2}}}{{\frac{C}{2}}} + \frac{{{x^2}}}{{2C}} = 1,}\;\; {\Rightarrow \frac{{{y^2}}}{{{{\left( {\sqrt {\frac{C}{2}} } \right)}^2}}} + \frac{{{x^2}}}{{{{\left( {\sqrt {2C} } \right)}^2}}} = 1.} \] Получаем уравнение семейства эллипсов, которые будут ортогональны к заданному семейству степенных кривых \(y = C{x^4}.\) Отношение длин полуосей этих эллипсов равно \[\frac{{\sqrt {2C} }}{{\sqrt {\frac{C}{2}} }} = \frac{{\sqrt 2 }}{{\sqrt {\frac{1}{2}} }} = {\left( {\sqrt 2 } \right)^2} = 2.\] Схематически графики обоих семейств кривых показаны выше на рисунке \(4.\)

   Пример 4

Определить ортогональные траектории для семейства синусоид \(y = C\sin x.\) \(1)\) Продифференцируем заданное уравнение по переменной \(x:\) \[y' = C\cos x.\] Подставляя \(C = \large\frac{y}{{\sin x}}\normalsize,\) находим дифференциальное уравнение, соответствующее синусоидальным кривым: \[y' = \frac{y}{{\sin x}}\cos x = y\cot x.\] \(2)\) Заменяя \(y'\) на \(\left( { - \large\frac{1}{{y'}}\normalsize} \right),\) запишем дифференциальное уравнение ортогональных кривых: \[ {- \frac{1}{{y'}} = y\cot x,}\;\; {\Rightarrow y' = - \frac{1}{{y\cot x}} = - \frac{{\tan x}}{y}.} \] \(3)\) Теперь можно проинтегрировать последнее уравнение: \[ {y' = - \frac{{\tan x}}{y},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = - \frac{{\tan x}}{y},}\;\; {\Rightarrow ydy = - \tan xdx,}\;\; {\Rightarrow \int {ydy} = - \int {\tan xdx} ,}\;\; {\Rightarrow \frac{{{y^2}}}{2} = \ln \left| {\cos x} \right| + \ln C,}\;\; {\Rightarrow \frac{{{y^2}}}{2} = \ln \left( {C\left| {\cos x} \right|} \right).} \] Отсюда следует, что \[ {C\left| {\cos x} \right| = \exp \left( {\frac{{{y^2}}}{2}} \right),}\;\; {\Rightarrow \cos x = \pm \frac{1}{C}\exp \left( {\frac{{{y^2}}}{2}} \right).} \] Обозначив \({C_1} = \pm {\large\frac{1}{C}\normalsize},\) получим окончательное неявное уравнение ортогональных кривых: \[\cos x = {C_1}\exp \left( {\frac{{{y^2}}}{2}} \right).\]