Ортогональные полиномы и обобщенный ряд Фурье

Два полинома, заданные на интервале \(\left[ {a,b} \right],\) являются ортогональными, если выполнено условие \[\int\limits_a^b {p\left( x \right)q\left( x \right)w\left( x \right)dx} = 0,\] где \({w\left( x \right)}\) − неотрицательная весовая функция.

Множество полиномов \({p_n}\left( x \right),\;n = 0,1,2, \ldots ,\) где \(n\) − степень полинома \({p_n}\left( x \right),\) образуют систему ортогональных полиномов, если справедливо равенство \[\int\limits_a^b {{p_m}\left( x \right){p_n}\left( x \right)w\left( x \right)dx} = {c_n}{\delta _{mn}},\] где \({c_n}\) − заданные константы, а \({\delta _{mn}}\) − символ Кронекера. Обобщенным рядом Фурье для некоторой функции называется ее разложение в ряд на основе системы ортогональных полиномов. Любая кусочно непрерывная функция может быть представлена в виде обобщенного ряда Фурье: \[ \sum\limits_{n = 0}^\infty {{c_n}{p_n}\left( x \right)} = \begin{cases} f\left( x \right), & \text{если}\,f\left( x \right)\,\text{непрерывна} \\ \frac{{f\left( {x - 0} \right) + f\left( {x + 0} \right)}}{2}, & \text{в точке разрыва 2 рода} \end{cases}. \] Ниже мы рассмотрим \(4\) вида ортогональных полиномов: полиномы Эрмита, Лагерра, Лежандра и Чебышева. Полиномы Эрмита \({H_n}\left( x \right) = {\left( { - 1} \right)^n}{e^{{x^2}}}\large\frac{{{d^n}}}{{d{x^n}}}\normalsize {e^{ - {x^2}}}\) ортогональны с весовой функцией \({e^{ - {x^2}}}\) на интервале \(\left( { - \infty ,\infty } \right):\) \[ \int\limits_{ - \infty }^\infty {{e^{ - {x^2}}}{H_m}\left( x \right){H_n}\left( x \right)dx} = \begin{cases} 0, & m \ne n \\ {2^n}n!\sqrt \pi, & m = n \end{cases}. \] Иногда используется альтернативное определение, в котором весовая функция равна \({e^{ - \frac{{{x^2}}}{2}}}.\) Это соглашение распространено в теории вероятностей, в частности, из-за того, что плотность нормального распределения описывается функцией \(\large\frac{1}{{\sqrt {2\pi } }}\normalsize {e^{ - \frac{{{x^2}}}{2}}}.\) Полиномы Лагерра \({L_n}\left( x \right) = {\large\frac{{{e^x}}}{{n!}}\normalsize} {\large\frac{{{d^n}\left( {{x^n}{e^{ - x}}} \right)}}{{d{x^n}}}\normalsize},\;n = 0,1,2,3, \ldots \) ортогональны с весовой функцией \({{e^{ - x}}}\) на интервале \(\left( {0,\infty } \right):\) \[ \int\limits_0^\infty {{e^{ - x}}{L_m}\left( x \right){L_n}\left( x \right)dx} = \begin{cases} 0, & m \ne n \\ 1, & m = n \end{cases}. \] Полиномы Лежандра \({P_n}\left( x \right) = {\large\frac{1}{{{2^n}n!}}\normalsize} {\large\frac{{{d^n}{{\left( {{x^2} - 1} \right)}^n}}}{{d{x^n}}}\normalsize},\;n = 0,1,2,3, \ldots \) ортогональны на отрезке \(\left[ {-1,1} \right]:\) \[ \int\limits_{ - 1}^1 {{P_m}\left( x \right){P_n}\left( x \right)dx} = \begin{cases} 0, & m \ne n \\ \frac{2}{{2n + 1}}, & m = n \end{cases}. \] Полиномы Чебышева \({T_n}\left( x \right) = \cos \left( {n\arccos x} \right)\) первого рода ортогональны на отрезке \(\left[ {-1,1} \right]\) с весовой функцией \(\large\frac{1}{{\sqrt {1 - {x^2}} }}\normalsize :\) \[ \int\limits_{ - 1}^1 {\frac{{{T_m}\left( x \right){T_n}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} = \begin{cases} 0, & m \ne n \\ \pi, & m = n = 0 \\ \frac{\pi }{2}, & m = n \ne 0 \end{cases}. \]

   Пример 1

Показать, что множество функций \[1,\cos x,\sin x,\cos 2x,\sin 2x, \ldots ,\cos mx,\sin mx, \ldots \] ортогонально на отрезке \(\left[ { - \pi ,\pi } \right].\) Вычислим следующие интегралы: \[ {{I_1} = \int\limits_{ - \pi }^\pi {\sin mx\sin nxdx} ,}\;\; {{I_2} = \int\limits_{ - \pi }^\pi {\cos mx\cos nxdx} ,}\;\; {{I_3} = \int\limits_{ - \pi }^\pi {\sin mx\cos nxdx} .} \] Первый интеграл равен \[ {{I_1} = \int\limits_{ - \pi }^\pi {\sin mx\sin nxdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\cos \left( {mx - nx} \right) - \cos \left( {mx + nx} \right)} \right]dx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left[ {\cos \left( {m - n} \right)x - \cos \left( {m + n} \right)x} \right]dx} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{\sin \left( {m - n} \right)x}}{{m - n}} - \frac{{\sin \left( {m + n} \right)x}}{{m + n}}} \right)} \right|_{ - \pi }^\pi } \right].} \] Если \(m \ne n,\) то \[ {{I_1} = \frac{1}{2}\left[ {\frac{{\sin \left( {m - n} \right)\pi - \sin \left( {\left( {m - n} \right)\left( { - \pi } \right)} \right)}}{{m - n}}} \right. } - {\left. {\frac{{\sin \left( {m + n} \right)\pi - \sin \left( {\left( {m + n} \right)\left( { - \pi } \right)} \right)}}{{m + n}}} \right] } = {\frac{{\sin \left( {m - n} \right)\pi }}{{m - n}} - \frac{{\sin \left( {m + n} \right)\pi }}{{m + n}} = 0.} \] В случае \(m = n\) получаем \[ {{I_1} = \int\limits_{ - \pi }^\pi {{{\sin }^2}xdx} } = {\frac{1}{2}\int\limits_{ - \pi }^\pi {\left( {1 - \cos 2nx} \right)dx} } = {\frac{1}{2}\left[ {\left. {\left( {x - \frac{{\sin 2nx}}{{2n}}} \right)} \right|_{ - \pi }^\pi } \right] } = {\frac{1}{2}\left[ {\pi - \frac{{\sin 2n\pi }}{{2n}} - \left( { - \pi } \right) - \frac{{\sin \left( { - 2n\pi } \right)}}{{2n}}} \right] } = {\pi .} \] Таким образом, \[ {I_1} = \int\limits_{ - \pi }^\pi {\sin mx\sin nxdx} = \begin{cases} 0, & m \ne n \\ \pi, & m = n \end{cases}. \] Аналогично находим, что \[ {I_2} = \int\limits_{ - \pi }^\pi {\cos mx\cos nxdx} = \begin{cases} 0, & m \ne n \\ \pi, & m = n \end{cases}, \] \[ {I_3} = \int\limits_{ - \pi }^\pi {\sin mx\cos nxdx} = \begin{cases} 0, & m \ne n \\ \pi, & m = n \end{cases}. \] Это значит, что последовательность функций \[1,\cos x,\sin x,\cos 2x,\sin 2x, \ldots ,\cos mx,\sin mx, \ldots \] образует ортогональную систему на интервале \(\left[ { - \pi ,\pi } \right].\)

   Пример 2

Найти разложение функции \(f\left( x \right) = A{x^2} + Bx + C\) в ряд Фурье-Эрмита. Воспользуемся явными выражениями для полиномов Эрмита: \[{H_0}\left( x \right) = 1,\;\;{H_1}\left( x \right) = 2x,\;\;{H_2}\left( x \right) = 4{x^2} - 2.\] Применяя метод неопределенных коэффициентов, запишем равенство \[ {A{x^2} + Bx + C } = {{c_0}{H_0}\left( x \right) + {c_1}{H_1}\left( x \right) + {c_2}{H_2}\left( x \right).} \] Подставляя многочлены Эрмита и приравнивая коэффициенты при одинаковых степенях \(x,\) получаем \[ {A{x^2} + Bx + C = {c_0} \cdot 1 + {c_1} \cdot 2x + {c_2} \cdot \left( {4{x^2} - 2} \right),}\;\; {\Rightarrow A{x^2} + Bx + C = {c_0} + 2{c_1}x + 4{c_2}{x^2} - 2{c_2},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {4{c^2} = A}\\ {2{c_1} = B}\\ {{c_0} - 2{c_2} = C} \end{array}} \right.,}\;\; {\Rightarrow {c_0} = C + \frac{A}{2},\;\;{c_1} = \frac{B}{2},\;\;{c_2} = \frac{A}{4}.} \] Следовательно разложение заданной функции в ряд Фурье-Эрмита описывается выражением \[ {f\left( x \right) = A{x^2} + Bx + C } = {\left( {C + \frac{A}{2}} \right){H_0}\left( x \right) + \frac{B}{2}{H_1}\left( x \right) + \frac{A}{4}{H_2}\left( x \right).} \]

   Пример 3

Найти разложение степенной функции \(f\left( x \right) = {x^p},\;p \ge 1\) в ряд Фурье-Лагерра. Данное разложение описывается общей формулой \[f\left( x \right) = \sum\limits_{n = 0}^\infty {{c_n}{L_n}\left( x \right)} .\] Вычислим коэффициенты \({{c_n}}.\) \[ {{c_0} = \int\limits_0^\infty {f\left( x \right){e^{ - x}}dx} } = {\int\limits_0^\infty {{x^p}{e^{ - x}}dx} } = {\Gamma \left( {p + 1} \right) = p!,} \] где \(\Gamma\)− гамма-функция.

Для \(n \ge 1\) получаем: \[ {{c_n} = \frac{1}{{n!}}\int\limits_0^\infty {{x^p}\frac{{{d^n}\left( {{x^n}{e^{ - x}}} \right)}}{{d{x^n}}}dx} } = {\frac{1}{{n!}}\left[ {\left. {\left( {{x^p}\frac{{{d^{n - 1}}\left( {{x^n}{e^{ - x}}} \right)}}{{d{x^{n - 1}}}}} \right)} \right|_0^\infty - \int\limits_0^\infty {p{x^{p - 1}}\frac{{{d^{n - 1}}\left( {{x^n}{e^{ - x}}} \right)}}{{d{x^{n - 1}}}}dx} } \right].} \] Продолжая интегрирование по частям, находим что \[ {{c_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{n!}}p\left( {p - 1} \right)\left( {p - 2} \right) \cdots \left( {p - n + 1} \right)\int\limits_0^\infty {{x^p}{e^{ - x}}dx} } = {\frac{{{{\left( { - 1} \right)}^n}}}{{n!}} \cdot \frac{{p!}}{{\left( {p - n} \right)!}} \cdot \Gamma \left( {p + 1} \right) } = {\frac{{{{\left( { - 1} \right)}^n}{{\left( {p!} \right)}^2}}}{{n!\left( {p - n} \right)!}},}\;\; {\text{если}\;\;1 \le n \le p.} \] Если же \(n > p,\) то \({c_n} = 0.\)

Следовательно, разложение степенной функции \(f\left( x \right) = {x^p}\) в ряд Фурье-Лагерра имеет вид: \[ {f\left( x \right) = {x^p} } = {p! + \sum\limits_{n = 1}^p {\frac{{{{\left( { - 1} \right)}^n}{{\left( {p!} \right)}^2}}}{{n!\left( {p - n} \right)!}}{L_n}\left( x \right)} .} \] Поскольку \({L_0}\left( x \right) = 1,\) то решение можно записать в более компактной форме: \[ {f\left( x \right) = {x^p} } = {\sum\limits_{n = 0}^p {\frac{{{{\left( { - 1} \right)}^n}{{\left( {p!} \right)}^2}}}{{n!\left( {p - n} \right)!}}{L_n}\left( x \right)} .} \] Проверим ответ, например, для \(p = 2.\) Тогда \[ {{x^2} = \sum\limits_{n = 0}^2 {\frac{{{{\left( { - 1} \right)}^n}{{\left( {2!} \right)}^2}}}{{n!\left( {2 - n} \right)!}}{L_n}\left( x \right)} } = {2{L_0}\left( x \right) - 4{L_1}\left( x \right) + 2{L_2}\left( x \right).} \] Подставляя полиномы Лагерра \[ {{L_0}\left( x \right) = 1,\;\;{L_1}\left( x \right) = 1 - x,}\;\; {{L_2}\left( x \right) = 1 - 2x + \frac{{{x^2}}}{2} } \] в приведенную выше формулу, получаем тождество \[ {{x^2} } = {2 \cdot 1 - 4\left( {1 - x} \right) + 2\left( {1 - 2x + \frac{{{x^2}}}{2}} \right) } {\equiv {x^2}.} \]

   Пример 4

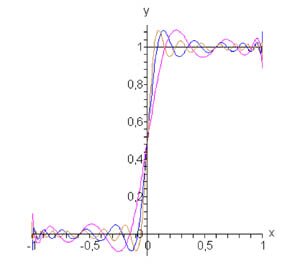
Найти разложение в ряд Фурье-Лежандра ступенчатой функции \[ f\left( x \right) = \begin{cases} 0, & -1 \lt x \lt 0 \\ 1, & 0 \lt x \lt 1 \end{cases}. \] Разложение в ряд записывается в виде \[f\left( x \right) = \sum\limits_{n = 0}^\infty {{c_n}{P_n}\left( x \right)} .\] Подставляя явные выражения полиномов Лежандра, получаем \[ {f\left( x \right) = \frac{{2n + 1}}{2}\int\limits_{ - 1}^1 {f\left( x \right){P_n}\left( x \right)dx} } = {\frac{{2n + 1}}{2}\int\limits_0^1 {{P_n}\left( x \right)dx} } = {\frac{{2n + 1}}{2}\int\limits_0^1 {\frac{1}{{{2^n}n!}}\frac{{{d^n}{{\left( {{x^2} - 1} \right)}^n}}}{{d{x^n}}}dx} } = {\frac{{2n + 1}}{{{2^{n + 1}}n!}}\left[ {\left. {\left( {\frac{{{d^{n - 1}}{{\left( {{x^2} - 1} \right)}^n}}}{{d{x^{n - 1}}}}} \right)} \right|_0^1} \right],}\;\; {n = 1,2,3, \ldots } \] Вычислим коэффициенты \({c_n}.\) Для \(n = 0\) находим, что \({P_0}\left( x \right) = 0.\) Тогда \[ {{c_0} = \frac{1}{2}\int\limits_{ - 1}^1 {f\left( x \right){P_0}\left( x \right)dx} } = {\frac{1}{2}\int\limits_0^1 {dx} = \frac{1}{2}.} \] Вычислим теперь значение производной \({\left. {\left( {\large\frac{{{d^{n - 1}}{{\left( {{x^2} - 1} \right)}^n}}}{{d{x^{n - 1}}}}\normalsize} \right)} \right|_0^1},\) чтобы найти коэффициенты \({c_n}\) при \(n \ge 1.\) Очевидно, что при \(x = 1\) это выражение равно \(0\) при любых \(n \ge 1.\) Чтобы определить значение производной в точке \(x = 0,\) применим биномиальную формулу Ньютона: \[ {\frac{{{d^{n - 1}}{{\left( {{x^2} - 1} \right)}^n}}}{{d{x^{n - 1}}}} } = {\frac{{d{{\left( {\sum\limits_{m = 0}^\infty {C_n^m{{\left( { - 1} \right)}^m}{x^{2n - 2m}}} } \right)}^{n - 1}}}}{{d{x^{n - 1}}}} } = {\sum\limits_{m = 0}^{m \le \frac{{n + 1}}{2}} {\left[ {C_n^m{{\left( { - 1} \right)}^m}\left( {2n - 2m} \right)\left( {2n - 2m - 1} \right)} \right.} } {\cdots \left. {\left( { - 2m + n + 2} \right){x^{n - 2m + 1}}} \right].} \] Отсюда видно, что сумма равна нулю при \(x = 0\) для четных чисел \(n = 2k,\;k = 0,1,2,3, \ldots \) Для нечетных чисел сумма ряда в точке \(x = 0\) будет равна \[ {C_{2k + 1}^{k + 1}{\left( { - 1} \right)^{k + 1}}2k\left( {2k - 1} \right)\left( {2k - 2} \right) \cdots 3 \cdot 2 } = {C_{2k + 1}^{k + 1}{\left( { - 1} \right)^{k + 1}}\left( {2k} \right)!} \] Мы использовали здесь то обстоятельство, что для \(n = 2k + 1\) и \(m = k + 1\) справедливо равенство \({x^{n - 2m + 1}} = {x^{2k + 1 - 2\left( {k + 1} \right) + 1}} = {x^0} = 1\) при \(x \to 0.\) Для других значений \(m\) и \(n\) члены ряда равны нулю. Следовательно, \[{c_{2k}} = 0,\] \[ {{c_{2k + 1}} = \frac{{4k + 3}}{{{2^{2k + 2}}\left( {2k + 1} \right)!}} \cdot \frac{{\left( {2k + 1} \right)!}}{{\left( {k + 1} \right)!k!}}{\left( { - 1} \right)^k}\left( {2k} \right)! } = {\frac{{{{\left( { - 1} \right)}^k}\left( {4k + 3} \right)\left( {2k} \right)!}}{{{2^{2k + 2}}\left( {k + 1} \right)!k!}}.} \] Таким образом, разложение ступенчатой функции в ряд Фурье-Лежандра представляется формулой \[ {f\left( x \right) } = {\frac{1}{2} + \sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}\left( {4k + 3} \right)\left( {2k} \right)!}}{{{2^{2k + 2}}\left( {k + 1} \right)!k!}}{P_{2k + 1}}\left( x \right)} .} \] На рисунке \(1\) показаны аппроксимации ступенчатой функции данным рядом при \(n = 5, 10 \;\text{и}\;15.\)

   Пример 5

Найти разложение функции \(f\left( x \right) = {x^3}\) в ряд Фурье-Чебышева на интервале \(\left[ { - 1,1} \right].\) Исходя из общих представлений, можно записать \[ {{x^3} = \sum\limits_{n = 0}^\infty {{c_n}{T_n}\left( x \right)} } = {{c_0} + \sum\limits_{n = 1}^\infty {{c_n}{T_n}\left( x \right)} .} \] Для вычисления коэффициентов \({{c_n}}\) воспользуемся свойством ортогональности многочленов Чебышева на интервале \(\left[ { - 1,1} \right]\) с весовой функцией \(\large\frac{1}{{\sqrt {1 - {x^2}} }}\normalsize .\)
Умножая обе части последнего равенства на \(\large\frac{1}{{\sqrt {1 - {x^2}} }}\normalsize\) и интегрируя на отрезке \(\left[ { - 1,1} \right],\) получаем \[ {\int\limits_{ - 1}^1 {\frac{{{x^3}dx}}{{\sqrt {1 - {x^2}} }}} } = {\int\limits_{ - 1}^1 {\left( {\sum\limits_{n = 0}^\infty {{c_n}{T_n}\left( x \right)} } \right)\frac{{dx}}{{\sqrt {1 - {x^2}} }}} .} \] Поскольку функция \(f\left( x \right) = {x^3}\) нечетная, и мы интегрируем на симметричном интервале \(\left[ { - 1,1} \right],\) то интеграл в левой части равен \(0:\) \[\int\limits_{ - 1}^1 {\frac{{{x^3}dx}}{{\sqrt {1 - {x^2}} }}} = 0.\] Преобразуем правую часть: \[ {\int\limits_{ - 1}^1 {\left( {\sum\limits_{n = 0}^\infty {{c_n}{T_n}\left( x \right)} } \right)\frac{{dx}}{{\sqrt {1 - {x^2}} }}} } = {\int\limits_{ - 1}^1 {\left( {{c_0} + \sum\limits_{n = 1}^\infty {{c_n}{T_n}\left( x \right)} } \right)\frac{{dx}}{{\sqrt {1 - {x^2}} }}} } = {{c_0}\int\limits_{ - 1}^1 {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} + \sum\limits_{n = 1}^\infty {\left[ {{c_n}\int\limits_{ - 1}^1 {\frac{{{T_n}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} } \right]} .} \] Умножая в последнем интеграле числитель подынтегрального выражения на \({T_0}\left( x \right) = 1,\) видим, что \[\int\limits_{ - 1}^1 {\frac{{{T_n}\left( x \right){T_0}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} = 0\] вследствие ортогональности многочленов Чебышева.

Таким образом, \[{c_0}\int\limits_{ - 1}^1 {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} = 0.\] Вычисляя, находим \[ {\int\limits_{ - 1}^1 {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} } = {\left. {\left( {\arcsin x} \right)} \right|_{ - 1}^1 } = {\arcsin 1 - \arcsin \left( { - 1} \right) } = {\frac{\pi }{2} - \left( { - \frac{\pi }{2}} \right) } = {\pi .} \] Следовательно, \({c_0} = 0.\)

Аналогично можно определить коэффициенты \({c_n}.\)
Умножим выражение \({x^3} = \sum\limits_{n = 0}^\infty {{c_n}{T_n}\left( x \right)} \) на \(\large\frac{{{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}\normalsize,\;m = 1,2,3, \ldots \) и проинтегрируем его от \(-1\) до \(1.\) Получаем \[ {{\int\limits_{ - 1}^1 {\frac{{{x^3}{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} } = {\int\limits_{ - 1}^1 {\left( {\sum\limits_{n - 0}^\infty {{c_n}{T_n}\left( x \right)} } \right)\frac{{{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} ,}}\;\; {{\Rightarrow \int\limits_{ - 1}^1 {\frac{{{x^3}{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} } = {\sum\limits_{n = 0}^\infty {\left[ {{c_n}\int\limits_{ - 1}^1 {\frac{{{T_n}\left( x \right){T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} } \right]} ,}}\;\; {\Rightarrow \int\limits_{ - 1}^1 {\frac{{{x^3}{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} = \frac{\pi }{2}{c_m}.} \] в силу свойства ортогональности.

Подставим далее явные выражения для \({{T_m}\left( x \right)}\) и сделаем замену переменной: \[ {x = \cos t,\;\; \Rightarrow \arccos x = t,}\;\; {\Rightarrow - \frac{{dx}}{{\sqrt {1 - {x^2}} }} = dt.} \] Пределы интегрирования будут равны Тогда \[ {{c_m} = \frac{2}{\pi }\int\limits_{ - 1}^1 {\frac{{{x^3}{T_m}\left( x \right)}}{{\sqrt {1 - {x^2}} }}dx} } = {\frac{2}{\pi }\int\limits_0^1 {{{\cos }^3}t\cos mtdt} } = {\frac{2}{\pi }\int\limits_0^\pi {\frac{1}{4}\left( {3\cos t + \cos 3t} \right)\cos mtdt} } = {\frac{3}{{2\pi }}\int\limits_0^\pi {\cos t\cos mtdt} + \frac{1}{{2\pi }}\int\limits_0^\pi {\cos 3t\cos mtdt} .} \] Вычислим полученные интегралы отдельно. \[ {\int\limits_0^\pi {\cos t\cos mtdt} } = {\frac{1}{2}\int\limits_0^\pi {\left[ {\cos \left( {t - mt} \right) + \cos \left( {t + mt} \right)} \right]dt} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{\sin \left( {m - 1} \right)t}}{{m - 1}} + \frac{{\sin \left( {m + 1} \right)t}}{{m + 1}}} \right)} \right|_0^\pi } \right] = 0,}\;\; {\text{если}\;\;m \ne 1.} \] Для случая \(m = 1\) имеем \[ {\int\limits_0^\pi {{{\cos }^2}tdt} } = {\frac{1}{2}\int\limits_0^\pi {\left( {1 + \cos 2t} \right)dt} } = {\frac{1}{2}\left[ {\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^\pi } \right] } = {\frac{\pi }{2}.} \] Аналогично вычислим второй интеграл: \[ {\int\limits_0^\pi {\cos 3t\cos mtdt} } = {\frac{1}{2}\int\limits_0^\pi {\left[ {\cos \left( {3t - mt} \right) + \cos \left( {3t + mt} \right)} \right]dt} } = {\frac{1}{2}\left[ {\left. {\left( {\frac{{\sin \left( {m - 3} \right)t}}{{m - 3}} + \frac{{\sin \left( {m + 3} \right)t}}{{m + 3}}} \right)} \right|_0^\pi } \right] = 0,}\;\; {\text{если}\;\;m \ne 3.} \] Если \(m = 3,\) то получаем \[ {\int\limits_0^\pi {{{\cos }^2}3tdt} } = {\frac{1}{2}\int\limits_0^\pi {\left( {1 + \cos 6t} \right)dt} } = {\frac{1}{2}\left[ {\left. {\left( {t + \frac{{\sin 6t}}{6}} \right)} \right|_0^\pi } \right] } = {\frac{\pi }{2}.} \] Итак, видно, что множество функций \(1,\cos t,\cos 2t,\cos 3t, \ldots ,\cos mt, \ldots \) ортогонально на интервале \(\left[ {0,\pi } \right],\) и коэффициенты \({c_m}\) равны \[ {c_m} = \begin{cases} 0, & m \ne 1,3 \\ \frac{3}{4}, & m = 1 \\ \frac{1}{4}, & m = 3 \end{cases}. \] Следовательно, разложение в ряд Фурье-Чебышева функции \(f\left( x \right) = {x^3}\) на интервале \(\left[ { - 1,1} \right]\) имеет вид: \[f\left( x \right) = {x^3} = \frac{3}{4}{T_1}\left( x \right) + \frac{1}{4}{T_3}\left( x \right).\]