Неравенства и промежутки числовой прямой  

Неравенство	Промежуток	Графическое обозначение
\(a \le x \le b\)	\(\left[ {a,b} \right]\)
\(a \lt x \le b\)	\(\left( {a,b} \right]\)
\(a \le x \lt b\)	\(\left[ {a,b} \right)\)
\(a \lt x \lt b\)	\(\left( {a,b} \right)\)
\( - \infty \lt x \le b\) или \(x \le b\)	\(\left( {-\infty,b} \right]\)
\( - \infty \lt x \lt b\)	\(\left( {-\infty,b} \right)\)
\(a \le x \lt \infty\) или \(x \ge a\)	\(\left[ {a,\infty} \right)\)
\(a \lt x \lt \infty\) или \(x \gt a\)	\(\left( {a,\infty} \right)\)

Строгие неравенства
\(a < b\) означает "\(a\) меньше, чем \(b\)",
\(a > b\) означает "\(a\) больше, чем \(b\)".

Нестрогие неравенства
\(a \le b\) означает "\(a\) меньше или равно \(b\)",
\(a \ge b\) означает "\(a\) больше или равно \(b\)".

Если \(a > b\), то \(b < a\).

Если \(a > b\), то \(a - b > 0\) или (эквивалентно) \(b - a < 0\).

Свойство транзитивности
Если \(a > b\) и \(b > c\), то \(a > c\).

Знак неравенства сохраняется, если к обеим частям прибавить одно и то же произвольное число:
Если \(a > b\), то \(a + c > b + c\).

Любое слагаемое можно перенести из одной части неравенства в другую, изменив его знак на противоположный:
Если \(a + b > c\), то \(a > c - b\).

Если \(a > b\) и \(c > d\), то \(a + c > b + d\).

Если \(a > b\) и \(c > d\), то \(a - d > b - c\).

Знак неравенства сохраняется, если обе части умножить на одно и то же положительное число:
Если \(a > b\) и \(m > 0\), то \(ma > mb\).

Знак неравенства сохраняется, если обе части разделить на одно и то же положительное число:
Если \(a > b\) и \(m > 0\), то \(a/m > b/m\).

Знак неравенства меняется на противоположный, если обе части умножить на одно и то же отрицательное число:
Если \(a > b\) и \(m < 0\), то \(ma < mb\).

Знак неравенства меняется на противоположный, если обе части разделить на одно и то же отрицательное число:
Если \(a > b\) и \(m < 0\), то \(a/m < b/m\).

Если \(a > b > 0\), то \(1/b > 1/a\).

Умножение неравенств
Если \(a > b > 0\) и \(c > d > 0\), то \(ac > bd\).

Деление неравенств
Если \(a \ge b > 0\) и \(c > d > 0\), то \(a/d > b/c\).

Возведение неравенства в степень при положительном показателе
Если \(a > b > 0\) и \(n > 0\), то \({a^n} > {b^n}\).

Возведение неравенства в степень при отрицательном показателе
Если \(a > b > 0\) и \(n < 0\), то \({a^n} < {b^n}\).

Извлечение корня из неравенства
Если \(a > b > 0\) и \(n > 0\), то \(\sqrt[\large n\normalsize]{a} > \sqrt[\large n\normalsize]{b}\).

\(a + \large\frac{1}{a}\normalsize \ge 2\;\;\left( {a > 0} \right)\) 
Равенство имеет место лишь при \(a = 1\).

Неравенство Коши (соотношение между средним арифметическим и средним геометрическим)
\(\sqrt {ab} \le \left( {a + b} \right)/2,\text { где }a > 0,b > 0\).
Равенство выполняется лишь при \(a = b\).

Неравенство Коши (случай нескольких переменных)
\(\sqrt[n]{{{a_1}{a_2} \cdots {a_n}}} \le \large\frac{{{a_1} + {a_2} + \ldots + {a_n}}}{n}\normalsize,\text { где }{a_1},{a_2}, \ldots ,{a_n} > 0\).

Линейное неравенство (случай \(a > 0\))
Если \(ax + b > 0\) и \(a > 0\), то \(x > -b/a\).

Линейное неравенство (случай \(a < 0\))
Если \(ax + b > 0\) и \(a < 0\), то \(x < -b/a\).

Квадратное неравенство
\(a{x^2} + bx + c > 0\)

	\(a > 0\)	\(a < 0\)
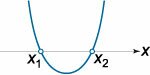
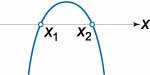
\(D > 0\)	\(x < {x_1}\), \(x > {x_2}\)	\({x_1} < x < {x_2}\)
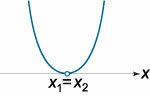
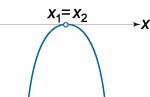
\(D = 0\)	\(x < {x_1}\), \(x > {x_1}\)	\(x \in \emptyset\)
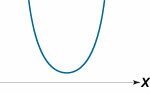
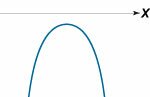
\(D < 0\)	\( - \infty < x < \infty \)	\(x \in \emptyset\)

\(\left| {a + b} \right| \le \left| a \right| + \left| b \right|\) 

Если \(\left| x \right| < a\), то \(-a < x < a\), где \(a > 0\).

Если \(\left| x \right| > a\), то \(x < -a\) и \(x > a\), где \(a > 0\).

Если \({x^2} < a\), то \(\left| x \right| < \sqrt a \), где \(a > 0\).

Если \({x^2} > a\), то \(\left| x \right| > \sqrt a \), где \(a > 0\).

\(\large\frac{{f\left( x \right)}}{{g\left( x \right)}}\normalsize > 0,\;\; \Leftrightarrow \;f\left( x \right)g\left( x \right) > 0\;\; \Leftrightarrow \;\begin{cases} {f\left( x \right)} > 0 \\ {g\left( x \right)} > 0 \end{cases} \;\text { или }\; \begin{cases} {f\left( x \right)} < 0 \\ {g\left( x \right)} < 0 \end{cases}. \) 

\(\large\frac{{f\left( x \right)}}{{g\left( x \right)}}\normalsize < 0,\;\; \Leftrightarrow \;f\left( x \right)g\left( x \right) < 0\;\; \Leftrightarrow \;\begin{cases} {f\left( x \right)} > 0 \\ {g\left( x \right)} < 0 \end{cases} \;\text { или }\; \begin{cases} {f\left( x \right)} < 0 \\ {g\left( x \right)} > 0 \end{cases}. \) 

\(\large\frac{{f\left( x \right)}}{{g\left( x \right)}}\normalsize \ge 0,\;\; \Leftrightarrow \; \begin{cases} {f\left( x \right) g\left( x \right)} \ge 0 \\ {g\left( x \right)} \ne 0 \end{cases} \; \Leftrightarrow \;\begin{cases} {f\left( x \right)} \ge 0 \\ {g\left( x \right)} > 0 \end{cases} \;\text { или }\; \begin{cases} {f\left( x \right)} \le 0 \\ {g\left( x \right)} < 0 \end{cases}. \) 

\(\large\frac{{f\left( x \right)}}{{g\left( x \right)}}\normalsize \le 0,\;\; \Leftrightarrow \; \begin{cases} {f\left( x \right) g\left( x \right)} \le 0 \\ {g\left( x \right)} \ne 0 \end{cases} \; \Leftrightarrow \;\begin{cases} {f\left( x \right)} \le 0 \\ {g\left( x \right)} > 0 \end{cases} \;\text { или }\; \begin{cases} {f\left( x \right)} \ge 0 \\ {g\left( x \right)} < 0 \end{cases}. \)