|
|
|
|
Непрерывность функций
|
|
Определение непрерывности по Гейне
Говорят, что функция действительного переменного \(f\left( x \right)\) является непрерывной в точке \(a \in \mathbb{R}\) (\(\mathbb{R}-\)множество действительных чисел), если для любой последовательности \(\left\{ {{x_n}} \right\}\), такой, что \[\lim\limits_{n \to \infty } {x_n} = a,\] выполняется соотношение \[\lim\limits_{n \to \infty } f\left( {{x_n}} \right) = f\left( a \right).\] На практике удобно использовать следующие \(3\) условия непрерывности функции \(f\left( x \right)\) в точке \(x = a\) (которые должны выполняться одновременно):
- Функция \(f\left( x \right)\) определена в точке \(x = a\);
- Предел \(\lim\limits_{x \to a} f\left( x \right)\) существует;
- Выполняется равенство \(\lim\limits_{x \to a} f\left( x \right) = f\left( a \right)\).
Определение непрерывности по Коши (нотация \(\varepsilon - \delta\))
Рассмотрим функцию \(f\left( x \right)\), которая отображает множество действительных чисел \(\mathbb{R}\) на другое подмножество \(B\) действительных чисел. Говорят, что функция \(f\left( x \right)\) является непрерывной в точке \(a \in \mathbb{R}\), если для любого числа \(\varepsilon > 0\) существует число \(\delta > 0\), такое, что для всех \(x \in \mathbb{R}\), удовлетворяющих соотношению \[\left| {x - a} \right| < \delta ,\] выполняется неравенство \[\left| {f\left( x \right) - f\left( a \right)} \right| < \varepsilon .\]
Определение непрерывности в терминах приращений аргумента и функции
Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке \(x = a\), если справедливо равенство \[\lim\limits_{\Delta x \to 0} \Delta y = \lim\limits_{\Delta x \to 0} \left[ {f\left( {a + \Delta x} \right) - f\left( a \right)} \right] = 0,\] где \(\Delta x = x - a\).
Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.
Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.
Теоремы непрерывности
Теорема 1.
Пусть функция \(f\left( x \right)\) непрерывна в точке \(x = a\) и \(C\) является константой. Тогда функция \(Cf\left( x \right)\) также непрерывна при \(x = a\).
Теорема 2.
Даны две функции \({f\left( x \right)}\) и \({g\left( x \right)}\), непрерывные в точке \(x = a\). Тогда сумма этих функций \({f\left( x \right)} + {g\left( x \right)}\) также непрерывна в точке \(x = a\).
Теорема 3.
Предположим, что две функции \({f\left( x \right)}\) и \({g\left( x \right)}\) непрерывны в точке \(x = a\). Тогда произведение этих функций \({f\left( x \right)} {g\left( x \right)}\) также непрерывно в точке \(x = a\).
Теорема 4.
Даны две функции \({f\left( x \right)}\) и \({g\left( x \right)}\), непрерывные при \(x = a\). Тогда отношение этих функций \(\large\frac{{f\left( x \right)}}{{g\left( x \right)}}\normalsize\) также непрерывно при \(x = a\) при условии, что \({g\left( a \right)} \ne 0\).
Теорема 5.
Предположим, что функция \({f\left( x \right)}\) является дифференцируемой в точке \(x = a\). Тогда функция \({f\left( x \right)}\) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).
Теорема 6 (Теорема о предельном значении).
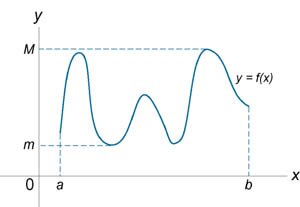
Если функция \({f\left( x \right)}\) непрерывна на закрытом и ограниченном интервале \(\left[ {a,b} \right]\), то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа \(m\) и \(M\), такие, что \[m \le f\left( x \right) \le M\] для всех \(x\) в интервале \(\left[ {a,b} \right]\) (рисунок 1).
Теорема 7 (Теорема о промежуточном значении).
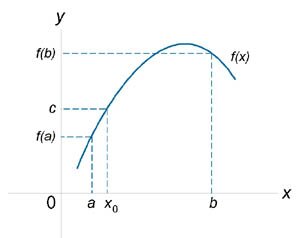
Пусть функция \({f\left( x \right)}\) непрерывна на закрытом и ограниченном интервале \(\left[ {a,b} \right]\). Тогда, если \(c\) − некоторое число, большее \({f\left( a \right)}\) и меньшее \({f\left( b \right)}\), то существует число \({x_0}\), такое, что \[f\left( {{x_0}} \right) = c.\] Данная теорема проиллюстрирована на рисунке 2.
Непрерывность элементарных функций
Все элементарные функции являются непрерывными в любой точке свой области определения.
Функция называется элементарной, если она построена из конечного числа композиций и комбинаций
(с использованием \(4\) действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
- Алгебраические многочлены \(A{x^n} + B{x^{n - 1}} + \ldots + Kx + L;\)
- Рациональные дроби \(\large\frac{{A{x^n} + B{x^{n - 1}} + \ldots + Kx + L}}{{M{x^m} + N{x^{m - 1}} + \ldots + Tx + U}}\normalsize\);
-
Степенные функции \({x^p}\);
-
Показательные функции \({a^x}\);
-
Логарифмические функции \({\log _a}x\);
-
Тригонометрические функции \(\sin x\), \(\cos x\), \(\tan x\), \(\cot x\), \(\sec x\), \(\csc x\);
-
Обратные тригонометрические функции \(\arcsin x\), \(\arccos x\), \(\arctan x\), \(\text{arccot }x\), \(\text{arcsec }x\), \(\text{arccsc }x\);
-
Гиперболические функции \(\sinh x\), \(\cosh x\), \(\tanh x\), \(\coth x\), \(\text{sech }x\), \(\text{csch }x\);
-
Обратные гиперболические функции \(\text{arcsinh }x\), \(\text{arccosh }x\), \(\text{arctanh }x\), \(\text{arccoth }x\), \(\text{arcsech }x\), \(\text{arccsch }x\).
|
|
Пример 1
|
|
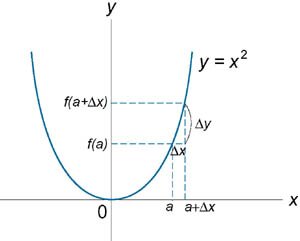
Используя определение непрерывности в терминах приращений, доказать, что функция \(f\left( x \right) = {x^2}\) непрерывна в произвольной точке \(x= a\).
Решение.
Условие непрерывности по Гейне можно записать в виде \[ {\lim\limits_{\Delta x \to 0} f\left( {a + \Delta x} \right) = f\left( a \right)\;\;} {\text{или}\;\;\lim\limits_{\Delta x \to 0} \left[ {f\left( {a + \Delta x} \right) - f\left( a \right)} \right] } = {\lim\limits_{\Delta x \to 0} \Delta y = 0,} \] где \(\Delta x\) и \(\Delta y\) − малые приращения, показанные на рисунке \(3\). Для заданной функции справедливы следующие соотношения в точке \(x = a\): \[f\left( a \right) = {a^2},\;\;f\left( {a + \Delta x} \right) = {\left( {a + \Delta x} \right)^2}.\] Следовательно, \[\require{cancel} {\Delta y = f\left( {a + \Delta x} \right) - f\left( a \right) } = {{\left( {a + \Delta x} \right)^2} - {a^2} } = {\cancel{a^2} + 2a\Delta x + {\left( {\Delta x} \right)^2} - \cancel{a^2} } = {2a\Delta x + {\left( {\Delta x} \right)^2}.} \] Вычислим предел. \[ {\lim\limits_{\Delta x \to 0} \Delta y = \lim\limits_{\Delta x \to 0} \left( {2a\Delta x + {{\left( {\Delta x} \right)}^2}} \right) } = {\lim\limits_{\Delta x \to 0} \left( {2a\Delta x} \right) + \lim\limits_{\Delta x \to 0} {\left( {\Delta x} \right)^2} } = {2a\lim\limits_{\Delta x \to 0} \Delta x + \lim\limits_{\Delta x \to 0} \Delta x \cdot \lim\limits_{\Delta x \to 0} \Delta x } = {2a \cdot 0 + 0 \cdot 0 = 0.} \] Таким образом, функция является непрерывной в произвольной точке \(x = a\).
|
|
Пример 2
|
|
Используя определение непрерывности в терминах приращений, показать, что функция \(f\left( x \right) = \sec x\) непрерывна в любой точке своей области определения.
Решение.
Функция секанс \(f\left( x \right) = \sec x = \large\frac{1}{{\cos x}}\normalsize\) определена для всех действительных \(x\), за исключением точек \[x = \frac{\pi }{2} + k\pi ,\;\;k = 0, \pm 1, \pm 2, \ldots ,\] где косинус равен нулю. Обозначим дифференциал независимой переменной \(x\) через \(\Delta x\). Вычислим соответствующий дифференциал функции \(\Delta y\). \[ {\Delta y = \sec \left( {x + \Delta x} \right) - \sec x } = {\frac{1}{{\cos \left( {x + \Delta x} \right)}} - \frac{1}{{\cos x}} } = {\frac{{\cos - \cos \left( {x + \Delta x} \right)}}{{\cos \left( {x + \Delta x} \right)\cos x}} } = {\frac{{ - 2\sin \left( {x + \frac{{\Delta x}}{2}} \right)\sin \left( { - \frac{{\Delta x}}{2}} \right)}}{{\cos \left( {x + \Delta x} \right)\cos x}} } = {\frac{{2\sin \left( {x + \frac{{\Delta x}}{2}} \right)\sin \frac{{\Delta x}}{2}}}{{\cos \left( {x + \Delta x} \right)\cos x}}.} \] Перейдем к пределу при \(\Delta x \to 0\). \[ {\lim\limits_{\Delta x \to 0} \Delta y = \lim\limits_{\Delta x \to 0} \frac{{2\sin \left( {x + \frac{{\Delta x}}{2}} \right)\sin \frac{{\Delta x}}{2}}}{{\cos \left( {x + \Delta x} \right)\cos x}} } = {\lim\limits_{\Delta x \to 0} \frac{{2\sin \left( {x + \frac{{\Delta x}}{2}} \right)}}{{\cos \left( {x + \Delta x} \right)\cos x}} \cdot \lim\limits_{\Delta x \to 0} \sin \frac{{\Delta x}}{2} } = {\frac{{2\sin x}}{{{{\cos }^2}x}} \cdot 0 = 0.} \] Полученный результат справедлив для всех \(x\) за исключением нулей косинуса: \[x = \frac{\pi }{2} + k\pi ,\;\;k = 0, \pm 1, \pm 2, \ldots\] Следовательно, область непрерывности и область определения функции \(f\left( x \right) = \sec x\) совпадают.
|
|
Пример 3
|
|
Используя определение непрерывности по Коши, доказать, что \(\lim\limits_{x \to 4} \sqrt x = 2\).
Решение.
Пусть \(\varepsilon > 0\). Мы должны найти некоторое число \(\delta > 0\), такое, что для всех \(x\), удовлетворяющих неравенству \[\left| {x - 4} \right| < \delta ,\] будет выполнено соотношение \[\left| {f\left( x \right) - f\left( 4 \right)} \right| < \varepsilon \;\;\text{или}\;\;\left| {\sqrt x - 2} \right| < \varepsilon .\] Последнее неравенство можно записать в виде \[ {- \varepsilon < \sqrt x - 2 < \varepsilon ,}\;\; {\Rightarrow \;\;2 - \varepsilon < \sqrt x < \varepsilon + 2,}\;\; {\Rightarrow {\left( {2 - \varepsilon } \right)^2} < x < {\left( {\varepsilon + 2} \right)^2},}\;\; {\Rightarrow {\varepsilon ^2} - 4\varepsilon + 4 < x < {\varepsilon ^2} + 4\varepsilon + 4.} \] Следовательно, \[{\varepsilon ^2} - 4\varepsilon < x - 4 < {\varepsilon ^2} + 4\varepsilon .\] Заметим, что наша функция принимает лишь неотрицательные значения. Поэтому в заданной точке для \(\varepsilon\)-окрестности должно выполняться условие \(\varepsilon \le 2\). В этом случае левая часть \({\varepsilon ^2} - 4\varepsilon\) неравенства будет отрицательной. Отсюда следует соотношение \[ {{\varepsilon ^2} - 4\varepsilon < x - 4 < 4\varepsilon - {\varepsilon ^2}}\;\; {\text{или}\;\;\left| {x - 4} \right| < 4\varepsilon - {\varepsilon ^2}.} \] Таким образом, если мы выберем \(\delta \le {\varepsilon ^2} - 4\varepsilon\), то для всех \(x\), удовлетворяющих неравенству \(\left| {x - 4} \right| < \delta\), получим \(\left| {f\left( x \right)} - 2 \right| < \varepsilon\). Например, если \(\varepsilon = 0.1\), то величина \(\delta\) должна удовлетворять условию \(\delta \le {\varepsilon ^2} - 4\varepsilon = 0.4 - 0.01 = 0.39.\,\) По определению Коши это означает, что \[\lim\limits_{x \to 4} \sqrt x = 2.\]
|
|
Пример 4
|
|
Показать, что кубическое уравнение \(2{x^3} - 3{x^2} - 15 = 0\) имеет решение в интервале \(\left( {2,3} \right)\).
Решение.
Пусть \(f\left( x \right) = 2{x^3} - 3{x^2} - 15\). Вычислим значения функции при \(x = 2\) и \(x = 3\). \[ {f\left( 2 \right) = 2 \cdot {2^3} - 3 \cdot {2^2} - 15 = - 11,}\;\;\; {f\left( 3 \right) = 2 \cdot {3^3} - 3 \cdot {3^2} - 15 = 12.} \] Мы получили, что \(f\left( 2 \right) < 0\) и \(f\left( 3 \right) > 0\), или \[f\left( 2 \right) < 0 < f\left( 3 \right).\] По теореме о промежуточном значении это означает, что в интервале \(\left( {2,3} \right)\) существует такое число \(c\), что \(f\left( c \right) = 0\). Таким образом, данное уравнение имеет решение в интервале \(\left( {2,3} \right)\).
|
|
Пример 5
|
|
Показать, что уравнение \({x^{1000}} + 1000x - 1 = 0\) имеет, по крайней мере, один корень.
Решение.
Поскольку функция \(f\left( x \right) = {x^{1000}} + 1000x - 1\) является полиномом, то она непрерывна. Заметим, что \[ {f\left( 0 \right) = {0^{1000}} + 1000 \cdot 0 - 1 = - 1,}\;\;\; {f\left( 1 \right) = {1^{1000}} + 1000 \cdot 1 - 1 = 1000.} \] Поэтому \(f\left( 0 \right) < 0 < f\left( 1 \right)\). По теореме о промежуточном значении можно сделать вывод, что в интервале \(\left( {0,1} \right)\) существует число \(c\), такое, что \(f\left( c \right) = 0\). Таким образом, уравнение имеет корень в интервале \(\left( {0,1} \right)\).
|
|
Пример 6
|
|
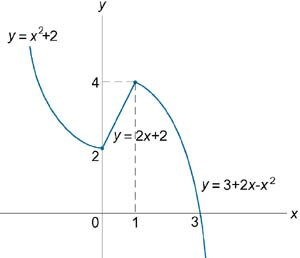
Задана функция \[ f\left(x \right) = \begin{cases} x^2 + 2, & \text{если }\;\;x < 0 \\ ax + b, & \text{если }\;\;0 \le x \lt 1 \\ 3 + 2x - {x^2}, & \text{если }\;\;x \ge 1 \end{cases} .\] Определить коэффициенты \(a\) и \(b\), при которых функция \(f\left(x \right)\) является всюду непрерывной.
Решение.
Найдем левосторонний предел функции в точке \(x = 0\). \[\lim\limits_{x \to 0 - 0} f\left( x \right) = \lim\limits_{x \to 0 - 0} \left( {{x^2} + 2} \right) = 2.\] Следовательно, значение \(ax + b\) в точке \(x = 0\) должно быть равно \(2\). \[ {ax + b = 2,}\;\; {\Rightarrow a \cdot 0 + b = 2,}\;\; {\Rightarrow b = 2.} \] Аналогично, находим правосторонний предел при \(x = 1\). \[ {\lim\limits_{x \to 1 + 0} f\left( x \right) } = {\lim\limits_{x \to 1 + 0} \left( {3 + 2x - {x^2}} \right) } = {3 + 2 - 1 = 4.} \] Как видно, значение \(ax + 2\) в точке \(x = 1\) должно быть равно \(4\). \[ {ax + 2 = 4,}\;\; {\Rightarrow a \cdot 1 + 2 = 4,}\;\; {\Rightarrow a = 2.} \] При данных значениях \(a\) и \(b\) функция \(f\left(x \right)\) будет непрерывной. График функции схематически показан выше на рисунке \(4\).
|
|
Пример 7
|
|
Если функция \[ f\left(x \right) = \begin{cases} \cos \left( {2\pi x- a} \right), &x < -1 \\ x^3 + 1, &x \ge -1 \end{cases} ,\] непрерывна, то чему равно \(a\)?
Решение.
Вычислим левосторонние и правосторонние пределы функции при \(x = -1\). \[ {\lim\limits_{x \to - 1 - 0} f\left( x \right) } = {\lim\limits_{x \to - 1 - 0} \cos \left( {2\pi x - a} \right) } = {\cos \left( { - 2\pi - a} \right) = \cos a,} \] \[ {\lim\limits_{x \to - 1 + 0} f\left( x \right) } = {\lim\limits_{x \to - 1 + 0} \left( {{x^3} + 1} \right) } = {{\left( { - 1} \right)^3} + 1 = 0.} \] Функция будет непрерывной в точке \(x = -1\), если \[ {\lim\limits_{x \to - 1 - 0} f\left( x \right) = \lim\limits_{x \to - 1 + 0} f\left( x \right)}\;\; {\text{или}\;\;\cos a = 0.} \] Следовательно, \[a = \frac{\pi }{2} + \pi n,\;\;n \in \mathbb{Z}.\]
|
|
|
|