Монотонность функций

Пусть \(y = f\left( x \right)\) является дифференцируемой функцией на интервале \(\left( {a,b} \right).\) Функция называется возрастающей (или неубывающей) на данном интервале, если для любых точек \({x_1},{x_2} \in \left( {a,b} \right),\) таких, что \({x_1} < {x_2},\) выполняется неравенство \(f\left( {{x_1}} \right) \le f\left( {{x_2}} \right).\)

Если данное неравенство является строгим, т.е. \(f\left( {{x_1}} \right) \lt f\left( {{x_2}} \right),\) то говорят, что функция \(y = f\left( x \right)\) является строго возрастающей на интервале \(\left( {a,b} \right).\)

Аналогично определяются убывающая (или невозрастающая) и строго убывающая функции.

Введенные понятия можно сформулировать в более компактной форме. Функция \(y = f\left( x \right)\) называется

• возрастающей (неубывающей) на интервале \(\left( {a,b} \right),\) если \[ {\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \le f\left( {{x_2}} \right);} \]
• строго возрастающей на интервале \(\left( {a,b} \right),\) если \[ {\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \lt f\left( {{x_2}} \right);} \]
• убывающей (невозрастающей) на интервале \(\left( {a,b} \right),\) если \[ {\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \ge f\left( {{x_2}} \right);} \]
• строго убывающей на интервале \(\left( {a,b} \right),\) если \[ {\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \gt f\left( {{x_2}} \right).} \]

Ясно, что неубывающая функция может содержать участки строгого возрастания и интервалы, где функция является постоянной. Схематически это иллюстрируется на рисунках \(1-4\). Если функция \(f\left( x \right)\) дифференцируема на интервале \(\left( {a,b} \right)\) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Понятия возрастания и убывания функции можно определить также и для отдельной точки \({x_0}.\) В этом случае рассматривается малая \(\delta\)-окрестность \(\left( {{x_0} - \delta ,{x_0} + \delta } \right)\) этой точки. Функция \(y = f\left( x \right)\) является строго возрастающей в точке \({x_0},\) если существует число \(\delta > 0,\) такое, что \[\forall\;x \in \left( {{x_0} - \delta ,{x_0}} \right) \Rightarrow f\left( x \right) < f\left( {{x_0}} \right);\] \[\forall\;x \in \left( {{x_0}, {x_0} + \delta} \right) \Rightarrow f\left( x \right) > f\left( {{x_0}} \right).\] Аналогичным образом определяется строгое убывание функции \(y = f\left( x \right)\) в точке \({x_0}.\) Снова рассмотрим функцию \(y = f\left( x \right),\) считая ее дифференцируемой на некотором интервале \(\left( {a,b} \right).\) Возрастание или убывание функции на интервале определяется по знаку первой производной функции.

Теорема 1.
Для того, чтобы функция \(y = f\left( x \right)\) была возрастающей на интервале \(\left( {a,b} \right),\) необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале: \[f'\left( x \right) \ge 0\;\forall\;x \in \left( {a,b} \right).\] Аналогичный критерий действует для случая функции, убывающей на интервале \(\left( {a,b} \right):\) \[f'\left( x \right) \le 0\;\forall\;x \in \left( {a,b} \right).\] Докажем обе части теоремы (необходимость и достаточность) для случая возрастающей функции.

Необходимое условие.
Рассмотрим произвольную точку \({x_0} \in \left( {a,b} \right).\) Если функция \(y = f\left( x \right)\) возрастает на \(\left( {a,b} \right),\) то по определению можно записать, что \[\forall\;x \in \left( {a,b} \right):x > {x_0} \Rightarrow f\left( x \right) > f\left( {{x_0}} \right);\] \[\forall\;x \in \left( {a,b} \right):x < {x_0} \Rightarrow f\left( x \right) < f\left( {{x_0}} \right).\] Видно, что в обоих случаях выполняется неравенство \[ {\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \ge 0,}\;\; {\text{где}\;\;x \ne {x_0}.} \] В пределе при \(x \to {x_0}\) левая часть неравенства равна производной функции в точке \({x_0},\) т.е. по свойству сохранения знака предела: \[ {\lim\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} } = {f'\left( {{x_0}} \right) \ge 0.} \] Это соотношение справедливо для любых \({x_0} \in \left( {a,b} \right).\)

Рассмотрим достаточное условие, т.е. обратное утверждение.
Пусть производная \(f'\left( x \right)\) функции \(y = f\left( x \right)\) неотрицательна на интервале \(\left( {a,b} \right):\) \[f'\left( {{x_0}} \right) \ge 0\;\forall\; x \in \left( {a,b} \right).\] Если \({x_1}\) и \({x_2}\) − две произвольные точки данного интервала, такие, что \({x_1}< {x_2},\) то по теореме Лагранжа можно записать: \[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = f'\left( c \right)\left( {{x_2} - {x_1}} \right),\] где \(c \in \left[ {{x_1},{x_2}} \right],\;\; \Rightarrow c \in \left( {a,b} \right).\)

Поскольку \(f'\left( c \right) \ge 0,\) то правая часть равенства неотрицательна. Следовательно, \[f\left( {{x_2}} \right) \ge f\left( {{x_1}} \right).\] т.е. функция \(y = f\left( x \right)\) является возрастающей на интервале \(\left( {a,b} \right).\)

Рассмотрим теперь случаи строгого возрастания и строгого убывания функции. Здесь существует похожая теорема, описывающая необходимые и достаточные условия. Опуская доказательство, сформулируем ее для случая строго возрастающей функции.

Теорема 2.
Для того, чтобы дифференцируемая на интервале \(\left( {a,b} \right)\) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия:

1. \(f'\left( x \right) \ge 0\;\forall\;x \in \left( {a,b} \right);\)

2. Производная \(f'\left( x \right)\) тождественно не равна нулю ни в каком промежутке \(\left[ {{x_1},{x_2}} \right] \in \left( {a,b} \right).\)

Условие \(1\) содержится в теореме \(1\) и является признаком неубывающей функции. Дополнительное условие \(2\) требуется для того, чтобы исключить участки постоянства функции, в которых производная функции \(f\left( x \right)\) тождественно равна нулю.

На практике (при нахождении интервалов монотонности) обычно используется достаточное условие строгого возрастания или строгого убывания функции. Из теоремы \(2\) следует такая формулировка достаточного признака:

Если для всех \(x \in \left( {a,b} \right)\) выполняется условие \(f'\left( x \right) > 0\) всюду в интервале \(\left( {a,b} \right),\) кроме возможно лишь некоторых отдельных точек, в которых \(f'\left( x \right) = 0,\) то функция \(f\left( x \right)\) является строго возрастающей.

Соответственно, условие \(f'\left( x \right) < 0\) определяет строго убывающую функцию.

Число точек, в которых \(f'\left( x \right) = 0,\) является, как правило, конечным. Согласно теореме \(2\), они не могут плотно заполнять какой-либо промежуток в интервале \(\left( {a,b} \right).\)

Приведем также признак строгого возрастания (убывания) функции в точке:

Теорема 3.
Пусть \({x_0} \in \left( {a,b} \right).\)

• Если \(f'\left( {{x_0}} \right) > 0\), то функция \(f\left( x \right)\) строго возрастает в точке \({x_0}\);

• Если \(f'\left( {{x_0}} \right) < 0\), то функция \(f\left( x \right)\) строго убывает в точке \({x_0}\).

Возрастающие и убывающие функции обладают определенными алгебраическими свойствами, которые могут оказаться полезными при исследовании функций. Перечислим некоторые из них:

1. Если функции \(f\) и \(g\) возрастают (убывают) на интервале \(\left( {a,b} \right),\) то сумма функций \(f + g\) также возрастает (убывает) на этом интервале.

2. Если функция \(f\) возрастает (убывает) на интервале \(\left( {a,b} \right),\) то противоположная функция \(-f\) убывает (возрастает) на этом интервале.

3. Если функция \(f\) возрастает (убывает) на интервале \(\left( {a,b} \right),\) то обратная функция \(\large\frac{1}{f}\normalsize\) убывает (возрастает) на этом интервале.

4. Если функции \(f\) и \(g\) возрастают (убывают) на интервале \(\left( {a,b} \right)\) и, кроме того, \(f \ge 0\), \(g \ge 0\), то произведение функций \(fg\) также возрастает (убывает) на этом интервале.

5. Если функция \(g\) возрастает (убывает) на интервале \(\left( {a,b} \right),\) а функция \(f\) возрастает (убывает) на интервале \(\left( {c,d} \right),\) где \(g:\left( {a,b} \right) \to \left( {c,d} \right),\) то композиция функций \(f \circ g\) (т.е. сложная функция \(y = f\left( {g\left( x \right)} \right)\) также возрастает (убывает) на интервале \(\left( {a,b} \right).\)

   Пример 1

Используя определение монотонности, доказать, что функция \(f\left( x \right) = {x^2} + 1\) строго возрастает при \(x \ge 0.\) Возьмем две произвольные точки \({x_1}\) и \({x_2},\) такие что \[0 \le {x_1} \lt {x_2}.\] Рассмотрим разность значений функции в этих точках: \[ {f\left( {{x_2}} \right) - f\left( {{x_1}} \right) } = {\left( {x_2^2 + 1} \right) - \left( {x_1^2 + 1} \right) } = {x_2^2 - x_1^2 } = {\left( {{x_2} - {x_1}} \right)\left( {{x_2} + {x_1}} \right).} \] В последнем выражении, очевидно, что \({{x_2} - {x_1}} > 0\) и \({{x_2} + {x_1}} > 0\) (поскольку по условию рассматриваются неотрицательные значения \(x\)). В результате получаем: \[ {\left( {{x_2} - {x_1}} \right)\left( {{x_2} + {x_1}} \right) > 0,}\;\; {\Rightarrow f\left( {{x_2}} \right) - f\left( {{x_1}} \right) > 0.} \] Это означает по определению, что функция \(f\left( x \right) = {x^2} + 1\) является строго возрастающей на заданном интервале.

   Пример 2

Используя определение монотонности, доказать, что кубическая функция \(f\left( x \right) = {x^3}\) строго возрастает при всех \(x \in \mathbb{R}.\) Выберем две произвольные точки \({{x_1}}\) и \({{x_2}},\) такие что \({x_1} < {x_2}.\) Рассмотрим разность: \[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = x_2^3 - x_1^3.\] Раскладывая ее по формуле разности кубов, получаем: \[ {x_2^3 - x_1^3 } = {\left( {{x_2} - {x_1}} \right)\left( {x_2^2 + {x_1}{x_2} + x_1^2} \right).} \] Во второй скобке можно выделить полный квадрат: \[ {x_2^2 + {x_1}{x_2} + x_1^2 } = {x_1^2 + 2 \cdot {x_1} \cdot \frac{{{x_2}}}{2} + \frac{{x_2^2}}{4} + \frac{{3x_2^2}}{4} } = {{\left( {{x_1} + \frac{{{x_2}}}{2}} \right)^2} + \frac{{3x_2^2}}{4} > 0.} \] Отсюда видно, что квадратичное выражение всегда положительно (оно равно нулю лишь при \({x_1} = {x_2} = 0,\) что противоречит условию \({x_1} < {x_2}.\))

Таким образом, \(f\left( {{x_2}} \right) - f\left( {{x_1}} \right) > 0,\) если \({x_2} - {x_1} > 0,\) т.е. функция \(f\left( x \right) = {x^3}\) является строго возрастающей.

   Пример 3

Используя свойства монотонных функций, доказать, что функция \(f\left( x \right) = {x^4} + 3{x^2}\) строго возрастает при \(x \ge 0.\) Данная функция является суммой функций \({x^4}\) и \(3{x^2}.\)

Первую функцию \({x^4}\) можно рассматривать как произведение двух одинаковых функций \({x^2}\). Из примера \(1\) следует, что квадратичная функция \({x^2}\) строго возрастает при \(x \ge 0.\) Следовательно, функция \({x^4}\) также строго возрастает при \(x \ge 0\) на основании свойства \(4\).

Второе слагаемое \(3{x^2}\) представляет собой трехкратную сумму функций \({x^2}\) и, поэтому, также является строго возрастающей (на основании свойства \(1\)).

Итак, исходная функция \(f\left( x \right) = {x^4} + 3{x^2}\) является суммой двух строго возрастающих функций и, следовательно, также строго возрастает при \(x \ge 0.\)

   Пример 4

Используя определение монотонности, доказать, что функция \(f\left( x \right) = \cos x\) является строго убывающей в промежутке \(\left[ {0,\pi } \right].\) Пусть точки \({x_1}\), \({x_2}\) лежат в заданном интервале \(\left[ {0,\pi } \right]\) и выполняется условие \({x_1} < {x_2}.\) Рассмотрим разность: \[f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \cos {x_2} - \cos {x_1}.\] Преобразуем ее по формуле разности косинусов: \[ {\cos {x_2} - \cos {x_1} } = { - 2\sin \frac{{{x_2} + {x_1}}}{2}\sin \frac{{{x_2} - {x_1}}}{2}.} \] Поскольку \({x_1},{x_2} \in \left[ {0,\pi } \right],\) то полусумма ограничена двойным неравенством \[0 < \frac{{{x_2} + {x_1}}}{2} < \pi .\] Аналогично, полуразность (при условии \({x_2} > {x_1}\)) удовлетворяет неравенству \[0 < \frac{{{x_2} - {x_1}}}{2} < \frac{\pi }{2}.\] Для указанных диапазонов углов синус всегда положителен. Поэтому \[ {\cos {x_2} - \cos {x_1} } = { - 2\sin \frac{{{x_2} + {x_1}}}{2}\sin \frac{{{x_2} - {x_1}}}{2} < 0.} \] Таким образом, выполняется следующее соотношение: \[{x_2} > {x_1} \Rightarrow f\left( {{x_2}} \right) < f\left( {{x_1}} \right),\] т.е. функция косинус строго убывает на интервале \(\left[ {0,\pi } \right].\)

   Пример 5

Найти интервалы монотонности функции \(f\left( x \right) = {x^3} - 12x + 5.\) Производная данной функции имеет вид: \[ {f'\left( x \right) = {\left( {{x^3} - 12x + 5} \right)^\prime } } = {3{x^2} - 12 } = {3\left( {{x^2} - 4} \right).} \] Определим промежутки, в которых производная положительна и отрицательна. Решим следующее неравенство: \[ {f'\left( x \right) > 0,}\;\; {\Rightarrow 3\left( {{x^2} - 4} \right) > 0,}\;\; {\Rightarrow {x^2} - 4 > 0,}\;\; {\Rightarrow \left( {x - 2} \right)\left( {x + 2} \right) > 0.} \] Методом интервалов находим, что \[ {f'\left( x \right) > 0}\;\; {\text{при}\;\;x \in \left( { - \infty , - 2} \right) \cup \left( {2,\infty } \right),} \] \[ {f'\left( x \right) < 0}\;\; {\text{при}\;\;x \in \left( { - 2,2} \right).} \] Следовательно, функция \(f\left( x \right) = {x^3} - 12x + 5\) возрастает (в строгом смысле) в интервалах \(\left( { - \infty , - 2} \right)\) и \(\left( {2,\infty } \right)\) и, соответственно, строго убывает в интервале \(\left( { - 2,2} \right).\)

   Пример 6

Найти интервалы монотонности функции \(f\left( x \right) = x + \sin x.\) Данная функция определена и дифференцируема на всей числовой прямой. Рассмотрим неравенство \(f'\left( x \right) > 0:\) \[ {f'\left( x \right) = {\left( {x + \sin x} \right)^\prime } } ={ 1 + \cos x,} \] \[ {f'\left( x \right) > 0,}\;\; {\Rightarrow 1 + \cos x > 0,}\;\; {\Rightarrow \cos x > - 1.} \] Это неравенство выполняется при всех \(x\) кроме тех точек, где \(\cos x = -1,\) то есть \[ {\cos x \ne - 1,}\;\; {\Rightarrow x \ne \pi + 2\pi n,\;n \in \mathbb{Z}.} \] Однако, если рассматривать нестрогое неравенство \(f'\left( x \right) \ge 0,\) то получаем: \[ {f'\left( x \right) \ge 0,}\;\; {\Rightarrow 1 + \cos x \ge 0,}\;\; {\Rightarrow \cos x \ge - 1,}\;\; {\Rightarrow x \in \mathbb{R}.} \] Таким образом, функция \(f\left( x \right) = x + \sin x\) возрастает (не в строгом смысле, т.е. не убывает) при любых \(x \in \mathbb{R}.\)

Для контроля рассмотрим также неравенство \(f'\left( x \right) < 0:\) \[ {f'\left( x \right) < 0,}\;\; {\Rightarrow 1 + \cos x < 0,}\;\; {\Rightarrow \cos x < - 1,}\;\; {\Rightarrow x \in \emptyset .} \] Это неравенство не имеет решений.

   Пример 7

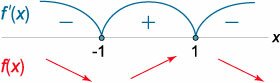
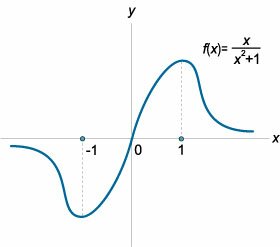
Найти интервалы монотонности функции \[f\left( x \right) = \frac{x}{{{x^2} + 1}}.\] Функция определена и дифференцируема на всем множестве действительных чисел. Вычислим ее производную: \[ {f'\left( x \right) = {\left( {\frac{x}{{{x^2} + 1}}} \right)^\prime } } = {\frac{{x'\left( {{x^2} + 1} \right) - x\left( {{x^2} + 1} \right)'}}{{{{\left( {{x^2} + 1} \right)}^2}}} } = {\frac{{1 \cdot \left( {{x^2} + 1} \right) - x \cdot 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} } = {\frac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}}.} \] Определим интервалы знакопостоянства производной. Приравниваем производную нулю и находим корни уравнения: \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {1 - {x^2} = 0}\\ {{{\left( {{x^2} + 1} \right)}^2} \ne 0} \end{array}} \right.,}\;\; {\Rightarrow 1 - {x^2} = 0,}\;\; {\Rightarrow \left( {1 - x} \right)\left( {1 + x} \right) = 0.} \] Видно, что корни равны \({x_1} = - 1\), \({x_2} = 1.\) Используя метод интервалов, находим знаки производной в соответствующих интервалах (рисунок \(5\)). Таким образом, функция убывает (в строгом смысле) в интервалах \(\left( { - \infty , - 1} \right)\) и \(\left( {1, \infty} \right)\) и возрастает в промежутке \(\left( {-1, 1} \right).\) Учитывая, что корень функции равен \(x = 0,\) можно схематически нарисовать ее график (рисунок \(6\)).

   Пример 8

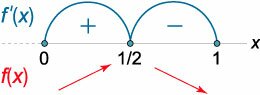
Найти интервалы монотонности функции \[f\left( x \right) = \frac{{\sqrt x }}{{x - 1}}\;\;\left( {x \ge 0} \right).\] Данная функция определена и дифференцируема при всех \(x \ge 0,\) кроме точки \(x = 1,\) где она имеет разрыв. Находим производную \(f'\left( x \right)\) и определяем интервалы знакопостоянства производной: \[ {f'\left( x \right) = {\left( {\frac{{\sqrt x }}{{x - 1}}} \right)^\prime } } = {\frac{{{{\left( {\sqrt x } \right)}^\prime }\left( {x - 1} \right) - \sqrt x {{\left( {x - 1} \right)}^\prime }}}{{{{\left( {x - 1} \right)}^2}}} } = {\frac{{\frac{1}{{2\sqrt x }} \cdot \left( {x - 1} \right) - \sqrt x \cdot 1}}{{{{\left( {x - 1} \right)}^2}}} } = {\frac{{x - 1 - 2x}}{{2\sqrt x {{\left( {x - 1} \right)}^2}}} } = { - \frac{{x + 1}}{{2\sqrt x {{\left( {x - 1} \right)}^2}}}.} \] Используя метод интервалов (рисунок \(7\)), устанавливаем, что производная всюду отрицательна, кроме точек \(x = 0\) и \(x = 1,\) где она не существует. Таким образом, функция строго убывает в интервалах \(\left( {0,1} \right)\) и \(\left( {1,\infty} \right).\) Ее схематический вид показан на рисунке \(8\).

   Пример 9

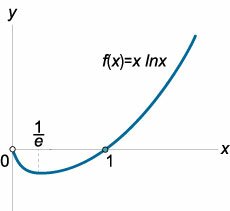
Найти интервалы монотонности функции \(f\left( x \right) = x\ln x.\) Функция определена и дифференцируема при \(x > 0.\) Ее производная равна \[ {f'\left( x \right) = {\left( {x\ln x} \right)^\prime } } = {x'\ln x + x{\left( {\ln x} \right)^\prime } } = {1 \cdot \ln x + x \cdot \frac{1}{x} } = {\ln x + 1.} \] Приравниваем производную нулю и находим интервалы ее знакопостоянства: \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow \ln x + 1 = 0,}\;\; {\Rightarrow \ln x = - 1,}\;\; {\Rightarrow \ln x = - \ln e,}\;\; {\Rightarrow \ln x = \ln \frac{1}{e},}\;\; {\Rightarrow x = \frac{1}{e}.} \] Решением строгого неравенства \(f'\left( x \right) > 0\) является бесконечный интервал \(x \in \left( {\large\frac{1}{e}\normalsize,\infty } \right)\) (рисунок 9), а решением неравенства \(f'\left( x \right) < 0\) − конечный интервал \(x \in \left( {0, \large\frac{1}{e}\normalsize} \right).\) Следовательно, на основании достаточного признака монотонности, функция строго возрастает при \(x \in \left( {\large\frac{1}{e}\normalsize,\infty } \right)\) и строго убывает при \(x \in \left( {0, \large\frac{1}{e}\normalsize} \right).\) Ее вид схематически приведен на рисунке \(10\).

   Пример 10

Найти интервалы монотонности функции \(f\left( x \right) = {x^2}{e^{ - x}}.\) Функция определена и дифференцируема на всей числовой прямой. Ее производная имеет вид: \[ {f'\left( x \right) = {\left( {{x^2}{e^{ - x}}} \right)^\prime } } = {{\left( {{x^2}} \right)^\prime }{e^{ - x}} + {x^2}{\left( {{e^{ - x}}} \right)^\prime } } = {2x{e^{ - x}} - {x^2}{e^{ - x}} } = {x{e^{ - x}}\left( {2 - x} \right).} \] Знаки производной легко определить методом интервалов (рисунок \(11\)). Как видно, \[ {f'\left( x \right) > 0\;\;\text{при}}\;\; {x \in \left( {0,2} \right);} \] \[ {f'\left( x \right) < 0\;\;\text{при}}\;\; {x \in \left( { - \infty ,0} \right) \cup \left( {2,\infty } \right).} \] На основании достаточного признака монотонности отсюда следует, что функция строго возрастает в интервале \(\left( {0,2} \right)\) и, соответственно, строго убывает в интервалах \(\left( {-\infty,0} \right)\) и \(\left( {2, \infty} \right).\) Ее схематический вид показан на рисунке \(12\).

   Пример 11

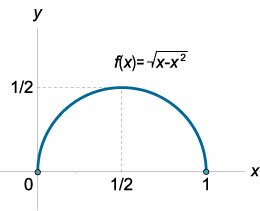
Найти интервалы монотонности функции \(f\left( x \right) = \sqrt {x - {x^2}}.\) Функция определена на следующем промежутке: \[ {x - {x^2} \ge 0,}\;\; {\Rightarrow x\left( {1 - x} \right) \ge 0,}\;\; {\Rightarrow x \in \left[ {0,1} \right].} \] Производная данной функции имеет вид: \[ {f'\left( x \right) = {\left( {\sqrt {x - {x^2}} } \right)^\prime } } = {\frac{1}{{2\sqrt {x - {x^2}} }} \cdot {\left( {x - {x^2}} \right)^\prime } } = {\frac{{1 - 2x}}{{2\sqrt {x - {x^2}} }}.} \] Следовательно, \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{1 - 2x}}{{2\sqrt {x - {x^2}} }} = 0,}\;\; {\Rightarrow x = \frac{1}{2}.} \] Исследуем знак производной (рисунок \(13\)). На основании достаточного признака монотонности заключаем, что функция возрастает при \(x \in \left( {0,\large\frac{1}{2}\normalsize} \right)\) и убывает при \(x \in \left( {\large\frac{1}{2}\normalsize,1} \right).\) График функции представляет собой полуокружность с центром в точке \(\left( {\large\frac{1}{2}\normalsize,0} \right)\) и радиусом \({\large\frac{1}{2}\normalsize}\) (рисунок \(14\)).

   Пример 12

Найти интервалы монотонности функции \(f\left( x \right) = \large\frac{{1 - \sin x}}{{\cos x}}\normalsize.\) Данная функция определена и дифференцируема при всех \(x \in \mathbb{R},\) кроме тех значений, в которых \(\cos x\) обращается в нуль, т.е. кроме \(x = \large\frac{\pi }{2}\normalsize + \pi n,\;n \in \mathbb{Z}.\) Найдем производную \(f'\left( x \right):\) \[ {f'\left( x \right) = {\left( {\frac{{1 - \sin x}}{{\cos x}}} \right)^\prime } } = {\frac{{{{\left( {1 - \sin x} \right)}^\prime }\cos x - \left( {1 - \sin x} \right){{\left( {\cos x} \right)}^\prime }}}{{{{\cos }^2}x}} } = {\frac{{ - {{\cos }^2}x - \left( {1 - \sin x} \right)\left( { - \sin x} \right)}}{{{{\cos }^2}x}} } = {\frac{{ - {{\cos }^2}x + \sin x - {{\sin }^2}x}}{{{{\cos }^2}x}} } = {\frac{{\sin x - 1}}{{{{\cos }^2}x}}.} \] Решим неравенство \(f'\left( x \right) \le 0:\) \[ {f'\left( x \right) \le 0,}\;\; {\Rightarrow \frac{{\sin x - 1}}{{{{\cos }^2}x}} \le 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\sin x - 1 \le 0}\\ {{{\cos }^2}x \ne 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\sin x \le 1}\\ {{{\cos }^2}x \ne 0} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {x \in \mathbb{R}}\\ {x \ne \frac{\pi }{2} + \pi n,\;n \in \mathbb{Z}} \end{array}} \right..} \] Таким образом, заданная функция убывает на всем множестве действительных чисел, исключая точки \(x = \large\frac{\pi }{2}\normalsize + \pi n,\;n \in \mathbb{Z},\) где она не определена.

   Пример 13

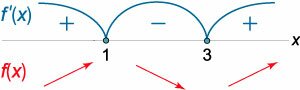
Найти все значения параметра \(a\), при которых функция \(f\left( x \right) = {x^3} - 6{x^2} + ax\) строго возрастает на всей области определения. Функция определена и дифференцируема на всей числовой прямой \(x \in \mathbb{R}.\) Ее производная имеет следующий вид: \[ {f'\left( x \right) = {\left( {{x^3} - 6{x^2} + ax} \right)^\prime } } = {3{x^2} - 12x + a.} \] Выделим в этом выражении полный квадрат: \[ {f'\left( x \right) = 3{x^2} - 12x + a } = {3{x^2} - 12x + 12 - 12 + a } = {3\left( {{x^2} - 4x + 4} \right) + a - 12 } = {3{\left( {x - 2} \right)^2} + a - 12.} \] Функция строго возрастает когда \(f'\left( x \right) \ge 0.\) Следовательно, условие строгого возрастания при всех \(x \in \mathbb{R}\) записывается как \[f'\left( x \right) = 3{\left( {x - 2} \right)^2} + a - 12 > 0.\] Очевидно, что производная принимает минимальное значение при \(x = 2.\) В этой точке она равна \[{f'_{\min }} = a - 12.\] Отсюда находим значения параметра \(a,\) при которых функция строго возрастает: \[a - 12 > 0\;\;\text{или}\;\;a > 12.\]

   Пример 14

Найти все значения параметра \(a\), при которых уравнение \({x^3} - 6{x^2} + 9x + a = 0\) имеет три различных действительных корня. Кубическая функция определена и дифференцируема на всей числовой прямой. Ее производная выражается формулой \[ {f'\left( x \right) = {\left( {{x^3} - 6{x^2} + 9x + a} \right)^\prime } } = {3{x^2} - 12x + 9.} \] Приравнивая производную нулю, определим промежутки монотонности функции (рисунок \(15\)): \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow 3{x^2} - 12x + 9 = 0,}\;\; {\Rightarrow {x^2} - 4x + 3 = 0,}\;\; {\Rightarrow {x_1} = 1,\;{x_2} = 3.} \] Итак, при переходе (слева направо) через точку \(x = 1\) возрастание функции сменяется ее убыванием, т.е. \(x = 1\) является точкой максимума функции. Аналогично, \(x = 3\) является точкой минимума функции. Кубическое уравнение будет иметь три различных действительных корня в случае, показанном на рисунке \(16\). Максимум функции должен принимать положительное значение, а минимум − отрицательное. Таким образом, мы приходим к следующему условию: \[\left\{ \begin{array}{l} y\left( 1 \right) > 0\\ y\left( 3 \right) < 0 \end{array} \right..\] Вычислим значения функции \(f\left( x \right)\) в указанных точках: \[ {y\left( 1 \right) = {1^3} - 6 \cdot {1^2} + 9 \cdot 1 + a } ={ a + 4,} \] \[y\left( 3 \right) = {3^3} - 6 \cdot {3^2} + 9 \cdot 3 + a = a.\] Теперь легко найти интервал значений параметра \(a:\) \[ {\left\{ \begin{array}{l} y\left( 1 \right) > 0\\ y\left( 3 \right) < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} a + 4 > 0\\ a < 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} a > - 4\\ a < 0 \end{array} \right.,}\;\; {\Rightarrow a \in \left( { - 4,0} \right).} \]

   Пример 15

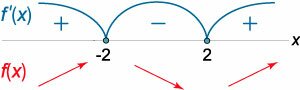
Определить число корней кубического уравнения \({x^3} - 12x + a = 0\) в зависимости от параметра \(a.\) Функция в левой части уравнения определена и дифференцируема на все числовой прямой. Производная функции имеет вид: \[ {f'\left( x \right) = {\left( {{x^3} - 12x + a} \right)^\prime } } = {3{x^2} - 12.} \] Вычислим корни производной: \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow 3{x^2} - 12 = 0,}\;\; {\Rightarrow 3\left( {{x^2} - 4} \right) = 0,}\;\; {\Rightarrow {x_1} = - 2,\;{x_2} = 2.} \] При переходе слева направо через точку \({x_1} = - 2\) производная меняет знак с "\(+\)" на "\(-\)" (рисунок \(17\)). Поэтому точка \({x_1}\) является точкой максимума. Аналогично устанавливаем, что точка \({x_2} = 2\) является точкой минимума.

Запишем значения функции в указанных точках: \[ {{f_{\max }} = f\left( { - 2} \right) } = {{\left( { - 2} \right)^3} - 12 \cdot \left( { - 2} \right) + a } = { - 8 + 24 + a } = {a + 16,} \] \[ {{f_{\min }} = f\left( 2 \right) } = {{2^3} - 12 \cdot 2 + a } = {8 - 24 + a } = {a - 16.} \] Уравнение имеет один корень, если точки максимума и минимума расположены в одной (верхней или нижней) полуплоскости, как показано на рисунке \(18\). Такая конфигурация описывается условием \({f_{\max }} \cdot {f_{\min }} > 0.\) Решая это неравенство, получаем: \[ {{f_{\max }} \cdot {f_{\min }} > 0,}\;\; {\Rightarrow \left( {a + 16} \right)\left( {a - 16} \right) > 0,}\;\; {\Rightarrow {a^2} - {16^2} > 0,}\;\; {\Rightarrow {a^2} > {16^2},}\;\; {\Rightarrow \left| a \right| > 16.} \] Теперь рассмотрим случай, когда уравнение имеет \(2\) корня. Возможное расположение графика функции для этого случая приведено на рисунке \(19\). Поскольку один из корней совпадает с точкой максимума или минимума, то соответствующее условие записывается в виде: \[ {{f_{\max }} \cdot {f_{\min }} = 0,}\;\; {\Rightarrow \left( {a + 16} \right)\left( {a - 16} \right) = 0,}\;\; {\Rightarrow a = \pm 16,}\;\; {\Rightarrow \left| a \right| = 16.} \] Наконец, уравнение имеет три различных корня, если точки максимума и минимума расположены в разных полуплоскостях (рис.\(20\)). Следовательно, здесь мы имеем: \[ {{f_{\max }} \cdot {f_{\min }} < 0,}\;\; {\Rightarrow \left( {a + 16} \right)\left( {a - 16} \right) < 0,}\;\; {\Rightarrow {a^2} - {16^2} < 0,}\;\; {\Rightarrow {a^2} < {16^2},}\;\; {\Rightarrow \left| a \right| < 16.} \] Собирая вместе эти результаты, запишем окончательный ответ:

Данное кубическое уравнение имеет один корень при \(\left| a \right| > 16,\) два корня при \(\left| a \right| = 16\) и три корня при \(\left| a \right| < 16.\)