|
Механические колебания
|
||||||||||||||||||
|
Колебательные процессы встречаются повсюду в природе и технике. В астрономии планеты периодически обращаются вокруг Солнца, переменные звезды, такие как цефеиды, периодически меняют свою яркость, движение Луны вызывает приливы и отливы. В геофизике периодические процессы проявляются при изменении климата, в поведении океанических течений, в динамике циклонов и антициклонов. Внутри живых организмов происходят десятки различных периодических процессов с периодом от доли секунды до года, и т.д.
Мы начнем рассмотрение колебаний с анализа простейшей системы − гармонического осциллятора.
Свободные гармонические колебания
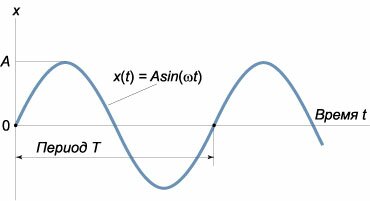
Примером такой простейшей системы является груз массы \(m,\) прикрепленный к пружине жесткостью \(k\) (рисунок \(1\)). В идеальном случае (пренебрегая сопротивлением воздуха и внутренним трением) такая система будет совершать незатухающие гармонические колебания, при которых смещение \(x\) описывается функцией косинус или синус: \[x\left( t \right) = A\cos \left( {\omega t + {\varphi _0}} \right)\;\;\text{или}\;\;x\left( t \right) = A\sin \left( {\omega t + {\varphi _0}} \right).\] В этих формулах \(A\) означает амплитуду колебаний, \({\omega t + {\varphi _0}}\) − фазу колебаний, \({{\varphi _0}}\) − начальную фазу в момент \(t = 0.\) Величина \(\omega\) называется круговой или циклической частотой колебаний. Она связана с периодом колебаний \(T\) соотношением \[\omega = \frac{{2\pi }}{T}.\]
В случае груза на пружинке, возвращающая сила при малых колебаниях подчиняется закону Гука: \[F = - kx,\] где \(k\) − жесткость пружины. Здесь координата \(x = 0\) соответствует точке равновесия, в которой сила тяжести скомпенсирована начальным растяжением пружины. Тогда, согласно второму закону Ньютона, движение груза будет описываться дифференциальным уравнением \[mx'' = - kx,\;\; \Rightarrow x'' + \frac{k}{m}x = 0.\] Таким образом, грузик будет совершать незатухающие гармонические колебания с круговой частотой \[\omega = \sqrt {\frac{k}{m}} .\] Период колебаний, соответственно, будет равен \[T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} .\] Аналогичный анализ другой колебательной системы − математического маятника − приводит к следующей формуле для периода колебаний: \[T = 2\pi \sqrt {\frac{L}{g}} ,\] где \(L\) − длина маятника, \(g\) − ускорение свободного падения. В случае физического маятника период колебаний определяется выражением \[T = 2\pi \sqrt {\frac{I}{{mga}}} ,\] где \(I\) − момент инерции тела относительно оси вращения, \(m\) − масса тела, \(a\) − расстояние от оси вращения до центра масс.
Затухающие колебания
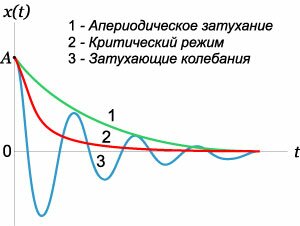
В реальных колебательных системах всегда присутствуют силы трения или сопротивления, которые приводят к постепенному затуханию колебаний. Во многих случаях сила сопротивления (обозначим ее \({F_\text{C}}\)) пропорциональна скорости движения тела, т.е. \[{F_\text{C}} = - cx'.\] Тогда в случае груза на пружинке при учете силы сопротивления дифференциальное уравнение будет записываться в виде \[ {mx'' + cx' + kx = 0,}\;\; {\Rightarrow x'' + \frac{c}{m}x' + \frac{k}{m}x = 0.} \] Введем обозначения: \({\large\frac{c}{m}\normalsize} = 2\beta,\) \({\large\frac{k}{m}\normalsize} = \omega_0^2.\) Здесь \({\omega_0}\) − собственная частота колебаний незатухающего осциллятора (ранее мы обозначали ее как \(\omega\)), \(\beta\) − коэффициент затухания. В новых обозначениях дифференциальное уравнение выглядит так: \[x'' + 2\beta x' + \omega _0^2x = 0.\] Будем искать решение этого уравнения в виде функции \[x\left( t \right) = A{e^{\lambda t}}.\] Производные, соответственно, равны \[ {x'\left( t \right) = A\lambda {e^{\lambda t}},}\;\; {x''\left( t \right) = A{\lambda ^2}{e^{\lambda t}}.} \] Подставляя это в дифференциальное уравнение, получаем алгебраическое характеристическое уравнение: \[ {A{\lambda ^2}{e^{\lambda t}} + 2\beta A\lambda {e^{\lambda t}} + \omega _0^2A{e^{\lambda t}} = 0,}\;\; {\Rightarrow {\lambda ^2} + 2\beta \lambda + \omega _0^2 = 0.} \] Это уравнение имеет следующие корни: \[ {D = 4{\beta ^2} - 4\omega _0^2,}\;\; {\Rightarrow {\lambda _{1,2}} = \frac{{ - 2\beta \pm \sqrt {4{\beta ^2} - 4\omega _0^2} }}{2} = - \beta \pm \sqrt {{\beta ^2} - \omega _0^2} .} \] Видно, что в зависимости от знака подкоренного выражения \({{\beta ^2} - \omega _0^2}\) могут возникнуть три различных типа решения.
Случай 1. Режим апериодического затухания: \(\beta > {\omega _0}\)
В этом случае (при сильном затухании) подкоренное выражение положительно: \({{\beta ^2} \gt \omega _0^2}.\) Корни характеристического уравнения действительны и отрицательны. Общее решение дифференциального уравнения имеет вид \[x\left( t \right) = {C_1}{e^{{\lambda _1}t}} + {C_2}{e^{{\lambda _2}t}},\] где коэффициенты \({C_1},{C_2},\) как обычно, зависят от начальных условий. Из полученного выражения следует, что в системе отсутствуют колебания и возврат к равновесному состоянию происходит по экспоненциальному закону, т.е. апериодически (рисунок \(3\)).
Случай 2. Граничный режим: \(\beta = {\omega _0}\)
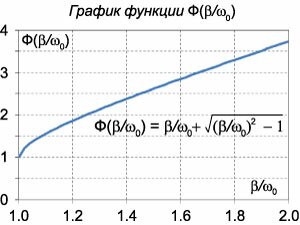
В предельном случае, при \(\beta = {\omega _0},\) корни характеристического уравнения будут совпадающими и действительными: \[{\lambda _1} = {\lambda _2} = - \beta = - {\omega _0}.\] Здесь решение будет определяться формулой \[x\left( t \right) = \left( {{C_1}t + {C_2}} \right){e^{ - {\omega _0}t}}.\] В этом режиме величина \(x\left( t \right)\) может даже возрастать в начале процесса из-за действия линейного множителя \({{C_1}t + {C_2}}.\) Но в итоге отклонение \(x\left( t \right)\) быстро уменьшается вследствие экспоненциального затухания с характерным временем \(\tau = \large\frac{{2\pi }}{{{\omega _0}}}\normalsize.\) Заметим, что в граничном режиме релаксация происходит быстрее, чем в случае апериодического затухания. Действительно, в апериодическом режиме время релаксации будет определяться меньшим (по абсолютной величине) корнем \({\lambda_1}\) и будет составлять \[\require{cancel} {\tau = \frac{{2\pi }}{{{\lambda _1}}} } = {\frac{{2\pi }}{{\beta - \sqrt {{\beta ^2} - \omega _0^2} }} } = {\frac{{2\pi \left( {\beta + \sqrt {{\beta ^2} - \omega _0^2} } \right)}}{{\left( {\beta - \sqrt {{\beta ^2} - \omega _0^2} } \right)\left( {\beta + \sqrt {{\beta ^2} - \omega _0^2} } \right)}} } = {\frac{{2\pi \left( {\beta + \sqrt {{\beta ^2} - \omega _0^2} } \right)}}{{\cancel{\beta ^2} - \cancel{\beta ^2} + \omega _0^2}} } = {\frac{{2\pi }}{{{\omega _0}}}\left[ {\frac{\beta }{{{\omega _0}}} + \sqrt {{{\left( {\frac{\beta }{{{\omega _0}}}} \right)}^2} - 1} } \right] } = {\frac{{2\pi }}{{{\omega _0}}}\Phi \left( {\frac{\beta }{{{\omega _0}}}} \right).} \] Входящая в это выражение функция \(\Phi \left( {\large\frac{\beta }{{{\omega _0}}}\normalsize} \right)\) является монотонно возрастающей и всегда больше или равна \(1,\) как видно из рисунка \(4.\) В рассматриваемом граничном случае (случай \(2\)) отношение \({\large\frac{\beta }{{{\omega _0}}}\normalsize} = 1,\) а в случае апериодического затухания (случай \(1\)) \({\large\frac{\beta }{{{\omega _0}}}\normalsize} \gt 1.\) Поэтому для апериодического режима затухания справедливо соотношение \[\tau = \frac{{2\pi }}{{{\omega _0}}}\Phi \left( {\frac{\beta }{{{\omega _0}}}} \right) > \frac{{2\pi }}{{{\omega _0}}}.\] Таким образом, граничный или критический режим релаксации обеспечивает максимально быстрый возврат системы в равновесное состояние. Конструкции такого типа используются, например, при закрывании дверей.
Случай 3. Режим малого затухания: \(\beta < {\omega _0}\)
Здесь корни характеристического уравнения являются комплексно-сопряженными: \[{\lambda _{1,2}} = - \beta \pm i\sqrt {\omega _0^2 - {\beta ^2}} .\] Общее решение дифференциального уравнения имеет колебательный характер и записывается как \[x\left( t \right) = {e^{ - \beta t}}\left[ {{C_1}\cos \left( {{\omega _1}t} \right) + {C_2}\sin\left( {{\omega _1}t} \right)} \right],\] где частота колебаний \({\omega_1}\) равна \[{\omega _1} = \sqrt {\omega _0^2 - {\beta ^2}} .\] Полученную формулу можно записать в несколько другом виде: \[x\left( t \right) = A{e^{ - \beta t}}\cos \left( {{\omega _1}t + {\varphi _0}} \right),\] где \({\varphi_0}\) − начальная фаза колебаний и \(A\cos {\varphi _0}\) − начальная амплитуда колебаний. Видно, что в этом режиме происходят классические затухающие колебания. При этом частота колебаний \({\omega_1}\) меньше гармонической частоты \({\omega_0},\) а амплитуда колебаний уменьшается по экспоненциальному закону \({e^{ - \beta t}}.\)
Вынужденные колебания. Резонанс
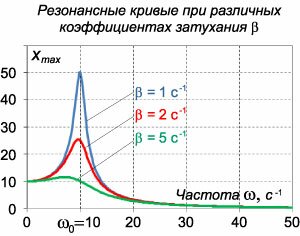
Пусть на колебательную систему действует внешняя сила, изменяющаяся со временем по гармоническому закону с частотой \(\omega:\) \[F\left( t \right) = {F_0}\cos \left( {\omega t} \right).\] В случае незатухающего осциллятора из второго закона Ньютона вытекает дифференциальное уравнение вида \[x'' + \omega _0^2x = \frac{{{F_0}}}{m}\cos \left( {\omega t} \right).\] В соответствии с общей теорией, решением данного уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного уравнения.Общее решение однородного уравнения было уже получено выше. Оно записывается в виде \[{x_0}\left( t \right) = A\sin \left( {{\omega _0}t + {\varphi _0}} \right),\] где амплитуда \(A\) и фаза \({\varphi _0}\) определяются начальными условиями. Найдем частное решение неоднородного дифференциального уравнения. Будем искать его в виде \[{x_1}\left( t \right) = B\cos \left( {\omega t} \right).\] Производные этой функции равны \[ {{x'_1}\left( t \right) = - B\omega \sin \left( {\omega t} \right),}\;\; {{x''_1}\left( t \right) = - B{\omega ^2}\cos\left( {\omega t} \right).} \] После подстановки в дифференциальное уравнение получаем \[ {- B{\omega ^2}\cos\left( {\omega t} \right) + \omega _0^2B\cos\left( {\omega t} \right) = \frac{{{F_0}}}{m}\cos\left( {\omega t} \right),}\;\; {\Rightarrow - B{\omega ^2} + \omega _0^2B = \frac{{{F_0}}}{m},}\;\; {\Rightarrow B = \frac{{{F_0}}}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}.} \] Следовательно, общее решение неоднородного уравнения записывается в виде \[ {x\left( t \right) = {x_0}\left( t \right) + {x_1}\left( t \right) } = {A\sin \left( {{\omega _0}t + {\varphi _0}} \right) + \frac{{{F_0}}}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}\cos \left( {\omega t} \right).} \] Из этого выражения видно, что второе слагаемое, показывающее влияние вынужденной силы, резко возрастает при \(\omega \to {\omega _0}.\) Указанное явление называется резонансом. В данной простой модели амплитуда колебаний \(x\left( t \right)\) становится равной бесконечности, если частота вынужденной силы равна частоте свободных колебаний системы. Физическая модель вынужденных колебаний получается более реалистичной, если учесть затухание колебаний. Тогда из второго закона Ньютона вытекает следующее дифференциальное уравнение: \[x'' + 2\beta x' + \omega _0^2x = \frac{{{F_0}}}{m}\cos \left( {\omega t} \right).\] Решение этого уравнения также будет представляться в виде суммы общего решения однородного уравнения и частного решения неоднородного уравнения. Решение однородного уравнения, как показано выше, включает в себя три возможных сценария (режим апериодического затухания, граничный режим и колебательное решение в случае малого затухания). Определим частное решение неоднородного уравнения. Здесь удобнее перейти к комплексной форме дифференциального уравнения, которое запишется как \[x'' + 2\beta x' + \omega _0^2x = \frac{{{F_0}}}{m}{e^{i\omega t}}.\] Будем искать частное решение в виде \[{x_1}\left( t \right) = B{e^{i\left( {\omega t + \varphi } \right)}},\] то есть предположим, что колебания в системе будут происходить с частотой внешней силы \(\omega\) и, возможно, с некоторым сдвигом \(\varphi.\) В результате имеем \[ {{x'_1}\left( t \right) = i\omega B{e^{i\left( {\omega t + \varphi } \right)}},}\;\; {{x''_1}\left( t \right) = - {\omega ^2}B{e^{i\left( {\omega t + \varphi } \right)}}.} \] Подставляя это в дифференциальное уравнение, получаем \[ {- {\omega ^2}B{e^{i\left( {\omega t + \varphi } \right)}} + 2\beta i\omega B{e^{i\left( {\omega t + \varphi } \right)}} + \omega _0^2B{e^{i\left( {\omega t + \varphi } \right)}} } = {\frac{{{F_0}}}{m}{e^{i\omega t}},} \] \[ \Rightarrow \left( { - {\omega ^2} + 2i\beta \omega + \omega _0^2} \right)B\cancel{e^{i\omega t}}{e^{i\varphi }} = \frac{{{F_0}}}{m}\cancel{e^{i\omega t }},\] \[ \Rightarrow \left( {\omega _0^2 - {\omega ^2}} \right)B + 2i\beta \omega B = \frac{{{F_0}}}{m}{e^{ - i\varphi }}.\] По формуле Муавра-Лапласа \[{e^{ - i\varphi }} = \cos \varphi - i\sin\varphi .\] Поэтому можно записать: \[\left( {\omega _0^2 - {\omega ^2}} \right)B + 2i\beta \omega B = \frac{{{F_0}}}{m}\left( {\cos \varphi - i\sin\varphi } \right).\] Приравнивая отдельно действительную и мнимую части, получаем \[\left\{ \begin{array}{l} \left( {\omega _0^2 - {\omega ^2}} \right)B = \frac{{{F_0}}}{m}\cos \varphi \\ 2\beta \omega B = \frac{{{F_0}}}{m}\sin\varphi \end{array} \right..\] Из этой системы уравнений мы определим коэффициент \(B\) и угол \(\varphi.\) Возводя обе части в квадрат и складывая, находим: \[ {{B^2}\left[ {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} \right] = {\left( {\frac{{{F_0}}}{m}} \right)^2},}\;\; {\Rightarrow B = \frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}.} \] Угол \(\varphi\) найдем, разделив второе уравнение на первое: \[ {\frac{{2\beta \omega }}{{\omega _0^2 - {\omega ^2}}} = \frac{{\sin \varphi }}{{\cos\varphi }} = \tan \varphi ,}\;\; {\Rightarrow \varphi = \arctan \frac{{2\beta \omega }}{{\omega _0^2 - {\omega ^2}}}.} \] Итак, частное решение неоднородного уравнения в комплексной форме имеет вид \[{x_1}\left( t \right) = \frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}{e^{i\left( {\omega t + \varphi } \right)}},\] где угол сдвига \(\varphi\) вычисляется по полученной выше формуле. Соответственно, действительная часть решения записывается как \[ {\text{Re}\left[ {{x_1}\left( t \right)} \right] } = {\frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}\cos\left[ {i\left( {\omega t + \varphi } \right)} \right].} \] Окончательный ответ представляет собой сумму двух членов: \[ {x\left( t \right) = {x_0}\left( t \right) + \text{Re}\left[ {{x_1}\left( t \right)} \right] } = {{x_0}\left( t \right) + \frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}\cos\left[ {i\left( {\omega t + \varphi } \right)} \right],} \] где \({x_0}\left( t \right)\) − общее решение однородного уравнения, описывающего осциллятор с затуханием без действия вынужденной силы. Заметим, что вследствие затухания решение однородного уравнения \({x_0}\left( t \right)\) будет стремиться к нулю. Поэтому в установившемся режиме характер колебаний будет зависеть лишь от вынужденной силы, то есть будет определяться вторым компонентом общего решения: \[x\left( t \right) = \frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}\cos\left[ {i\left( {\omega t + \varphi } \right)} \right],\] где \(\varphi = \arctan \large\frac{{2\beta \omega }}{{\omega _0^2 - {\omega ^2}}}\normalsize,\) \(\beta\) − коэффициент затухания. Эта формула описывает также и явление резонанса, причем максимальная амплитуда установившихся колебаний при резонансе будет конечной и равной \[{x_{\max }}\left( {\omega = {\omega _0}} \right) = \frac{{{F_0}}}{{2m\beta {\omega_0} }}.\] Зависимость амплитуды установившихся колебаний \({x_{\max }}\) от частоты вынужденной силы \(\omega\) вблизи резонананса при различных коэффициентах затухания \(\beta\) показана ниже на рисунке \(5.\) Такие кривые называются резонансными кривыми. Для оценки свойств колебательной системы в окрестности резонанса используют понятие добротности. Добротность показывает во сколько раз амплитуда вынужденных колебаний при резонансе превышает их амплитуду вдали от резонанса. При стремлении частоты вынужденной силы \(\omega\) к нулю амплитуда колебаний механической системы приближается к \(\large\frac{{{F_0}}}{{m\omega _0^2}}\normalsize :\) \[ {\lim\limits_{\omega \to 0} {x_{\max }} } = {\lim\limits_{\omega \to 0} \frac{{{F_0}}}{{m\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }} = \frac{{{F_0}}}{{m\omega _0^2}}} \] Поэтому добротность механической колебательной системы будет равна \[ {Q = \frac{{{x_{\max }}\left( {\omega = {\omega _0}} \right)}}{{{x_{\max }}\left( {\omega \to 0} \right)}} } = {\frac{{\frac{{{F_0}}}{{2m\beta {\omega _0}}}}}{{\frac{{{F_0}}}{{m\omega _0^2}}}} } = {\frac{{{\omega _0}}}{{2\beta }},} \] где \(\beta\) − коэффициент затухания. Добротность является очень полезной характеристикой. С энергетической точки зрения она показывает отношение энергии, запасенной в колебательной системе, к энергии, которую система теряет за один период колебаний. Потери энергии характеризуются также логарифмическим декрементом затухания \(\delta.\) Соотношение между добротностью \(Q\) и логарифмическим декрементом затухания \(\delta\) (при малых \(\delta\)) выражается простой формулой: \[Q = \frac{\pi }{\delta }.\]
|
||||||||||||||||||
|
Пример 1
|
||||||||||||||||||
|
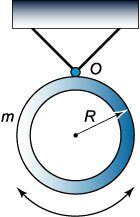
Кольцо радиуса \(R\) совершает малые колебания вокруг точки подвеса \(O\) (рисунок \(6\)). Определить период колебаний.
Решение. Момент инерции кольца массой \(m\) равен \({I_0} = m{R^2}.\) Поскольку расстояние от центра кольца до точки подвеса равно \(R.\) то по теореме Штейнера-Гюйгенса полный момент инерции маятника равен \[I = {I_0} + m{R^2} = m{R^2} + m{R^2} = 2m{R^2}.\] Учитывая, что \(a = R,\) получаем следующее выражение для периода колебаний: \[ {T = 2\pi \sqrt {\frac{I}{{mga}}} = 2\pi \sqrt {\frac{{2\cancel{m}{R^{\cancel{2}}}}}{{\cancel{m}g\cancel{R}}}} } = {2\pi \sqrt {\frac{{2R}}{g}} .} \] |
||||||||||||||||||
|
Пример 2
|
||||||||||||||||||
|
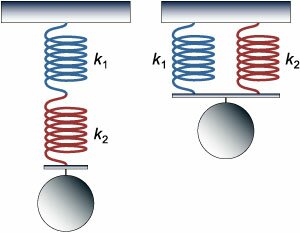
Груз подвешен на двух последовательно соединенных пружинах. Жесткость одной пружины в два раза больше жесткости другой: \({k_2} = 2{k_1}.\) Как изменится период колебаний, если пружины соединить параллельно (рисунок \(7\))?
Решение.
Вычислим эквивалентную жесткость в случае последовательного и параллельного соединения пружин.В случае последовательного соединения сила упругости в каждой пружине равна силе тяжести (без учета веса самих пружин). Общее удлинение равно сумме удлинений каждой пружины: \[x = {x_1} + {x_2}.\] Тогда эквивалентная жесткость равна \[ {x = {x_1} + {x_2},}\;\; {\Rightarrow \frac{F}{k} = \frac{F}{{{k_1}}} + \frac{F}{{{k_2}}},}\;\; {\Rightarrow \frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}},}\;\; {\Rightarrow k = \frac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}.} \] При параллельном соединении удлинение обеих пружин будет одинаковым, а полная сила упругости будет равна сумме сил, действующих в каждой пружине: \[x = {x_1} = {x_2},\;\;F = {F_1} + {F_2}.\] Отсюда находим эквивалентную жесткость для параллельно соединенных пружин: \[ {F = {F_1} + {F_2},}\;\; {\Rightarrow kx = {k_1}{x_1} + {k_2}{x_2} = \left( {{k_1} + {k_2}} \right)x,}\;\; {\Rightarrow k = {k_1} + {k_2}.} \] Таким образом, период колебаний при последовательном соединении пружин равен \[{T_1} = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{m\left( {{k_1} + {k_2}} \right)}}{{{k_1}{k_2}}}} ,\] а в случае параллельного соединения: \[{T_2} = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{m}{{{k_1} + {k_2}}}} .\] Отсюда находим как изменится период колебаний при переходе от последовательного к параллельному соединению пружин: \[\frac{{{T_2}}}{{{T_1}}} = \frac{{\sqrt {\frac{1}{{{k_1} + {k_2}}}} }}{{\sqrt {\frac{{{k_1} + {k_2}}}{{{k_1}{k_2}}}} }} = \frac{{\sqrt {{k_1}{k_2}} }}{{{k_1} + {k_2}}}.\] Учитывая, что жесткость одной пружины в два раза больше жесткости другой, получаем: \[ {\frac{{{T_2}}}{{{T_1}}} = \frac{{\sqrt {{k_1}{k_2}} }}{{{k_1} + {k_2}}} } = {\frac{{\sqrt {2k_1^2} }}{{{k_1} + 2{k_1}}} } = {\frac{{\sqrt 2 \cancel{k_1}}}{{3\cancel{k_1}}} } = {\frac{{\sqrt 2 }}{3}.} \] |
||||||||||||||||||
|
Пример 3
|
||||||||||||||||||
|
Найти добротность осциллятора,если через \(50\) колебаний амплитуда смещения уменьшилась в \(2\) раза.
Решение. |
||||||||||||||||||